valószínűség és statisztika > regressziós analízis > szabványosított béta-együttható

mi a standardizált béta-együttható?

egy szabványosított béta-együttható összehasonlítja az egyes független változók hatásának erősségét a függő változóval. Minél magasabb a béta-együttható abszolút értéke, annál erősebb a hatás. Például egy béta -.A 9-nek erősebb hatása van, mint a +béta.8. Szabványosított béta együtthatók standard eltérések, mint azok egység. Ez azt jelenti, hogy a változók könnyen összehasonlíthatók egymással. Más szavakkal, a szabványosított béta-együtthatók azok az együtthatók, amelyeket akkor kapna, ha a regresszió változóit az elemzés futtatása előtt mind z-pontszámra konvertálták.

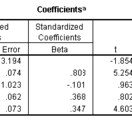
béták az SPSS kimeneten.

a regressziós analízis során gyakran használnak különböző egységeket és különböző skálákat. Például az egyik változó dollárokat, a másik százalékokat használhat. Az együtthatók szabványosítása azt jelenti, hogy összehasonlíthatja az egyes együtthatók relatív fontosságát egy regressziós modellben.

tegyük fel például, hogy a modellben benne van, hogy a szülők jövedelme és az iskolai végzettségük milyen hatással volt utódaik élethosszig tartó jövedelmére. A szülők jövedelmét dollárban mérik, az oktatási szintet pedig az iskolai években mérik. Ezeknek a változóknak a szabványosítása azt jelenti, hogy összehasonlíthatók egymással a modellben. Tegyük fel, hogy a jövedelem standardizált béta-együtthatóval rendelkezik .2 az oktatási szint béta .34. A modell azt mutatja, hogy a szülő jövedelmének egy szórásának minden növekedésével az utódok jövedelme növekszik .2 szórás. Ez feltételezi, hogy a másik változó (oktatási szint) állandó. Az oktatási szint egy szórásának növekedésével a jövedelem emelkedik .34 szórás – feltételezve, hogy a szülő jövedelme állandó.

a név ellenére valójában nem a szabványosított együtthatók, hanem a változók. A bétákat úgy számítják ki, hogy kivonják az átlagot a változóból, és elosztják annak szórásával. Ez azt eredményezi, hogy a standardizált változók átlaga nulla, szórása pedig 1.

standardizált béta-együtthatókat is neveznek:

• Betas.
• béta együtthatók.
• béta súlyok.
• standardizált együtthatók.

Agresti A. (1990) kategorikus Adatelemzés. John Wiley és Sons, New York.
Dodge, Y. (2008). A statisztikák Tömör enciklopédiája. Springer.
Everitt, B. S.; Skrondal, A. (2010), the Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum könnyű statisztikai vázlata, második kiadás (Schaum könnyű körvonalai) 2.kiadás. McGraw-Hill Education

——————————————————————————

segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg tanulmány segítségével lépésről-lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!