Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Bevezetés
a Négyzetgyökeket leggyakrabban radikális jelzéssel írják, mint ez, ![]() . De van egy másik módja annak, hogy képviselje a gyökeret. A radikális helyett racionális exponenseket használhat. A racionális exponens egy kitevő, amely egy frakció. Például
. De van egy másik módja annak, hogy képviselje a gyökeret. A radikális helyett racionális exponenseket használhat. A racionális exponens egy kitevő, amely egy frakció. Például ![]() lehet írni, mint
lehet írni, mint ![]() .
.
nem tudja elképzelni, hogy egy számot racionális exponensre emeljen? Lehet, hogy nehéz megszokni, de a racionális exponensek valóban segíthetnek egyes problémák egyszerűsítésében. Vizsgáljuk meg a racionális (frakcionált) exponensek és a radikálisok kapcsolatát.
radikális kifejezések átírása racionális Exponensekkel
a gyökök és a frakcionált exponensek alternatív módon fejezik ki ugyanazt. Már láttad, hogy a négyzetgyökerek hogyan fejezhetők ki exponensként a fele erejéig.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Ne feledje, hogy egy szám megragadása három erejéig emeli. Figyeljük meg, hogy ezekben a példákban a racionális exponens nevezője a 3. szám.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and racionális exponensek: nevezetesen, hogy egy szám n-edik gyökere lehet ![]() vagy
vagy ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an kifejezés, amely egy racionális exponens, akkor átírni egy radikális. A fenti táblázatban vegye figyelembe, hogy a racionális exponens nevezője hogyan határozza meg a gyökér indexét. Tehát a ![]() exponens a négyzetgyökre fordul, a
exponens a négyzetgyökre fordul, a ![]() exponens az ötödik gyökérre vagy
exponens az ötödik gyökérre vagy ![]() fordítja, és
fordítja, és ![]() fordítja a nyolcadik gyökérre vagy
fordítja a nyolcadik gyökérre vagy ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
írja át a kifejezést a frakcionált exponenssel radikálisként. A frakció nevezője határozza meg a gyökeret, ebben az esetben a kocka gyökerét. a |
|
|
Válasz |
|
|
ne feledje, hogy kitevőkkel csak azokra a mennyiséget, azonnal, hogy a bal, kivéve, ha az egyesülés szimbólum. Az alábbi példa nagyon hasonlít az előző példához, egy fontos különbséggel-nincsenek zárójelek! Nézd, mi történik.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. A frakció nevezője határozza meg a gyökeret, ebben az esetben a kocka gyökerét. az exponens csak a kifejezés azon részére vonatkozik, amely közvetlenül az exponens bal oldalán található, ebben az esetben x, de nem a 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. Ebben az esetben a radikális index 3, így a racionális exponens mivel a 4 a radikálison kívül esik, nem szerepel a csoportosítási szimbólumban, és az exponens nem hivatkozik rá. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
|
||
p> a fenti példákban szereplő frakcionált exponensek összes számlálója 1 volt. Használhatja frakcionált exponensek, amelyek számlálók eltérő 1 kifejezni gyökerek, az alábbiak szerint. Észrevett valami mintát a táblán belül?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
a radikális frakcionált exponens használatával történő átírásához a radicand felemelkedésének ereje lesz a számláló, a gyökér pedig a nevező.
frakcionált exponensek írása
bármely radikális formában ![]() frakcionált exponens segítségével írható
frakcionált exponens segítségével írható ![]() formában.
formában.
a![]() és
és![]() racionális exponensek esetében működik, amelyek számlálója is 1. Például a radikális
racionális exponensek esetében működik, amelyek számlálója is 1. Például a radikális ![]()
![]() is írható, mivel bármely szám ugyanaz az érték marad, ha az első teljesítményre emelkedik. Most már láthatja, honnan származik az 1 számlálója a
is írható, mivel bármely szám ugyanaz az érték marad, ha az első teljesítményre emelkedik. Most már láthatja, honnan származik az 1 számlálója a ![]() egyenértékű formában.
egyenértékű formában.
radikális kifejezések egyszerűsítése racionális exponensek és az exponensek törvényei segítségével
vizsgáljuk meg néhány radikális kifejezést most, és nézzük meg, hogyan lehet egyszerűsíteni őket. Itt van egy radikális kifejezés, amelyet egyszerűsíteni kell, ![]() .
.
ennek a kifejezésnek az egyszerűsítésének egyik módja az A3 csoportjainak faktorálása és kihúzása, amint azt az alábbi példa mutatja.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
Válasz |
|
|
Azt is egyszerűsíteni ez a kifejezés a gondolkodás arról, hogy a radikális, mint egy mondás, hogy egy racionális kitevő, felhasználva azt az elvet, hogy minden radikális formában ![]() lehet írni segítségével tört kitevő formájában
lehet írni segítségével tört kitevő formájában ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
mindkét egyszerűsítési módszer ugyanazt az eredményt adta, a2. A probléma kontextusától függően könnyebb lehet az egyik vagy a másik módszer használata, de most megjegyezzük, hogy ezt a kifejezést gyorsabban egyszerűsítheti racionális exponensek segítségével, mint a “kihúzás” módszer használatakor.
próbáljunk ki egy másik példát.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the racionális exponens vissza radikális formában. |
|
|
válasz |
|
|
ismét az alternatív módszer a radikális egyszerűsítés a faktoring használatával. Az éppen megoldott példánál ez így néz ki.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
próbáljunk ki egy bonyolultabb kifejezést, ![]() . Ennek a kifejezésnek két változója van, egy töredéke és egy radikális. Vegyük lépésről lépésre, és nézzük meg, hogy a frakcionált exponensek használata segíthet-e egyszerűsíteni.
. Ennek a kifejezésnek két változója van, egy töredéke és egy radikális. Vegyük lépésről lépésre, és nézzük meg, hogy a frakcionált exponensek használata segíthet-e egyszerűsíteni.
kezdjük a nevező egyszerűsítésével, mivel itt található a radikális jel.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Egyezmény szerint a kifejezést általában nem tekintik egyszerűsítettnek, ha frakcionált exponens vagy radikális a nevezőben. |
||
|
válasz |
|
||
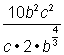
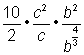
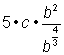
Leave a Reply