egy erő egy adott irányba tolható vagy tolható. Ha egy objektumra erőt alkalmazunk,az objektum mozgása attól függ, hogy az adott objektum hol helyezkedik el, és hogyan korlátozódik az objektum.Ha az objektum nincs meghatározva, és az erő a gravitáció középpontján keresztül kerül alkalmazásra,az objektum tiszta fordításban mozog, amint azt Newton mozgástörvényei leírják.Ha az objektum az apivot nevű helyen van korlátozva (vagy rögzítve), akkor az objectrotatesabout a pivot, de nem fordítja le.Az erőt a forgócsapon keresztül továbbítjákés a forgatás részletei a távolságtól függnekaz alkalmazott erő a forgócsaphoz.Ha az objektum nincs meghatározva, és az erőt néhány esetben alkalmazzáka súlyponttól való távolság, az objektum mind transzlációés a súlypont körül forog.A forgatás részletei a távolságtól függnekalkalmazott erő a súlypontig.A repülő tárgyak mozgását ez a harmadik típusú mozgás írja le; a fordítás és a forgatás kombinációja.

az F erő az avektor mennyisége, ami azt jelenti, hogy mind a nagyság, mind airánya hozzá van rendelve. Az erő iránya azért fontos, mert a tárgy mozgása ugyanabba az irányba mutat, mint az erő.Az erő terméke és a gravitáció középpontjától való merőleges távolság egy nem körülhatárolt tárgy esetében,vagy egy zárt tárgy forgócsapjánál a nyomaték vagy a pillanat^Mcalled.A nyomaték vektormennyiség is, és forgást eredményez, ugyanúgy, ahogy egy erő fordítást eredményez. Nevezetesen, egy tárgy, amely állandó szögsebességgel forog, továbbra is folytatódikamíg külső nyomatéknak van kitéve. A nyomaték változást hoz létrea szögsebességben, amelyet szöggyorsulásnak neveznek.

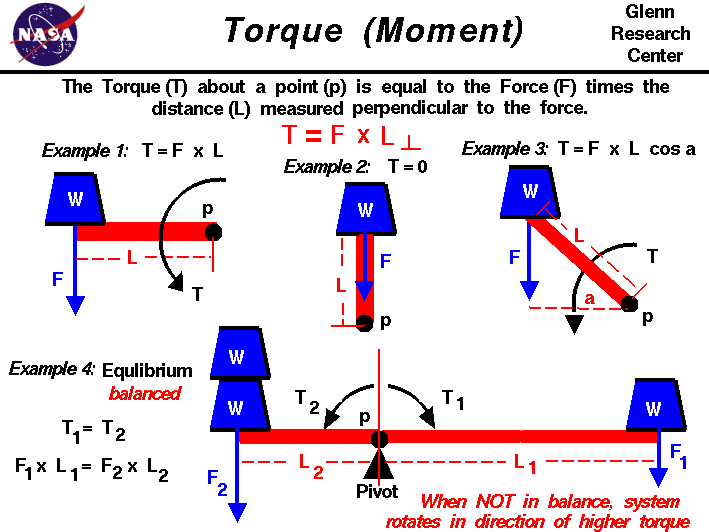
A t nyomaték meghatározásához használt l távolság a P erőtől az erőig terjedő távolság, de az erő irányára merőlegesen mérve.Az ábrán négy példát mutatunk be a nyomatékokra, hogy bemutassuk az irányadó alapelveket torques.In minden példa egy kék súly w hat egy piros sávra, amelyet hívnakegy kar.

az 1. példában az erő (súly) merőlegesena karra. Ebben az esetben a merőleges távolság a tengely hossza, a nyomaték pedig megegyezik a hossz és az erő szorzatával.

a 2.példában ugyanazt az erőt alkalmazzák a karra, de az erő most a pivoton keresztül működik. Ebben az esetben a pivottól az erőre merőleges távolság nulla. Tehát ebben az esetben a nyomaték is nulla.Gondolj egy csuklós ajtóra. Ha megnyomja az ajtó szélét, a csuklópánt felé, az ajtó nem mozogmert a nyomaték nulla.

a 3. példa az az általános eset,amikor az erőt a Kar bizonyos szögében alkalmazzák. A merőleges távolságot adjáktrigonometria, mint a kar hossza (L) A szög szinuszának (cos)szorzata.A nyomaték aztán által adott:

Példa 1 2 levezethető ez az általános képlet,mivel thecosine of0 fok 1.0 (Például 1), majd a koszinusz 90 ° – 0.0 (Például 2).

A 4. példában a pivot a sáv végétől a sáv közepéhez közeli helyre került. A súlyokat mindkét oldalhoz hozzáadjákaz pivot.To a jobb egy súly W termel erő F1 actingat a távolság L1 a pivot. Ez egy T1 nyomatékot hoz létre, amely megegyezik aaz erő és a távolság terméke.

a két súly bal oldalán L2 távolságban F2 erő keletkezik.Ez a T2 nyomatékot a T1-vel ellentétes irányba állítja elő, mert a távolság ellenkező irányba van.

Ha a rendszer egyensúlyban lenne,vagy kiegyensúlyozott lenne, a nyomatékok egyenlőek lennének, és a nettó nyomaték nem hatna a rendszerre.

Ha a rendszer nincs egyensúlyban vagy kiegyensúlyozatlan, akkor a rúd a forgásirányt a nagyobb nyomaték irányába forgatja.Ha F2 = 2 * F1, mi a viszony az L1 és L2 között a rendszer egyensúlyához? Ha F2 = 2 * F1 és L1 = L2, melyik irányba forogna a rendszer?

A légiforgalmi mérnökök az aerodinamikai felület által generált nyomatékot használják a repülőgépek stabilizálására és vezérlésére.A repülőgépeken a vezérlőfelületek termelnekaerodinamikai erők.Ezeket az erőket bizonyos távolságra alkalmazzáka légi jármű cg, ezért a repülőgép forogni kezd. Az előadók remek pillanatokat produkálnak, az előadók egy-egy pillanatot produkálnak, és a nézők egy-egy pillanatot produkálnak. Az a képesség, hogy változtassuk meg az összegetaz erő és a pillanat lehetővé teszi a pilóta számára, hogy manőverezzen vagy legyena repülőgépen.A modellrakéták esetében a hajtóműves repülés során nyomatékot adnak a gravitáció középpontjáról.A sárkányokon az aerodinamika és a súly is nyomatékot ad a pontnak.A kantárponttól való távolság és az erőkifejtés nagysága erős hatással van a sárkány teljesítményére.

tevékenységek:
tárlatvezetés

• Erő, Nyomaték, illetve a Mozgás:
• Alapvető Légi jármű Mozgás:
• Repülőgép Roll Mozgás:
• Repülőgép Pályán Mozgás:
• Repülőgép Yaw Mozgás:
• Szárny:
• Spoiler:
• Liftek:
• Stabilators:
• kormánylap:

a model rocket:

navigáció..

kezdő útmutató Kezdőlap