Jason Által McCormick
docens, Polgári & Environmental Engineering, University of Michigan, Ann Arbor, MI, USA

a Pillanatban kapcsolatok készült téglalap alakú, üreges négyzet strukturális szakaszok (HSS) kapott kisebb figyelmet képest HSS-hogy-HSS kapcsolatok alkotják tengelyirányban betöltött tagok (T-, T-, kereszt-, illetve K-kapcsolatok). Az ezekre a kapcsolatokra összpontosító statikus vizsgálatok többsége Vierendeel rácsos rendszereket vett figyelembe. Ezeket a rendszereket gyakran négyzet vagy téglalap alakú felső és alsó akkordok alkotják, amelyek négyzet vagy téglalap alakú függőleges web (ág) tagokkal vannak összekötve (1.ábra). Ennek a konfigurációnak köszönhetően az akkord-web kapcsolat jelentős hajlításon megy keresztül a nyírási és axiális terhelésekkel együtt, és nem tekinthető rögzített kapcsolatnak, mint általában a tipikus rácsos rendszerekben. Eredetileg fogant 1896-ban Arthur Vierendeel, nem volt, amíg HSS fejlesztették ki, hogy a potenciális Vierendeel fürtös kezdett megvalósulni (Korol et al. 1977), de használatuk megköveteli a pillanat átvitelének megértését a HSS-to-HSS t-kapcsolatok között.

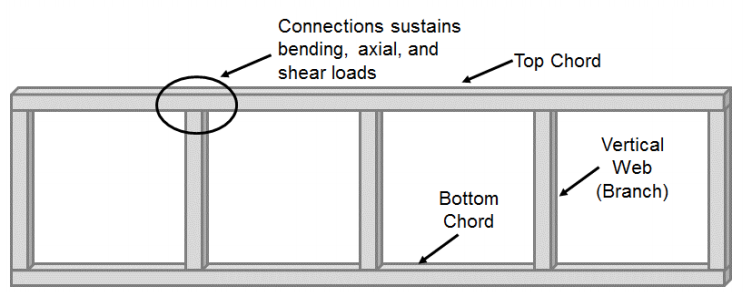
ezeknek a kapcsolatoknak a korai tanulmányai arra összpontosítottak, hogy a kapcsolat képes legyen az ágtag teljes pillanatnyi kapacitásának fejlesztésére. Jubb and Redwood (1966) kimutatta, hogy amikor az ágszakasz szélessége megegyezik az akkordszakaszgal (β=1), a HSS tag teljes pillanatnyi kapacitása megerősítés nélkül érhető el. Ez a tanulmány azonban nem vette figyelembe a pillanatnyi kapacitás potenciális elvesztését az axiális terhelés miatt. Másrészt, Korol et al. (1977) azt mutatta, hogy a kapcsolatok egy kisebb ág szélessége, mint a húrt nem lehet fejleszteni a teljes pillanatban kapacitás a fióktelep nélkül erősítő egy sor 29 különböző kapcsolat vizsgálatokat tekintve, hogy 5 különböző konfigurációk (erősített, ág karima erősítő lemezek, akkord karima stiffeners, haunch, valamint csonka piramis). Általánosságban elmondható, hogy a nem megerősített Vierendeel típusú csatlakozások szilárdsága és merevsége csökken az akkord hajlékonysági arányának (B/t) növekedésével és az ág-akkord szélességi Arány (β) csökkenésével. Ennek eredményeként, unstiffened Vierendeel rácsos típusú kapcsolatok csak akkor tekinthető merev (azaz alávetni minimális relatív elforgatás között az akkordot, fióktelep) ha a fióktelep-hogy-akkord szélesség arány 1.0, valamint az akkord tudjuk arány alacsony, vagy a kapcsolat megerősített (Packer 1993).

mivel ezekben az ízületekben a maximális pillanatok túlságosan nagy deformációkban fordulhatnak elő, hasonló megközelítést alkalmaznak a tengelyirányban betöltött négyzet és téglalap alakú HSS ízületekhez, ahol a végső teherbírás vagy deformáció vagy forgási határ a tervezési pillanat jellemzésére szolgál (Wardenier 1982). Az AISC 360-10 (K3. fejezet) három határállapotot vizsgál a négyzet és téglalap alakú HSS t-csatlakozások esetében statikus síkbeli hajlítás mellett: akkordfal plasztifikáció, oldalfal helyi hajlítás, valamint az ág helyi eloszlása az egyenetlen terheléseloszlás miatt. Az akkordfal plasztifikációja annak a következménye, hogy az ágtag szélessége kisebb, mint az akkord szélessége (β ≤ 0,85), amely megköveteli a hajlítási pillanat által termelt feszültséget és tömörítési terhelést, hogy az akkord viszonylag rugalmas felületén keresztül továbbítsák, nem pedig közvetlenül a merevebb oldalfalakhoz. A határ állami egyenlet (AISC 360-10 Egyenlet K3-6) származtatható hozam vonal elmélete (2. Ábra):

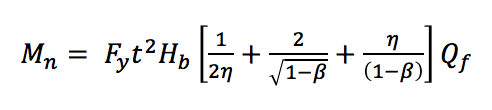
Mn a névleges pillanatban kapacitása a kapcsolat, Fy a megadott minimális folyáshatár a húrt, Hb a teljes magasság a fióktelep, h a csomagtér hossza paraméter megegyezik a magassága a fióktelep osztva a szélessége az akkord (feltételezve, hogy egy 90o szögben között az akkord vagy gyülekezeti tag, mint tipikus Vierendeel fürtös)pedig Qf egy paraméter, hogy csökkentse a kapacitás a közös jelenlétében axiális tömörítés az akkord.

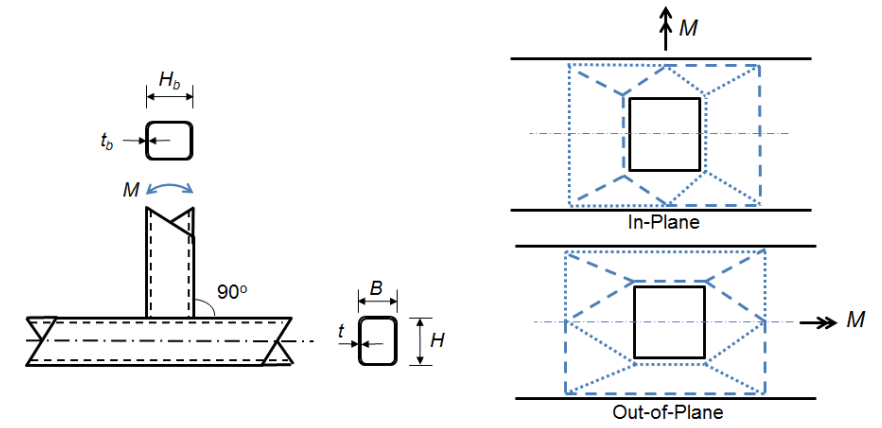
a másik két határállapotok vannak társítva kapcsolatok, ahol a szélessége az ág tag egyenlő vagy majdnem egyenlő a szélessége az akkord (β > 0.85) ami azt jelenti, hogy az ágtag karimáiban kialakult feszültség-és tömörítési terhelések szinte közvetlenül az akkord merevebb oldalfalaiba kerülnek. A határállapot oldalfal helyi hozamú (AISC 360-10 egyenlet K3-7) egy T-kapcsolat ezután levezethető a web helyi hozamú egyenlet koncentrált erők alkalmazott a parttól a végén a tag nagyobb, mint a mélysége (AISC 360-10 egyenlet J10-2):

Mn = 0.5Fyt(Hb + 5t)2
Egyenlet 2

A helyi hozamú az ág miatt egyenetlen terhelés elosztására (AISC 360-10 Egyenlet K3-8) a T-kapcsolat, hatékony szélesség megközelítést alkalmaznak, hogy csökkentsék a kapacitás a megtámasztás tag megszerezni a névleges pillanatban által alkalmazott, a zárójel:

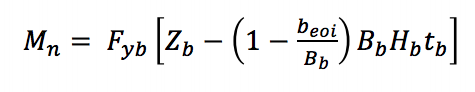
Fyb az ág meghatározott minimális hozamerőssége, Zb az ág műanyag szelvény modulusa a hajlítási tengely körül, a beoi az ág tényleges szélessége, Bb az ág teljes szélessége, a tb pedig az ág tervezési falvastagsága.

mivel korlátozott kísérleti bizonyíték áll rendelkezésre a vierendeel rácsos csatlakozások (t-csatlakozások) speciális tervezési modelljeinek támogatására a síkon kívüli hajlítás alatt, hasonló határértékállapotokat használnak, mint a síkon belüli hajlításhoz (Packer et al. 2010). Egy további határállapot akkord torziós hiba alakul ki a nyomaték alkalmazott az akkord az ág tagja eredményeként a síkon kívüli pillanatban. Ez a nyomaték az akkord rombusz torzulásához vezethet. A síkon kívüli hajlítás névleges momentumegyenletei megtalálhatók az AISC 360-10 K3-9, K3-10, K3-11 és K3-12 egyenletekben. A T-kapcsolatok síkon belüli és síkon kívüli hajlításának egyenletei hasonlóak a nemzetközileg elfogadott egyenletekhez (Packer et al. 2010).

a fenti tervezési egyenleteket a vierendeel rácsos rendszerek statikus terhelések alapján származtatták. Egy friss tanulmány (Fadden et al. 2015) továbbfejlesztette ezt a munkát, hogy figyelembe vegye a négyzet-és téglalap alakú HSS-HSS pillanatnyi csatlakozások viselkedését nagy ciklikus terhelések alatt a csőalapú szeizmikus pillanatkeretrendszerekben (közbenső és speciális pillanatkeretek) való használatra. Egy ilyen rendszer úgy néz ki, hogy kihasználják a kiváló axiális, hajlító, torziós tulajdonságok, nagy szilárdság-tömeg arány, és építészetileg kellemes jellegét négyzet-és téglalap HSS. A nagy torziós ellenállás A gerenda oldalirányú merevítésének csökkenéséhez vezethet, míg a nagy szilárdság / súly arány alacsonyabb szeizmikus tömeget eredményez. Az ilyen csatlakozásoknak azonban képesnek kell lenniük arra, hogy a fénysugár-tag stabil műanyag rögzítésén menjenek keresztül, ahol a fénysugár-tag műanyag kapacitásának 80% – át 0,2 rad-ra tartják. (IMF) vagy 0,4 rad. (SMF) inter-story drift (AISC 341-10). Tekintettel arra, hogy a pillanatnyi keretrendszerek jelenlegi szeizmikus kialakítása megköveteli, hogy a rugalmatlan viselkedés nagy része a gerenda tagban történjen, a gerendatagnak el kell érnie a teljes műanyag kapacitását a helyi csatolás előtt. Fadden, valamint McCormick (2014a) úgy vélte, mind a kísérleti, mind végeselem modellek, hogy meghatározza, korlátozza szélesség-vastagság, valamint mélység-vastagság követelmények HSS alatt hajlítás, mivel azok meghatározott, a jelenlegi AISC Szeizmikus Rendelkezések (AISC 341-10) nagyrészt kifejlesztett tesztek alapján a ciklikus tengelyirányban betöltött HSS tagjai.

meghatározásához megfelelő konfiguráció részletező követelményeket teljesítik ezt az erő, hajlékonyság kereslet, négy különböző hálózati konfigurációk volt kísérletileg vizsgált: két közvetlenül hegesztett erősített kapcsolatok (páratlan meghatározva), valamint két megerősített kapcsolatok (a lemez, mind a külső membrán lemez). Az összes kapcsolat egy HSS 10X10X5/8 oszlopot használt. A közvetlenül hegesztett csatlakozások az AWS D1.1 (2010) által meghatározott előminősítésű CJP hegesztéseket használták. A páratlan csatlakozáshoz a gerenda HSS 12X8X3/8 (β = 0.8) arra utal, hogy az oszlop arcának plasztifikációja aggodalomra adhat okot. Az illesztett csatlakozáshoz a gerenda egy HSS 12X10X3/8 (β = 1.0) volt, amely lehetővé tette a terhelések közvetlen átvitelét az oldalfalba. A szeizmikus pillanatnyi kapcsolatok előminősítésére szolgáló AISC rakodási protokollt (AISC 341-10) használtuk a kapcsolatok betöltéséhez. A kapcsolatok viselkedése a várakozásoknak megfelelően történt, amikor a páratlan kapcsolat deformációt mutatott az oszlop arcán, míg az illesztett kapcsolat képes volt a terhelést az oszlop oldalfalaira átvinni. Mindkét csatlakozás azonban nem sikerült a hegesztés sarkának lábujjában lévő oszlop alapfémének törése miatt (3.ábra). Ez a törékeny hiba 0,4 rad forgatásnál. és 0,5 rad. ennek megfelelően megerősítették, hogy a közvetlenül hegesztett csatlakozások nem biztosítják a megfelelő viselkedést a szeizmikus alkalmazásokhoz.

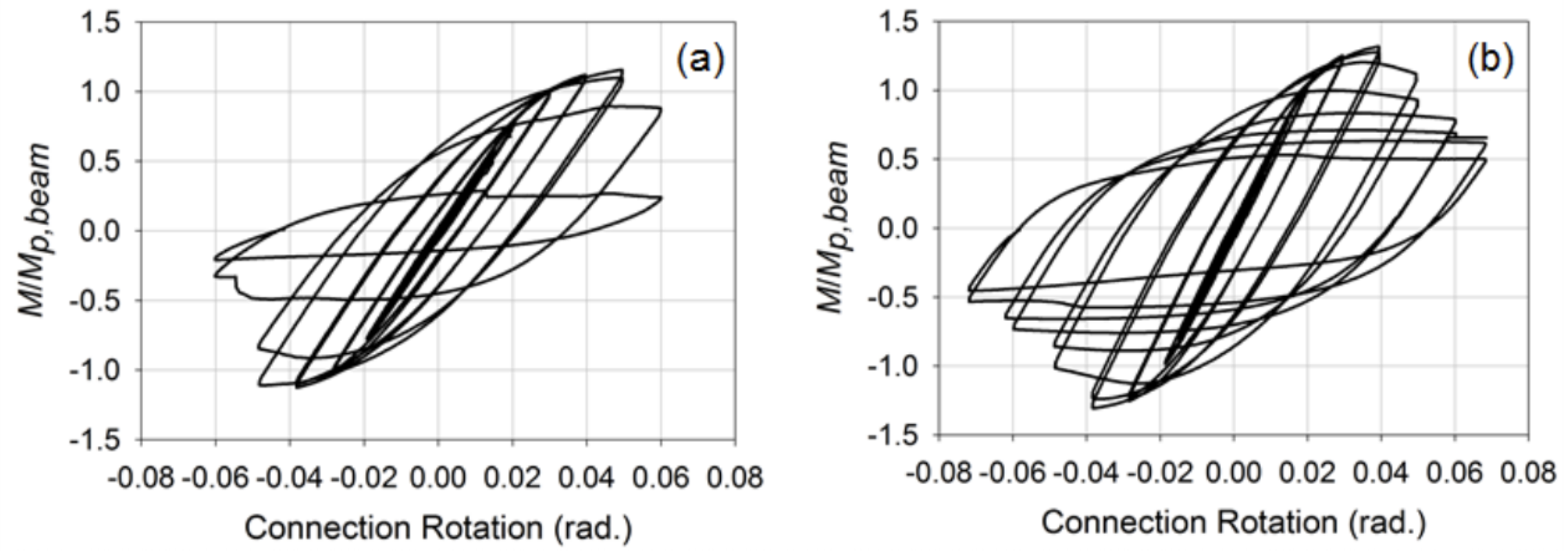
A megerősített kapcsolatok voltak, akkor fejlett figyelembe véve keresztül lemez, mind a külső membrán lemezek, amelyeket gyakran használnak a széles karima gerenda-HSS oszlop kapcsolatokat annak érdekében, hogy egy jobb mechanizmus át a feszültség, tömörítés erők az oldalfalon az oszlop, valamint minimálisra csökkenti a stressz-koncentráció helyezni a varratok. Ezekhez a csatlakozásokhoz a gerendák HSS 12X8X3 / 8 (β = 0,8) tagok voltak. A kapcsolatok tervezéséhez és részletezéséhez használt konkrét eljárásra vonatkozó információk megtalálhatók a Fadden and McCormick (2014B) és a Fadden et al. (2015). Alá vont ugyanaz a terhelés, mint a vasalatlan kapcsolatok a kapcsolatok mutatott egy stabilabb viselkedés a műanyag zsanér előforduló távol az oszlop arcát végén keresztül, vagy külső membrán lemez (4.Ábra). Mindkét kapcsolat képes volt elérni a 0.4 rad értéket is. a forgatás előtt átesett helyi csat, ami degradáció a pillanat kapacitását. A HSS gerenda sarkán azonban törés lépett fel, mivel a nagy forgási szintek 0,7 rad-esek voltak. A kiegyenlített és külső membránlemez-csatlakozások normalizált pillanat-forgási görbéinek összehasonlítása az 5. ábrán látható. Összességében a megerősített csatlakozások ígéretet tettek a HSS-to-HSS szeizmikus pillanatkeret-rendszerek használatára, de több munkára van szükség ahhoz, hogy ezeket a kapcsolatokat az esetleges előminősítés felé mozdítsák.

AISC. (2010). “Seismic Provisions for Structural Steel Buildings”. ANSI/AISC 341-10. American Institute of Steel Construction, Chicago, IL.

AISC. (2010). “Specifications for Structural Steel Buildings”. ANSI/AISC 360-10. American Institute of Steel Construction, Chicago, IL.

AWS. (2010). “Szerkezeti Hegesztési Kód”. ANSI / AWS D1. 1, American Welding Society, Miami, FL.

Fadden, F. és McCormick, J. (2014a). “Finite Element Model of the Cyclic Bending Behavior of Hollow Structural Sections”. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. and McCormick, J. (2014B). “HSS-to-HSS Seismic Moment Connection Performance and Design”. Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D., and McCormick, J. (2015). “Cyclic Testing of Welded HSS-to-HSS Moment Connections for Seismic Applications”. ASCE Journal of Structural Engineering, 141(2), 04014109-1-14.

Jubb, J. E. M. és Redwood, R. G. (1966). “Design ízületek doboz szakaszok”. Az intézmény a strukturális mérnökök, konferencia iparosodott épület és a szerkezeti mérnök, Institute of Structural Engineers, London.

Korol, R. M., El-Zanaty, M., and Brady, F. J. (1977). “Equal Width Connections of Square Hollow Sections in Vierendeel Trusses”. Canadian Journal of Civil Engineering, 4, 190-201.

Packer, J. A. (1993). “Moment Connections between négyszögletes Hollow Sections”. Journal of Constructional Steel Research, 25, 63-81.

Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G. J. és Kurobane, Y. (2010). 3. tervezési útmutató: téglalap alakú üreges szakaszhoz (RHS) illesztések túlnyomórészt statikus terhelés alatt 2.kiadás. CIDECT, Kanada.

Wardenier, J. (1982). “Üreges Szakasz Ízületek”. Delft University Press, Delft, Hollandia.

2016. szeptember

PDF letöltése