a grafikon egy lineáris egyenlőtlenség egy változó egy számsor. < és > nyitott kör használata ≤ és ≥zárt kör esetén.

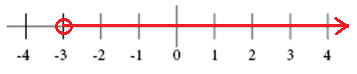
the graph for x > -3

the graph for x ≥ 2

ugyanezt a megoldást egyenértékűnek nevezik. Az egyenlőtlenségek tulajdonságai, valamint az egyenlőség tulajdonságai is vannak. Az összes alábbi tulajdonság igaz a ≥ és ≤egyenlőtlenségekre is.

az egyenlőtlenség Hozzáadási tulajdonsága azt mondja, hogy az egyenlőtlenség mindkét oldalához ugyanazt a számot adja hozzá

$Ha \: x>y,\: akkor\: x+z>y+z$

$If\: x< y,\: ezután\: x + z< y+z$

az egyenlőtlenség kivonási tulajdonsága azt mondja nekünk, hogy ugyanazon szám kivonása az egyenlőtlenség mindkét oldaláról egyenértékű egyenlőtlenséget eredményez.

$$Ha \: x>y,\: akkor\: x-z>y-z$$

$$Ha\: x<y,\: akkor\: x-z<y-z$$

A szorzás ingatlan az egyenlőtlenség azt mondja, hogy szorzás mindkét oldalán egy egyenlőtlenség egy pozitív szám termel egy azonos egyenlőtlenség.

$If\: x > y \: és\: z>0,\: akkor\: xz>yz$$

$$Ha\: x<y\: s\: z>0,\: akkor\: xz<yz$$

Szorzás mindkét oldalon az egyenlőtlen negatív szám, másrészt nem termel egyenértékű egyenlőtlenség, kivéve, ha azt is fordított irányát az egyenlőtlenség szimbólum

$$Ha \: x>y \: s\: z<0,\: akkor\: xz<yz$$

$$Ha\: x<y\: s\: z<0,\: then\: xz>yz$

ugyanez vonatkozik az egyenlőtlenség megosztási tulajdonságára.

a pozitív számmal rendelkező egyenlőtlenség mindkét oldalának felosztása egyenértékű egyenlőtlenséget eredményez.

$$Ha \: x>y \: s\: z>0,\: akkor\: \frac{x}{z}>\frac{y}{z}$$

$$Ha\: x<y\: s\: z>0,\: akkor\: \ frac{x} {z} <\FRAC{y}{z}$

és a negatív számmal rendelkező egyenlőtlenség mindkét oldalán történő felosztás egyenértékű egyenlőtlenséget eredményez, ha az egyenlőtlenség szimbólum megfordul.

$$Ha \: x>y \: s\: z<0,\: akkor\: \frac{x}{z}<\frac{y}{z}$$

$$Ha\: x<y\: s\: z<0,\: akkor\: \frac{x}{z}>\frac{y}{z}$$

megoldani egy többlépcsős egyenlőtlenség teszel, mint amikor megoldása többlépcsős egyenletek. Vegyünk egy dolgot abban az időben, lehetőleg azzal, hogy elkülönítjük a változót az állandóktól. A többlépcsős egyenlőtlenségek megoldásakor fontos, hogy ne felejtsük el megfordítani az egyenlőtlenségi jelet, amikor megszorozzuk vagy elosztjuk a negatív számokat.

példa

oldja meg az egyenlőtlenséget

$-2\bal ( x+3 \jobb) <10$