a bemutató ismerteti a regressziós analízis alapjait, valamint néhány különböző módszert mutat a lineáris regresszió elvégzésére Excelben.

képzelje el ezt: rengeteg különböző adatot kap, és arra kérik Önt, hogy jósolja meg a vállalat jövő évi értékesítési számát. Több tucat, talán akár több száz olyan tényezőt fedezett fel, amelyek esetleg befolyásolhatják a számokat. De honnan tudod, hogy melyek igazán fontosak? Futtassa a regressziós elemzést Excel-ben. Ez ad választ erre és még sok más kérdésre: Mely tényezők számítanak és melyek figyelmen kívül hagyhatók? Mennyire szorosan kapcsolódnak egymáshoz ezek a tényezők? És mennyire lehet biztos a jóslatokban?

• regressziós analízis Excelben
• lineáris regresszió Excelben analízis ToolPak
• rajzoljon lineáris regressziós grafikont
• regressziós analízist Excelben

regressziós analízis Excelben – az alapok

statisztikai modellezésben a regressziós elemzést két vagy több változó közötti kapcsolatok becslésére használják:

függő változó (más néven kritérium változó) a fő tényező, amit megpróbál megérteni és megjósolni.

független változók (más néven magyarázó változók vagy prediktorok) azok a tényezők, amelyek befolyásolhatják a függő változót.

a regressziós analízis segít megérteni, hogy a függő változó hogyan változik, amikor az egyik független változó változik, és lehetővé teszi matematikailag meghatározni, hogy melyik változónak van hatása.

technikailag egy regressziós analízis modell a négyzetek összegén alapul, ami matematikai módszer az adatpontok diszperziójának megtalálására. A modell célja, hogy a lehető legkisebb négyzetösszeget kapja meg, majd rajzoljon egy vonalat, amely a legközelebb áll az adatokhoz.

a statisztikában egy egyszerű és egy többszörös lineáris regressziót különböztetnek meg. Az egyszerű lineáris regresszió egy függő változó és egy független változó kapcsolatát modellezi egy lineáris függvény segítségével. Ha két vagy több magyarázó változót használ a függő változó előrejelzéséhez, akkor több lineáris regresszióval foglalkozik. Ha a függő változó nemlineáris függvényként van modellezve, mivel az adatkapcsolatok nem követnek egyenes vonalat,használjon nemlineáris regressziót. Ennek a bemutatónak a középpontjában egy egyszerű lineáris regresszió lesz.

példaként vegyük az elmúlt 24 hónap árbevételi számait, és derítsük ki az átlagos havi csapadékmennyiséget ugyanebben az időszakban. Telek ezt az információt egy táblázat a regressziós egyenes bizonyítani fogja, hogy a kapcsolat a független változó (csapadék), valamint a függő változó (esernyő értékesítés):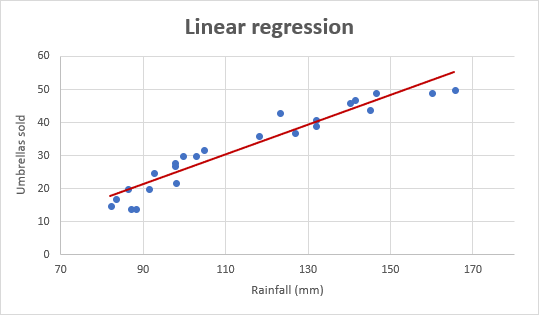

Lineáris regressziós egyenlet

Matematikailag egy lineáris regressziós határozza meg ezt az egyenletet:

, Ahol:

• x független változó.
• y egy függő változó.
• A Az Y-intercept, amely az y várható középértéke, ha minden x változó egyenlő 0-val. Egy regressziós grafikonon ez az a pont, ahol a vonal keresztezi az Y tengelyt.
• b egy regressziós vonal lejtése,amely az y változási sebessége x változásként.
• ε a véletlen hiba kifejezés, amely egy függő változó tényleges értéke és annak előre jelzett értéke közötti különbség.

a lineáris regressziós egyenletnek mindig van egy hibafogalma, mert a való életben a prediktorok soha nem teljesen pontosak. Egyes programok, köztük az Excel, a színfalak mögött elvégzik a hibakeresési számítást. Szóval, az Excel, akkor lineáris regresszió segítségével a legkisebb négyzetek módszerét keresi együtthatók b olyan, hogy:

a példa, a lineáris regressziós egyenlet vesz, a következő formában:

Umbrellas sold = b * rainfall + a

létezik egy maroknyi más módja, hogy megtalálják, valamint b. A három fő módszer, hogy végezze el a lineáris regressziós elemzés az Excel vagy:

• regressziós eszköz tartalmazza Analysis ToolPak
• Scatter chart egy trendline
• lineáris regressziós formula

alább megtalálja a részletes utasításokat az egyes módszerek.

hogyan kell elvégezni a lineáris regressziót az Excelben az Analysis ToolPak

Ez a példa bemutatja, hogyan kell futtatni a regressziót az Excelben egy speciális eszköz használatával, amely az Analysis ToolPak bővítményhez tartozik.

engedélyezze az Analysis ToolPak bővítményt

Analysis ToolPak elérhető az Excel 2019-2003 összes verziójában, de alapértelmezés szerint nincs engedélyezve. Tehát manuálisan kell bekapcsolnia. Így:

1. az Excelben kattintson a fájlra > opciók.
2. az Excel beállítások párbeszédpanelen válassza ki a Bővítmények lehetőséget a bal oldali sávon, ellenőrizze, hogy az Excel bővítmények ki vannak-e jelölve a kezelés mezőben, majd kattintson a Go gombra.
   
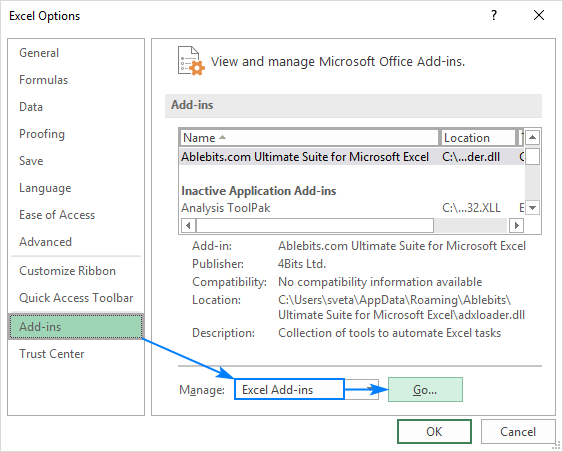
3. a bővítmények párbeszédpanelen jelölje ki az Analysis Toolpak elemet, majd kattintson az OK gombra:
   

Ez hozzáadja az adatelemző eszközöket az Excel szalag adatlapjához.

Run regressziós analízis

ebben a példában egy egyszerű lineáris regressziót fogunk végrehajtani az Excelben. A B oszlopban az elmúlt 24 hónap átlagos havi csapadékmennyiségének listája található, amely független változónk (prediktor), valamint a C oszlopban értékesített Esernyők száma, amely a függő változó. Természetesen sok más tényező is befolyásolhatja az értékesítést, de most csak erre a két változóra összpontosítunk: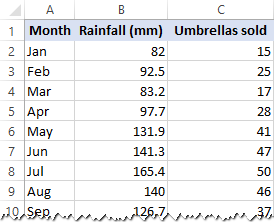

az elemzési Eszközpak engedélyezve van, végezze el ezeket a lépéseket a regressziós elemzés elvégzéséhez Excelben:

1. az adat lapon, az elemzési csoportban kattintson az adatelemzés gombra.
   
2. válassza ki a regressziót, majd kattintson az OK gombra.
   
3. a regressziós párbeszédpanelen konfigurálja a következő beállításokat:
   • válassza ki a bemeneti Y tartományt, amely a függő változó. A mi esetünkben ez esernyő értékesítés (C1:C25).
   • válassza ki az Input X tartományt, azaz a független változót. Ebben a példában ez az átlagos havi Csapadék (B1: B25).

   ha többszörös regressziós modellt épít, válasszon két vagy több szomszédos oszlopot különböző független változókkal.

   • jelölje be a címkék jelölőnégyzetet, ha az X és Y tartományok tetején fejlécek vannak.
   • válassza ki a kívánt kimeneti opciót, esetünkben egy új munkalapot.
   • opcionálisan jelölje be a maradványok jelölőnégyzetet, hogy megkapja a különbséget az előre jelzett és a tényleges értékek között.
     
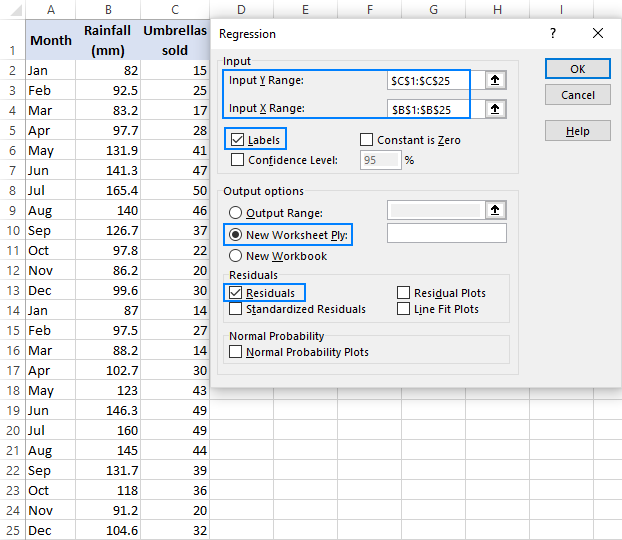
4. kattintson az Ok gombra, és figyelje meg az Excel által létrehozott regressziós elemzési kimenetet.

értelmezze a regressziós analízis kimenetét

ahogy most láttuk, a regresszió futtatása Excel-ben egyszerű, mert minden számítás automatikusan előformálódik. Az eredmények értelmezése kissé trükkösebb, mert tudnia kell, mi van az egyes számok mögött. Az alábbiakban megtalálja a regressziós analízis kimenet 4 fő részének lebontását.

regressziós analízis kimenet: összefoglaló kimenet

Ez a rész megmutatja, hogy a kiszámított lineáris regressziós egyenlet mennyire illeszkedik a forrásadatokhoz.

itt van, amit minden információ jelent:

Több R. Ez a korrelációs együttható méri a két változó közötti lineáris kapcsolat erősségét. A korrelációs együttható bármilyen érték lehet -1 és 1 között, abszolút értéke pedig a kapcsolat erősségét jelzi. Minél nagyobb az abszolút érték, annál erősebb a kapcsolat:

• 1 erős pozitív kapcsolatot jelent
• -1 erős negatív kapcsolatot jelent
• 0 egyáltalán nem jelent kapcsolatot

R négyzet. Ez a meghatározási együttható, amelyet az illeszkedés jóságának jelzőjeként használnak. Megmutatja, hogy hány pont esik a regressziós vonalra. Az R2 értéket a négyzetek teljes összegéből számítják ki, pontosabban az eredeti adatok négyzet alakú eltéréseinek összege az átlagtól.

példánkban az R2 0,91 (2 számjegyre kerekítve), ami tündér jó. Ez azt jelenti, hogy értékeink 91% – a illeszkedik a regressziós elemzési modellhez. Más szóval, a függő változók (y-értékek) 91%-át a független változók (x-értékek) magyarázzák. Általában a 95% – os vagy annál nagyobb R négyzetet jó illeszkedésnek tekintik.

Korrigált R négyzet. Ez az R négyzet a modell független változóinak számához igazítva. Ezt az értéket szeretné használni az R négyzet helyett a többszörös regressziós elemzéshez.

Standard hiba. Ez egy másik jóság-of-fit intézkedés, amely megmutatja a regressziós elemzés pontosságát-minél kisebb a szám, annál biztosabb lehet a regressziós egyenletről. Míg az R2 a modell által magyarázott függő változók varianciájának százalékát jelenti, a Standard hiba abszolút intézkedés, amely azt az átlagos távolságot mutatja, amelyet az adatpontok a regressziós vonaltól esnek.

megfigyelések. Ez egyszerűen a megfigyelések száma a modellben.

Regressziós elemzés kimenet: ANOVA

a második része A kimenet varianciaanalízis (ANOVA):

Tulajdonképpen, ez osztja az összeg négyzetek az egyes komponenseket, amely tájékoztatást ad arról, hogy a szint a változékonyság belül a regressziós modell:

• df száma a szabadságfokot kapcsolódó források a variancia.
• SS a négyzetek összege. Minél kisebb a maradék SS a teljes SS-hez képest, annál jobban illeszkedik a modell az adatokhoz.
• MS az átlagos négyzet.
• F az F statisztika, vagy F-teszt A null hipotézishez. A modell általános jelentőségének tesztelésére szolgál.
• szignifikancia F az F P-értéke.

az ANOVA részt ritkán használják az Excel egyszerű lineáris regressziós elemzéséhez, de feltétlenül alaposan meg kell vizsgálnia az utolsó komponenst. Az F érték jelentősége képet ad arról, hogy mennyire megbízhatóak (statisztikailag szignifikánsak) az eredmények. Ha a szignifikancia F kevesebb, mint 0,05 (5%), a modell rendben van. Ha ez nagyobb, mint 0,05, akkor valószínűleg jobb választani egy másik független változó.

regressziós analízis kimenet: együtthatók

Ez a szakasz konkrét információkat tartalmaz az elemzés összetevőiről:

a szakasz leghasznosabb összetevője az együtthatók. Lehetővé teszi egy lineáris regressziós egyenlet létrehozását Excel-ben:

adatkészletünknél, ahol y az eladott napernyők száma, x pedig egy átlagos havi Csapadék, lineáris regressziós képletünk a következő:

Y = Rainfall Coefficient * x + Intercept

három tizedesjegyre kerekített A és b értékekkel ellátva, három tizedesjegyre kerekítve: Y=0.45*x-19.074

például az átlagos havi csapadékmennyiség egyenlő 82 mm, az esernyő értékesítés mintegy 17.8:

0.45*82-19.074=17.8

hasonló módon, akkor megtudja, hány napernyők lesz értékesített bármilyen egyéb havi csapadék (x változó) adja meg.

regressziós analízis kimenet: residuals

ha összehasonlítjuk a becsült és tényleges száma eladott Esernyők megfelelő havi Csapadék 82 mm, látni fogja, hogy ezek a számok kissé eltérő:

• becsült: 17.8 (fent kiszámítva)
• tényleges: 15 (a forrásadatok 2. sora)

miért van a különbség? Mivel a független változók soha nem tökéletes előrejelzői a függő változóknak. A maradványok segítenek megérteni, hogy a tényleges értékek milyen messze vannak az előre jelzett értékektől:

hogyan készítsünk lineáris regressziós grafikont Excel

Ha gyorsan meg kell jeleníteni a két változó közötti kapcsolatot, rajzoljon egy lineáris regressziós diagramot. Ez nagyon egyszerű! Így:

1. válassza ki a két oszlopot az adataival, beleértve a fejléceket is.
2. a Beágyazott lap, a Beszélgetések csoportban kattintson a Scatter táblázat ikonra, majd válassza ki a Scatter miniatűr (az első):
   

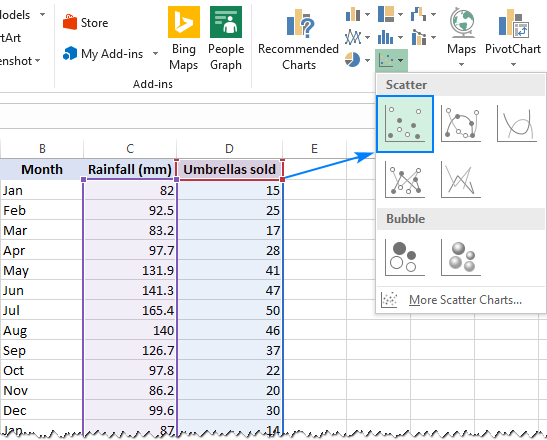
   Ez majd helyezzen be egy scatter plot a munkalap, amely hasonlít ez:
   

3. Most, meg kell rajzolni a legkisebb négyzetek regressziós egyenes. Ehhez kattintson a jobb gombbal bármelyik pontra, majd válassza a Trendline hozzáadása … lehetőséget a helyi menüből.
   
4. A jobb oldali ablaktáblán válassza ki a lineáris trendline alakot, és opcionálisan ellenőrizze a megjelenítési egyenletet a diagramon, hogy megkapja a regressziós képletet:
   

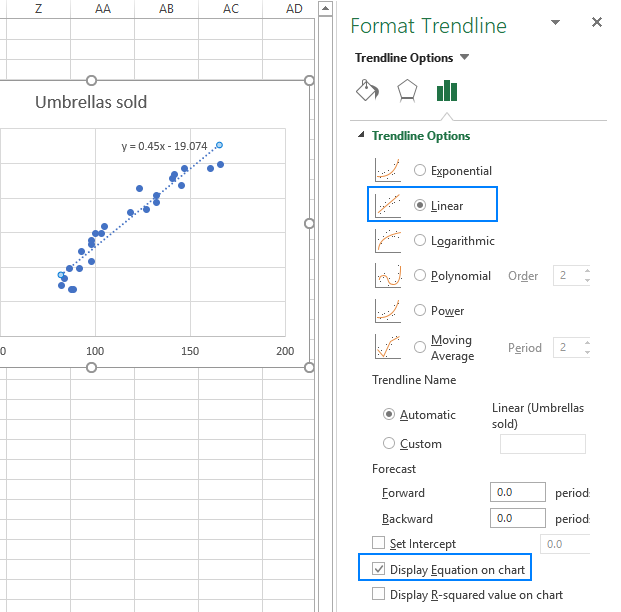
   amint észreveheti, az Excel regressziós egyenlet ugyanaz, mint a lineáris regressziós képlet, amelyet az együtthatók kimenete alapján építettünk.

5. váltás a Fill & sor lapra, majd testreszabhatja a sort tetszés szerint. Például választhat egy másik vonalszínt, és egy szaggatott vonal helyett egy szilárd vonalat használhat (válassza a tömör vonalat a kötőjel típusmezőben):
   

Ezen a ponton a diagram már úgy néz ki, mint egy tisztességes regressziós grafikon:

mégis érdemes néhány további fejlesztést végrehajtani:

• húzza az egyenletet, ahol jónak látja.
• add tengelyek címek (Chart Elements gomb > tengely címek).
• ha az adatpontok a vízszintes és / vagy függőleges tengely közepén kezdődnek, mint ebben a példában, érdemes lehet megszabadulni a túlzott fehér helytől. A következő tipp elmagyarázza, hogyan kell ezt megtenni: méretezze a diagramtengelyeket a fehér tér csökkentése érdekében.így néz ki a javított regressziós gráfunk:
  
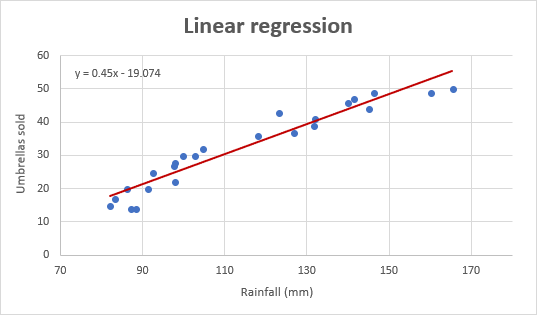  fontos megjegyzés! A regressziós gráfban a független változónak mindig az X tengelyen kell lennie, a függő változónak pedig az Y tengelyen. Ha a grafikon fordított sorrendben van ábrázolva, cserélje ki a munkalap oszlopait, majd húzza újra a diagramot. Ha nem engedélyezi a forrásadatok átrendezését, akkor az X és Y tengelyeket közvetlenül egy diagramban válthatja át.

hogyan kell regressziót végezni az Excelben a

képletekkel a Microsoft Excel néhány statisztikai funkcióval rendelkezik, amelyek segítenek a lineáris regressziós analízis elvégzésében, mint például a LINEST, a SLOPE, az INTERCPET és a CORREL.

a LINEST függvény a legkisebb négyzetek regressziós metódusát használja egy egyenes vonal kiszámításához, amely a legjobban magyarázza a változók közötti kapcsolatot, és visszaadja az adott sort leíró tömböt. Ebben a bemutatóban megtalálhatja a funkció szintaxisának részletes magyarázatát. Most csak készítsünk egy képletet a minta adatkészletünkhöz:

=LINEST(C2:C25, B2:B25)

mivel a LINEST funkció egy értéktömböt ad vissza, tömb képletként kell megadnia. Válasszon két szomszédos cellát ugyanabban a sorban, E2:F2 esetünkben írja be a képletet, majd nyomja meg a Ctrl + Shift + Enter billentyűt a befejezéséhez.

A képlet a b együttható (E1), valamint az állandó (F1) a már ismert lineáris regressziós egyenlet:

y = bx + a

Ha elkerüljük a tömbképletek használata a munkalapok, vagy nem tud számolni, valamint b egyénileg rendszeres képletek:

a Y-tengellyel (a):

=INTERCEPT(C2:C25, B2:B25)

a lejtőn (b): =SLOPE(C2:C25, B2:B25)

Továbbá, megtalálja a korrelációs együttható (R Több a regressziós elemzés összefoglaló kimenet), amely azt jelzi, hogy erősen a két változó kapcsolódnak egymáshoz:

=CORREL(B2:B25,C2:C25)

Az alábbi képen látható ezeket Excel regressziós képletek akcióban:

így végez lineáris regressziót az Excelben. Ennek ellenére kérjük, ne feledje, hogy a Microsoft Excel nem statisztikai program. Ha professzionális szintű regressziós elemzést kell végrehajtania, érdemes célzott szoftvert használni, például XLSTAT, RegressIt stb.

elérhető Letöltések:

ahhoz, hogy közelebbről megnézzük a lineáris regressziós képleteinket és az ebben az oktatóanyagban tárgyalt egyéb technikákat, szívesen letöltjük a minta regressziós elemzését az Excel munkafüzetben.

• hogyan kell használni Solver Excel példákkal
• hogyan kell kiszámítani kamatos kamat Excel
• hogyan kell kiszámítani CAGR (összetett éves növekedési ráta) Excel