a Komplex Számok: Bevezetés (page 1 of 3)

részből áll: Bevezetés, üzemeltetés komplexek, A Másodfokú Formula

eddig azt mondták, hogy nem bírod a négyzetgyök egy negatív szám. Ennek oka az, hogy nem volt olyan számod, amely negatív volt, miután négyzetbe helyezte őket (tehát nem tudott” visszafelé menni ” a négyzetgyök elvételével). Minden szám pozitív volt, miután négyzetbe tette. Tehát nem nagyon lehetett negatívumot mondani, és elvárni, hogy valami értelmes dolgot találjanak ki.

most azonban egy negatív szám négyzetgyökét veheti igénybe,de egy új szám használatával jár. Ezt az új számot feltalálták(felfedezték?) a reformáció idején. Abban az időben senki sem hitte, hogy az új számhoz bármilyen “valós” felhasználás megtalálható, kivéve az egyes egyenletek megoldásában részt vevő számítások megkönnyítését, így az új számot úgy tekintették, mintha a kényelem kedvéért kitalált szám lenne.

(de aztán, ha belegondolunk, nem minden szám találmányok? Ez nem olyan, mint a számok nőnek a fákon! A fejünkben élnek. Mindet kitaláltuk! Miért nem talál fel egy újat, mindaddig, amíg jól működik azzal, ami már van?)

Akkor:

Most, lehet, hogy azt hiszed, hogy:

De ennek semmi értelme! Már van két szám, hogy négyzet 1; nevezetesen -1 és +1. És már a -1-esre céloztam. Tehát nem ésszerű, hogy én is tér 1. Ez rámutat egy fontos részletre: Amikor foglalkozik a fantáziarajz, kapsz valamit (a képesség, hogy foglalkozik a negatívok belső tér gyökerek), de akkor is veszít valamit (néhány rugalmasságot, kényelmes szabályokat, hogy szokott lenni, amikor foglalkozik a tér gyökerei). Különösen először mindig az i-részt kell tennie!

• egyszerűsítse sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Minden jog fenntartva

(figyelmeztetés: a harmadik “egyenlő” jel ” “, nem “”. Az i kívül esik a radikálison.)

• egyszerűsítése sqrt (-25).

• sqrt(-18) egyszerűsítése.

• egyszerűsítse –sqrt(-6).

a számítások, akkor foglalkozik csak, mint x, kivéve azt a tényt, hogy x2 csak x2, de i2 -1:

• Egyszerűsíteni 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• Egyszerűsíteni 16i – 5i.

16I – 5I = (16 – 5)i = 11i

• szorzás és egyszerűsítés (3i)(4i).

(3i)(4i) = (3·4) (i·i) = (12) (i2) = (12)(-1) = -12

• szorzás és egyszerűsítés(i) (2i) (–3i).

(i) (2i) (–3i) = (2 · -3) (i · i · i) = (-6) (i2 · i)

=(-6) (-1 · i) = (-6) (–i) = 6i

Belül látható, hogy , mert i2 = -1. Folytatva, kapunk:

Ez a minta a hatáskörök, jelek, 1 van, hogy egy ciklus:

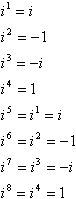
más szóval, A kiszámításához minden magas teljesítmény én, lehet átalakítani, hogy egy alacsonyabb energiát azáltal, hogy a legközelebbi többszörösére 4 ez nem nagyobb, mint a kitevő, majd levonva ez több a kitevő. Például egy közös trükk kérdés tesztek valami mentén “egyszerűsítése i99”, az ötlet, hogy akkor próbálja szorozni I kilencvenkilenc alkalommal, és akkor elfogy az idő, és a tanárok kap egy jó kuncogás az Ön költségén a Kari társalgóban. Így működik a parancsikon:

i99 = i96+3 = i(4×24) + 3 = i3 = –i

azaz i99 = i3, mert akkor csak lop ki az i96. (Kilencvenhat egy többszörös négy, így i96 csak 1, amit figyelmen kívül lehet hagyni.) Más szóval, a kitevőt 4-gyel oszthatjuk (hosszú osztással), eldobhatjuk a választ,és csak a maradékot használhatjuk. Ez megadja a kitevő azon részét, amely érdekli. Íme néhány további példa:

• egyszerűsítse az i17-et.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• I120.

i120 = i4 · 30 = i4· 30 + 0 = i0 = 1

• I64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>