Articles

könnyű permutációk és kombinációk

by admin

mindig összekevertem a ” permutációt “és a” kombinációt ” — melyik melyik?

itt egy egyszerű módja annak, hogy emlékezzen: permutáció hangzik bonyolult, nem igaz? És az is. A permutációkkal minden apró részlet számít. Alice, Bob és Charlie különbözik Charlie, Bob és Alice (helyezze be a barátok nevét ide).

kombinációk, másrészt, elég könnyű megy. A részletek nem számítanak. Alice, Bob és Charlie ugyanaz, mint Charlie, Bob és Alice.

a permutációk listákra vonatkoznak (rendelési ügyek), a kombinációk pedig csoportokra (a rend nem számít).

tudod, a” kombinált zárat “valóban”permutációs zárnak” kell nevezni. Az a sorrend, amit a számokra raksz.

egyszerű permutációk és kombinációk

egy igazi” kombinációs zár ” mind a 10-17-23, mind a 23-17-10 helyes.

permutációk: a szőrös részletek

kezdjük permutációkkal, vagy minden lehetséges módon csinál valamit. Mi a divatos nadrág kifejezés “permutáció”, így fogunk törődni minden utolsó részlet, beleértve a sorrendben az egyes tételek. Tegyük fel, hogy 8 emberünk van:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

hány módon tudunk odaítélni egy 1., 2. és 3. helyezett díjat nyolc versenyző között? (Arany / Ezüst / Bronz)

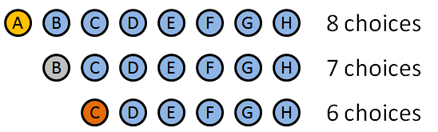
permuation példa érmek

a rend óta permutációkat fogunk használni. Itt van, hogyan bomlik le:

  • Aranyérem: 8 választás: a B C D E F G H (okos, hogyan készítettem a neveket egyeznek meg betűkkel, eh?). Tegyük fel, hogy a nyeri az aranyat.
  • ezüstérem: 7.
  • bronzérem: 6.

bizonyos embereket választottunk, hogy nyerjenek, de a részletek nem számítanak: először 8 választásunk volt, majd 7, majd 6. A lehetőségek száma összesen$8 * 7 * 6 = 336$.

nézzük meg a részleteket. 8-ból 3 embert kellett megrendelnünk. Ehhez elkezdtük az összes lehetőséget (8), majd egyenként elvettük őket (7, majd 6), amíg elfogyott az érmek.

tudjuk, hogy a faktoriális:

\ displaystyle{ 8! = 8 \ cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \ cdot 1}

sajnos ez túl sok! Csak $ – t akarunk 8 * 7 * 6$. Hogyan állíthatjuk meg a faktoriálist 5-kor?

Ez az, ahol a permutációk hűvösek: figyeljük meg, hogyan akarunk megszabadulni$5 * 4 * 3 * 2 * 1$. Mi a másik neve ennek? 5 faktoriális!

tehát, ha 8-at csinálunk!/5! megkapjuk:

\displaystyle{\frac{8!}{5!} = \ frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \ cdot 3 \ cdot 2 \cdot 1} = 8 \cdot 7 \ cdot 6}

és miért használtuk az 5-ös számot? Mert maradt, miután kiválasztottunk 3 érmet a 8-ból. Tehát egy jobb módja annak, hogy ezt írjuk:

\displaystyle{\frac{8!}{(8-3)!}}

ahol 8!/(8-3)! csak egy divatos módja annak, hogy azt mondja: “használja az első 3 szám 8!”. Ha összesen n elemünk van, és egy bizonyos sorrendben k-t akarunk választani, akkor a következő parancsot kapjuk:

\displaystyle{\frac{n!{(n-k)!}}

és ez a képzelet permutációs képlet: n elemeid vannak, és meg akarod találni a K tételek megrendelésének módját:

\ displaystyle{p (n, k) = \frac{n!{(n-k)!}}

kombinációk, Ho!

kombinációk könnyen megy. A rend nem számít. Keverheted, és ugyanúgy néz ki. Tegyük fel, hogy olcsó vagyok, és nem engedhetek meg magamnak külön arany -, ezüst-és bronzérmet. Valójában csak üres konzervdobozokat engedhetek meg magamnak.

hány módon adhatok 3 konzervdobozt 8 embernek?

Nos, ebben az esetben az emberek kiválasztásának sorrendje nem számít. Ha adok egy doboz Alice, Bob, majd Charlie, ez ugyanaz, mint ad Charlie, Alice, majd Bob. Akárhogy is, egyformán csalódottak.

Ez érdekes pontot vet fel — itt van néhány elbocsátás. Alice Bob Charlie = Charlie Bob Alice . Egy pillanatra, csak kitaláljuk, hogy hány módon tudjuk átrendezni 3 emberek.

nos, 3 választásunk van az első személy számára, 2 a második, csak 1 az utolsó számára. Tehát van $3 * 2 * 1$ módon újra rendezni 3 emberek.

várj egy percet … ez egy kicsit olyan, mint egy permutáció! Átvertél!

valóban megtettem. Ha van N ember, és szeretné tudni, hogy hány megállapodások vannak az összes őket, ez csak N faktorial vagy N!

tehát, ha 3 konzervdobozunk van, amit el kell adni, akkor 3 van! vagy 6 variáció minden választáshoz. Ha ki akarjuk deríteni, hány kombinációnk van, akkor minden permutációt létrehozunk, és elosztjuk az összes redundanciával. A mi esetünkben 336 permutációt kapunk (felülről), és minden permutációra 6 redundanciával osztunk, és 336/6 = 56-ot kapunk.

az általános képlet:

\ displaystyle{c (n, k) = \ frac{p(n,k)} {k!}}

ami azt jelenti: “Találd meg az összes módot, hogy k embereket válasszunk n-ből, és osszuk meg a k-vel! változatok”. Ha ezt leírjuk, megkapjuk a kombinált képletet, vagy a k elemek kombinálásának számos módját az n halmazból:

\ displaystyle{c (n, k) = \frac{n!{(n-k)!k!}}

néha C(n,k) van írva, mint:

\displaystyle{\binom {n}{k}}

ami a binomiális együttható.

néhány példa

íme néhány példa a permutációkból származó kombinációkra (a rend nem számít).

  • kombináció: 3 fős csapat kiválasztása egy 10 fős csoportból. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    permutáció: elnök, alelnök és vízipipa kiválasztása egy 10 fős csoportból. $P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • kombináció: 3 desszert kiválasztása 10-es menüből. C (10,3) = 120.

    permutáció: felsorolja a 3 kedvenc desszertjét, sorrendben, egy 10-es menüből. P (10,3) = 720.

ne jegyezd meg a képleteket, értsd meg, miért működnek. A kombinációk egyszerűbbek, mint a permutációk, és azok. Kevesebb kombináció van, mint a permutációk.

A sorozat más hozzászólásai

  1. egyszerű permutációk és kombinációk
  2. navigáljon egy rácson kombinációk és permutációk segítségével
  3. Hogyan értsük meg a kombinációkat szorzással
  4. miért szorozzuk meg a kombinációkat?