Határozott integrálok
először érdemes elolvasni az integráció bevezetését!
integráció
|
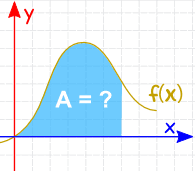
integráció használható területek, kötetek, központi pontok és sok hasznos dolog megtalálására. De gyakran használják arra, hogy megtalálják a területet egy ilyen funkció grafikonja alatt: |
 |
|
|
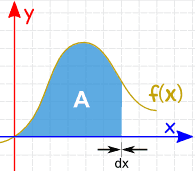
a terület megtalálható a nulla szélességű szeletek hozzáadásával: és vannak olyan integrációs szabályok, amelyek segítenek nekünk a válasz megszerzésében. |
 |
Jelölés
A szimbólum, a “Szerves” elegáns “S” (“Összeg”, az ötlet összefoglalva szelet):
Miután a Szerves Szimbólum tesszük a funkciót akarjuk találni a szerves része (az úgynevezett Integrand).
majd fejezze be a DX-szel, hogy a szeletek x irányba menjenek (és szélességben közelítsék meg a nullát).
Definite Integral
egy határozott integrálnak van kezdő és vég értéke: más szóval van egy intervallum .
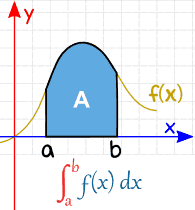
a és b (úgynevezett határok, határok vagy határok) kerülnek az “S” alján és tetején, mint ez:
 |
 |
|
| Definite Integral (from a to b) |
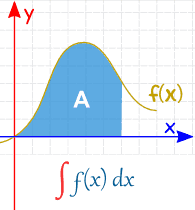
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
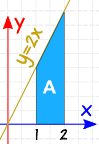
példa: mi az 2 ∫ 1 2x dx
meg kell találnunk A Határozatlan integrált, 1-től 2-ig, 2x DX
először meg kell találnunk A Határozatlan integral.
Az integrációs szabályok alapján megállapítjuk, hogy ∫2x dx = x2 + C
most kiszámoljuk, hogy 1, és 2:
- x=1: ∫2x dx = 12 + C
- x=2: ∫2x dx = 22 + C
kivonjuk:
és a “C” törlésre kerül … szóval a Határozott Integrálok, hogy figyelmen kívül hagyhatjuk C.
az Eredmény:

Ellenőrzése: ilyen egyszerű formában, nézzük is próbálja kiszámítása a terület geometria:
A = 2+42 × 1 = 3
Igen, van egy olyan terület 3.
(Hurrá!)
jelölés: Meg tudjuk mutatni a határozatlan integrál (anélkül, hogy a +C) belül szögletes zárójelben, határértékek, illetve a b után, így:
Példa (folytatás)
Egy jó módja annak, hogy mutassa meg a választ:
=
próbáljuk meg egy másik példa:
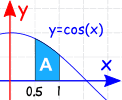
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
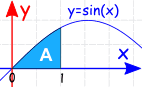
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
A Határozatlan Integrál van: ∫sin(x) dx = −cos(x) + C
Mivel fogunk 0-tól, lehet csak számítani a szerves, az x=1?
−cos(1) = -0.540…
mi? Negatív? De pozitívnak tűnik a grafikonon.
nos … hibát követtünk el!
mert ki kell vonnunk az integráltot x=0 értéken. Nem szabad feltételeznünk, hogy nulla.
tehát csináljuk megfelelően, kivonva az egyiket a másikból:
=
ez jobb!
de negatív régiók is lehetnek, ha a görbe a tengely alatt van:

példa:
A Határozott Integrál, 1-től 3, cos(x) dx:
Észre, hogy valami pozitív, illetve negatív.
a határozott integrál kidolgozza a nettó értéket.
végezzük el a számításokat:
=
ugrás több negatív, mint pozitív a nettó eredmény -0.700….
így van ez a fontos dolog, hogy emlékezzen:
Próbáld integráló cos(x), a másik vége értékeket lásd meg magad, milyen pozitív, illetve negatív munka.
pozitív terület
de néha azt akarjuk, hogy az összes területet pozitívnak kezeljük (anélkül, hogy a tengely alatti részt kivonnánk).
ebben az esetben külön kell kiszámítanunk a területeket, mint például ebben a példában:

példa: Mekkora a teljes terület y = cos (x) és x tengely között, x = 1-től x = 3-ig?
Ez olyan, mint a példa, amit most tettünk, de most arra számítunk, hogy minden terület pozitív (képzeld el, hogy meg kellett festenünk).
- a terület felett a x-tengely
- a terület alatt az x-tengely
A görbe metszi az x-tengely az x = π/2, ezért:
1-Től π/2:
= sin(π/2) − sin(1)
A π/2 3:
= sin(3) − sin(π/2)
Ez utóbbi negatív, de azt akarjuk, hogy pozitív legyen, tehát:
teljes terület = 0.159… + 0.859… = 1.018…
Ez nagyon különbözik az előző példa válaszától.
folyamatos
ó igen, az általunk integrált függvénynek folyamatosnak kell lennie az a és b között: nincsenek lyukak, ugrások vagy függőleges aszimptoták (ahol a függvény felfelé/lefelé halad a végtelenség felé).
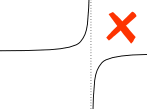
példa:
az A és b közötti függőleges aszimptot a határozott integrálra hat.
tulajdonságok
terület feletti terület
az integrál hozzáadja a tengely feletti területet, de kivonja az alábbi területet, egy “nettó érték” esetén:
az F + G integrálja megegyezik az F plusz integráljával a G integrálja:
Hátrameneti az intervallum
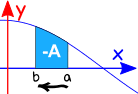
Hátrameneti az irányt a intervallumot ad a negatív az eredeti irányba.
![]()

Leave a Reply