Fibonacci szekvencia
a Fibonacci szekvencia a számok sorozata:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
a következő szám az előtte lévő két szám összeadásával található meg:
- a 2 az előtte lévő két szám (1+1),
- a 3 az előtte lévő két szám (1+2),
- az 5 jelentése (2+3),
- stb.
példa: a következő szám a fenti sorrendben 21+34 = 55
Ez ilyen egyszerű!
itt van egy hosszabb lista:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
meg tudja találni a következő néhány számot?
spirált készít
amikor négyzeteket készítünk ezekkel a szélességekkel, szép spirált kapunk:
látod, hogy a négyzetek szépen illeszkednek egymáshoz?
például 5 és 8 gyártmányú 13, 8 és 13 gyártmányú 21, és így tovább.

Ez a spirál a természetben található!
lásd: A természet, az Aranyarány és a Fibonacci
A szabály
a Fibonacci-szekvencia “szabályként” írható (lásd szekvenciák és sorozatok).
először a kifejezések 0-tól kezdve vannak számozva:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
tehát a 6-os szám X6 (ami 8-nak felel meg).
|
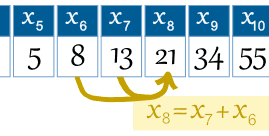
példa: a 8. kifejezés x8 = x7 + x6 |
 |
így írhatjuk a szabályt:
a szabály xn = XN−1 + XN−2
ahol:
- xn kifejezést száma “n”
- xn−1 az előző kifejezés (n−1)
- xn−2 a kifejezés előtt az (n−2)
Példa: távú 9 számítják ki, mint ez:
aranymetszés
ez Pedig egy meglepetés. Amikor két egymást követő (egymás után) Fibonacci számot veszünk, arányuk nagyon közel van a “φ” arany arányhoz, amely körülbelül 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
nem kell 2-vel és 3-mal kezdenünk, itt véletlenszerűen 192-t és 16-ot választottam (és megvan a sorrend 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
hosszabb időt vesz igénybe a jó értékek elérése, de azt mutatja, hogy nem csak a Fibonacci-sorozat képes erre!
az Aranyarányt használva a Fibonacci-számok kiszámításához
és még ennél is meglepőbb, hogy bármilyen Fibonacci-számot kiszámolhatunk az Aranyarány segítségével:
xn = φn − (1−φ)n√5
a válasz egész számként jelenik meg, pontosan megegyezik az előző két kifejezés hozzáadásával.
példa: x6
x6 = (1.618034…)6 − (1−1.618034…)6√5
amikor számológépet használtam erre (csak az Aranyarányt 6 tizedesjegyre adtam), megkaptam a választ 8.00000033, pontosabb számítás közelebb lenne a 8-hoz.
próbálja meg n=12 és nézze meg, mit kap.
Azt is számítani egy Fibonacci Számot megszorozzuk az előző Fibonacci-Szám, amelyet az aranymetszés aztán kerekítés (működik a számok felett 1):
Példa: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (lekerekített)
néhány érdekes dolog
itt van a Fibonacci sorozat újra:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
van egy érdekes minta:
- nézd meg az x3 = 2 számot. Minden 3. szám a következők többszöröse 2 (2, 8, 34, 144, 610, …)
- nézd meg az x4 = 3 számot. Minden 4. szám egy többszörös 3 (3, 21, 144, …)
- nézd meg az x5 = 5 számot. Minden 5. szám egy többszöröse 5 (5, 55, 610, …)
stb. (Minden n-edik szám xn többszöröse).
1/89 = 0,011235955056179775…
figyeljük meg az első néhány számjegy (0,1,1,2,3,5) a Fibonacci szekvencia?
oly módon, hogy mindegyik, kivéve több számjegyű számok (13, 21, stb) átfedés, mint ez:
… stb …
0.011235955056179775… = 1/89
feltételek nulla alatt
a szekvencia nulla alatt is működik, mint ez:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(bizonyítsa be magának, hogy minden számot úgy talál, hogy előtte összeadja a két számot!)
valójában a nulla alatti szekvenciának ugyanazok a számai vannak, mint a nulla feletti szekvenciának, kivéve, ha a + – + – – – t követik … minta. Így írható:
x−n = (-1) n+1 xn
, amely azt mondja, hogy a “−n ” kifejezés egyenlő (-1) n+1-szeres “n” kifejezéssel, és az érték (-1)n + 1 szépen teszi a helyes +1, -1, +1, -1, … minta.
történelem
Fibonacci nem volt az első, aki tudott a sorozatról, Indiában több száz évvel ezelőtt ismert volt!

Fibonacciról a férfi
valódi neve Leonardo Pisano Bogollo volt, és 1170 és 1250 között élt Olaszországban.
“Fibonacci” volt a beceneve, ami nagyjából azt jelenti, hogy “Bonacci fia”.
amellett, hogy híres a Fibonacci Szekvenciáról, segített a Hindu-arab számok terjesztésében (mint a jelenlegi számok 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) Európán keresztül a római számok helyett (I, II, III, IV, V stb.). Ez megmentett minket egy csomó bajt! Köszönöm Leonardo.

Fibonacci nap
Fibonacci nap November 23., mivel az” 1, 1, 2, 3 ” számjegy a sorozat részét képezi. Tehát következő November 23 tudassa mindenkivel!


Leave a Reply