a 4 színű probléma az egyik leghíresebb matematikai probléma. Több mint száz évig ellenállt a bizonyítéknak, mielőtt végül elbukott; végül volt egy érvényes bizonyíték, de az egyik, amely több mint ezer órányi számítógépes időre támaszkodott. Jim Tilley kutatása azt sugallja, hogy végül drámai egyszerűsítés lehetséges. Felfedezte azt a tulajdonságot, Kempe-reteszelést, hogy a 4 színű tétel minimális ellenpéldájának ki kell mutatnia, és széles körű vizsgálatok alapján megfogalmazta azt a feltételezést, hogy a Birkhoff gyémánt az egyetlen alapvető Kempe-reteszelő konfiguráció.

A grafikon színezése magában foglalja a címkék vagy színek hozzárendelését egy gráfként ismert matematikai objektum csúcsaihoz. A négyszínű probléma az algebrai gráfelmélet fejlődésének egyik eredeti motivációját szolgáltatta. Grafikon színezésére használják számos valós problémák, mint például a konfliktusok minimalizálása, amikor ütemezés sport események, tervezési vizsgálat ütemterve szervezésével ülő tervek, még akkor is, CCTV kamera elhelyezése egy épületben sok a sarok annak érdekében, hogy minimálisra csökkentsék a kamera átfedés. Azt is biztosítja az alapot Sudoku rejtvények.

A 4-colour probléma
Francis Guthrie, a híres brit matematikus és logikus Augustus De Morgan tanítványa 1852-ben jelentette a 4-colour problémát. Megfogalmazta a problémát olyan térképekkel kapcsolatban, amelyek megfelelnek bizonyos feltételeknek, például nem tartalmaznak lyukakat, és minden régiót (például országot vagy államot) összekapcsolnak úgy, hogy két vagy több nem összefüggő részen ne legyen régió. Guthrie azt állította, hogy az ilyen térképek Soha nem fog több, mint Négy színben színezni a térképet, hogy nincs két szomszédos régió azonos színű.

Manapság, a 4-színű probléma kifejezve grafikonok, ahelyett, színező régiók térképek, egy szín csúcsot, grafikonok. A 4 színű tétel minden létező bizonyítéka azt mutatja, hogy egy minimális ellenpélda nem létezhet. (A minimális ellenpélda a legkisebb síkgráf, amely több mint négy színt igényel a csúcsainak megfelelő színezéséhez.) Csak olyan síkgráfokat kell figyelembe venni, amelyek háromszögletűek, mivel minden olyan gráf, amely nem háromszögelés, az élek beillesztésével alakítható át. Ha a kapott háromszögelés 4-colourable, akkor az eredeti gráf is 4-colourable. Nagyon hasznos, ha korlátozhatjuk az ellenőrzést a háromszögelésre.

korai bizonyítási kísérlet
azok közül, akik bizonyítékot kínáltak, Alfred Bray Kempe, egy angol ügyvéd és amatőr matematikus volt az a személy, akinek hírnevét leginkább rontotta sikertelen erőfeszítései. Sikereit 1879-ben jelentette be, “bizonyítéka” az American Journal of Mathematics című folyóiratban jelent meg. Tizenegy évvel később, azonban, egy másik angol matematikus, Percy Heawood, létrehozott egy térképet, amelyet 4 színezett a végső régióig oly módon, hogy Kempe módszere kudarcot vallott az adott végső régióban. Kudarca ellenére Kempe hasznos eszközt hagyott-egy Kempe láncot. Ez egy maximális, összekapcsolt (minden csúcs, amely bármely másból elérhető az élek mentén) algráf, amelyben minden csúcs pontosan két színt használ. A Kempe-láncok bizonyítottan közreműködnek a színező-és újraszínező grafikonok kialakításában. Lásd Az 1. Ábrát.

megdöbbentő egyszerűsítés lenne
Ha a Birkhoff gyémánt önmagában a 4-színezés kulcsa.

Proof at last
Az első érvényes bizonyítást Kenneth Appel és Wolfgang Haken jelentette be 1976-ban. Több mint ezer órányi számítógépes időt igényelt az érvelés bizonyos aspektusainak ellenőrzése. Ez az elképzelés támaszkodva számítógépes kód, potenciálisan tartalmazó emberi indukált hibák (és a kód tette!), ahelyett, hogy “emberi” bizonyíték lenne, nem elégítette ki a matematikai közösség nagy részét. Appel és Haken bizonyítéka elegáns volt a teljes szerkezetében, de a részletek csúnyák voltak.

a bizonyítékot 1996-ban finomította egy négy matematikusból álló csapat: Robertson, Sanders, Seymour és Thomas, de még mindig számítógépes kódra támaszkodtak a bizonyíték kitöltéséhez. 2010-ben Steinberger újabb variációt ajánlott fel. Azonban még mindig nincs teljesen kielégítő válasz arra, hogy miért igaz a 4-színes tétel. (Miután a sejtés bebizonyosodott, megszerezte a ” tétel státuszát.”)

alternatív bizonyíték keresése
A 4-színű probléma olyan könnyen megfogalmazható és megérthető, hogy sok ezer Amatőr matematikus érdeklődését felkeltette, mindannyian azt hiszik, hogy egyszerű klasszikus bizonyítékot találnak, és így híressé válnak. Jim Tilley apja, 1978-1984 között a Kanadai Királyi Katonai Főiskola fizikusa és igazgatója volt. Amikor úgy érezte, hogy áttörést ért el, megkérte fiát, Jimet, hogy ellenőrizze munkáját. Jim mindig talált egy hibát. Mégis, annak ellenére, hogy a kezdeti szkepticizmus, hogy az apja erőfeszítései valaha is gyümölcsöt, ő lett fertőzött lelkesedéssel a 4-színes probléma, és elkezdte tanulmányozni intenzíven.

Kempe-locking
Jim Tilley kutatása egy új tulajdonság felfedezéséhez vezetett, amelyet a 4-szín tétel minimális ellenpéldájának kell mutatnia. Kempe-zárnak nevezte el.”Rájött, hogy valószínűleg összeegyeztethetetlen egy másik tulajdonsággal, amelyet egy minimális ellenpéldának ki kell mutatnia-viz., hogyan kapcsolódik egy grafikon (hány csúcsot kell eltávolítani egy grafikonból, mielőtt szétesik).

Tilley ‘ s Kempe-locking egy háromszög alakú élhez kapcsolódó tulajdonság. A fogalom az X és y szomszédos csúcsok közötti XY él törlésével kezdődik. Ha a kapott gráf minden 4-színezésénél, amelyben az x és y színei azonosak, a Kempe-láncokon nincs olyan színcsere-sorrend, amely miatt az x színe eltér az y színétől, akkor az eredeti háromszögelés állítólag Kempe-reteszelt a XY széléhez képest. Tilley bebizonyította, hogy a 4 színű tétel minimális ellenpéldáját minden egyes széléhez képest be kell zárni; a minimális ellenpélda minden szélének rendelkeznie kell ezzel a színező tulajdonsággal.

A Kempe-reteszelés különösen korlátozó állapot, amelyet nehezebb kielégíteni, mivel a háromszögelés nagyobb lesz. Tilley elhatározta, hogy felfedezi, van-e valami közös a Háromszögeléseknél, amelyek Kempe-zárt élekkel rendelkeznek. A legkorábbi keresés Kempe-zár vezetett rá, hogy a Birkhoff diamond.

a Birkhoff gyémánt
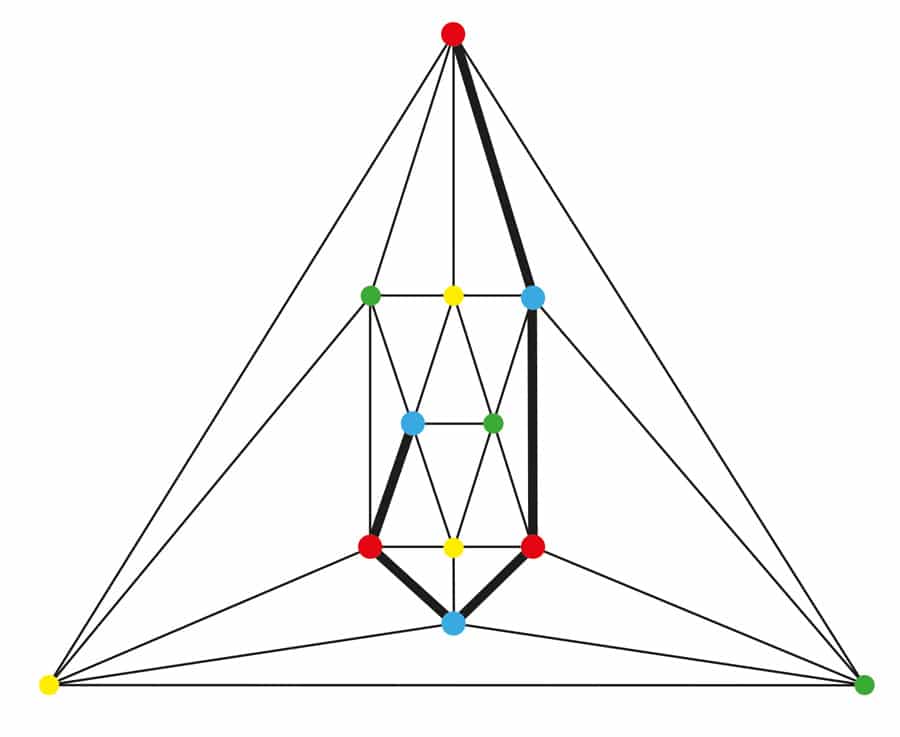
1913-ban G. D. Birkhoff felfedezte, hogy a térképen tíz ország egy bizonyos konfigurációja (hat ország határgyűrűje, amely négy országot tartalmaz) fontos tulajdonsággal rendelkezik. Ha ez a konfiguráció egy térképen van jelen, és ha a konfigurációt eltávolító altérkép 4-colourable, akkor a teljes térkép 4-colourable lesz. Így egy minimális ellenpélda nem tartalmazhatja az adott konfigurációt. Birkhoff gyémánt néven vált ismertté. Tilley úgy találta, hogy egy Kempe-zárolt él xy úgy tűnik, hogy csak akkor merül fel, ha x és y is a végpontjai a grafikon változata Birkhoff gyémánt. Lásd A 2. Ábrát.

a sejtés könnyen megfogalmazható, érthető és érdekes, és meggyőző magyarázatot ad arra, hogy miért minden síkgráf 4-colos.

nem találkozott semmilyen Kempe-reteszelő konfigurációval Birkhoff gyémánt nélkül, azt feltételezte, hogy a Birkhoff gyémánt az egyetlen “alapvető” Kempe-reteszelő konfiguráció, amely nem tartalmaz kisebb Kempe-reteszelő konfigurációt. Tilley azonban úgy találta, hogy nem tudja bizonyítani kritikus sejtését. Frusztráló volt, mert ha igaz, a sejtés közvetlenül bizonyítja a 4-szín tételt. (Ahhoz, hogy minimális ellenpélda legyen, a háromszögelésnek tartalmaznia kell egy Birkhoff gyémánt algráfot, de ha igen, akkor nem lehet minimális ellenpélda.)

elsöprő támogató eset
a sejtés bizonyítása helyett Tilley a következő legjobb dolgot tette. Úgy döntött, hogy kísérletező szerepet játszik, és egy elsöprő ügyet épít a sejtés alátámasztására. Az összes releváns sík háromszöget két osztályra osztotta: azokat, amelyekben legalább négy csúcsot el kell távolítani, mielőtt a Grafikonok szétesnek (4-összekapcsolva), és azokat, amelyekben legalább öt csúcsot el kell távolítani, mielőtt a Grafikonok szétesnek (5-összekapcsolva). Lásd A 3. Ábrát. Tilley kiterjedt kutatásában hasznos volt, hogy minden izomorfizmus osztálynak csak egy tagját kellett megvizsgálnia (szerkezetileg azonos grafikonok). Tilley mind a 8 044 izomorfizmus-osztályt, a 4-kapcsolt planáris triangulációkat legfeljebb 15 csúcson, mind az 5-összekapcsolt planáris triangulációk mind a 9 733 izomorfizmus-osztályát, legfeljebb 24 csúcsponton vizsgálta. Csak három Kempe-zárt háromszöget talált. Mindegyik felfedezett Kempe-zárt él egy Birkhoff gyémántot tartalmazott, mindegyik egy 4-összekapcsolt háromszögben történt. Az 5-összekapcsolt háromszögek között egyáltalán nem volt.

Tilley kiterjesztette keresését a 4-összekapcsolt háromszögek között azáltal, hogy mind a 30,926 izomorfizmusosztályt 16 csúcson, mind a 158,428 izomorfizmusosztályt 17 csúcsponton vizsgálta. A számítás-idő korlátai azt jelentették, hogy a keresést 100 000 véletlenszerűen generált, nem izomorf triangulációra korlátozták 18,19-es és 20 csúcsú osztályokra. A kibővített keresés felbukkant 45 további Kempe-zárolt háromszögelések, de pontosan ugyanazok az eredmények, mint az eredeti keresés: minden Kempe-zárolt él egy háromszögelés szerepelt egy kapcsolódó Birkhoff gyémánt.

Honnan?
Tilley kiterjedt keresései könnyen megerősítették, hogy a Birkhoff diamond alapvető Kempe-reteszelő konfiguráció. Alaposan megvizsgálta a sejtését, de ez nem bizonyított. Ha (vagy amikor) Tilley sejtése igaznak bizonyul, azaz hogy a Birkhoff gyémánt önmagában a 4-színezés kulcsa, akkor a probléma meghökkentő egyszerűsítése lenne: egyetlen konfiguráció, amely mindent megmagyaráz – matematikai elegancia.

A 4 színű sejtés bizonyításához számos kiemelkedő matematikus erőfeszítésére volt szükség. Tilley feltételezése, hogy a Birkhoff gyémánt az egyetlen alapvető Kempe-zár konfiguráció, még nehezebb bizonyítani. A kísérleti bizonyítékok azonban erősek. A teoretikusok azt mondhatják: “Miért zavarja?”Tilley válasza az, hogy a kielégíthetetlen kíváncsiság ki fog derülni:” végül is a sejtés könnyen kijelenthető, érthető és érdekes, és meggyőző magyarázatot kínál arra, hogy miért minden síkgráf 4-colourable.”