értékelése Cohen Kappa

értéke kappa lehet kevesebb, mint 0 (negatív). A pontszám 0 azt jelenti, hogy van véletlen megállapodás között raters, míg a pontszám 1 azt jelenti, hogy van egy teljes megállapodás a raters. Ezért a 0-nál kisebb pontszám azt jelenti, hogy kevesebb egyetértés van, mint véletlenszerű esély. Az alábbiakban megmutatom neked a képletet, hogy ezt kidolgozd, de fontos, hogy megismerd magad a 4. ábrával, hogy erős megértést kapj.

Az oka, hogy kiemelt két rács világossá válik, de most hadd törjem le minden rács.

A = > azon esetek száma, amelyeket mindkét rater helyesnek tartott. Az árusok egyetértenek.

B = > az összes példányok száma, hogy Rater 2 mondta helytelen volt, de Rater 1 mondta helyesek voltak. Ez egy nézeteltérés.

C = > az összes példányok száma, hogy Rater 1 mondta helytelen volt, de Rater 2 mondta helyesek voltak. Ez szintén nézeteltérés.

D = > azon példányok száma, amelyeket mindkét Rater szerint helytelenek voltak. Az árusok egyetértenek.

annak érdekében, hogy dolgozzanak ki a kappa érték, először meg kell tudni, hogy a valószínűsége megállapodás (ez magyarázza, hogy miért emelte ki a megállapodás átlós). Ezt a képletet úgy származtatják, hogy hozzáadják azokat a teszteket, amelyekben a minősítők egyetértenek, majd elosztják azt a tesztek teljes számával. A 4. ábra példáját használva ez azt jelentené (a + D)/(A + B+ C+ D).

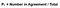
tökéletes! A következő lépés a véletlenszerű megállapodás valószínűségének kidolgozása. Segítségével ábra 4 útmutatóként, a várható érték az összes alkalommal, hogy Dater 1 mondta helyes osztva az összes példányszám, szorozva az összes alkalommal, hogy Dater 2 mondta helyes osztva az összes példányszám, adunk a teljes hányszor, hogy Dater 1 mondta helytelen szorozva a teljes hányszor, hogy Riter 2 mondta helytelen. Ez egy csomó információt, hogy ott, így a 6. ábrán már megfogalmazták ezt az egyenletet a fenti rács.

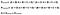
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

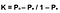
nagyszerű! Most már képes különbséget tenni a megbízhatóság és az érvényesség között, elmagyarázni Cohen kappa-ját és értékelni azt. Ez a statisztika nagyon hasznos, bár mivel megértettem, hogyan működik, most úgy gondolom, hogy az algoritmusok egy adott metrikusra történő optimalizálásakor alulfelhasználható. Ezenkívül Cohen kappa is jó munkát végez mind a többosztályos, mind a kiegyensúlyozatlan osztályproblémák mérésében.

P. S. Ha van valami, amit azt akarja, hogy fedezzem az adatok tudományával kapcsolatban, akkor üzenetet küldhet nekem a Twitteren @KurtisPykes vagy válaszolhat erre a bejegyzésre.