beanz magazin
Merian-Erben (1652) térképe a Wikipédián
az e havi matematikai puzzle 1735-re nyúlik vissza, amikor először Leonhard Euler svájci matematikus és fizikus oldotta meg.
a rejtvényt Königsberg hét hídjának nevezik. Ez alapján a tényleges város, majd Poroszországban, most Kalinyingrád Oroszországban. A várost egy folyó osztja két sziget között, majd, tovább lefelé, a folyó újra felosztja a várost.
a probléma megtévesztően egyszerű: Euler idejében hét híd köti össze a két szigetet és a város downstream részeit. Euler azon töprengett, vajon képes-e valaki egyszer-egyszer átsétálni a hét híd mindegyikén, hogy megérintse a város minden részét. A kezdés és a Befejezés ugyanott nem volt követelmény.
itt van egy térkép, amellyel megpróbálhatja megoldani a problémát:
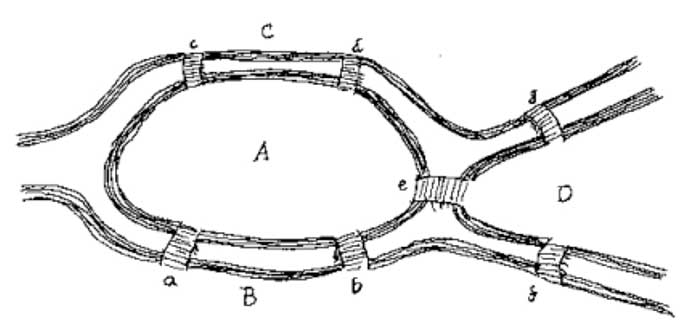
fontos megoldani ezt a problémát: a hidak száma vagy az egyes hidak elhelyezkedése?
válasz: a hidak száma.
Euler bebizonyította, hogy a hidak számának páros számnak kell lennie, például hét helyett hat hídnak, ha egyszer át akar menni minden hídon, és Königsberg minden részébe utazni. A megoldás az egyes hídokat végpontként, a csúcsot matematikai értelemben, valamint az egyes híd (csúcs) közötti kapcsolatokat tekinti. Euler rájött, hogy csak páros számú híd hozta meg a helyes eredményt, mivel képes volt megérinteni a város minden részét anélkül, hogy kétszer átkelne egy hídon.
Euler a matematikával bizonyította, hogy mind a hét hidat csak egyszer lehet átlépni, és Königsberg minden részét felkeresni. Ezzel egy sor felfedezést és betekintést indított el arról, hogyan határozható meg a tér és a metsző terek, valamint azok tulajdonságai. Euler megoldásának részletes leírása a cikk alatti Wikipedia linkben.
ha láttál már mobius csíkot, például láttál egy topológiai példát, egy matematikai tanulmányi terület alakult ki Euler megoldásából erre a problémára. A topológia a térrel és azzal foglalkozik, hogy a dolgok hogyan kapcsolódnak egymáshoz, valamint a tér folytonosságával és határaival. A topológia azt is vizsgálja, hogy a tér tulajdonságai hogyan változnak, és nem változnak, amikor a tér kibővül vagy összehúzódik.
a számítástechnikában a topológia hasznos annak megértésében, hogy a hálózatok (útvonalak) adatok bármely rendszeren belül áramlhatnak, valamint hogy az adatkészletek hogyan kapcsolódhatnak egymáshoz. A hét híd Königsberg is hasonló egy másik gyakori számítási probléma úgynevezett néha az utazó ügynök probléma, ahol megpróbálja megtalálni a leghatékonyabb útvonalat adott egy sor korlátozások, mint a hét hidak Euler probléma.
nem matematikusok (valószínűleg te, határozottan én) tapasztalja meg az utazó ügynök problémáját bármikor, amikor vonattal vagy busszal érkezünk. Az utazó ügynök problémája a meghatározott távolságú városok közötti utazás leghatékonyabb módja. A véges útvonalakon közlekedő szűkös erőforrások (vonatok, buszok) kezelése tökéletes megoldás a számítástechnika számára, mivel a számítógépek gyorsabbak és hatékonyabbak. De először Euler-re és másokra van szükségünk, hogy megállapítsuk a problémát, és matematikai megoldásokat határozzunk meg. Ezután programozzuk a számítógépeinket, hogy elvégezzük a matematikát.
a topológia a halmazelmélettel is foglalkozik, hogyan lehet a dolgok csoportjait halmazokba rendezni, hogy azonosítsák a közös elemeket más csoportokkal, valamint az egyedi elemeket. A Venn diagram egy nagyszerű példa egy készletre. A programozásnak néha különböző módon kell rendeznie az adatokat. Melyik rendezési módszer működik a legjobban egy helyzet lehet meghatározni halmazelmélet.
és mi történt a hét híddal Euler idejéből? Kettő nem élte túl a második világháborút, két hidat lebontottak és egyetlen autópályára cseréltek. A fennmaradó három híd közül az egyiket 1935-ben újjáépítették, míg a másik kettő sértetlen marad, mivel Euler ismerte őket. Természetesen Königsberg, Poroszország megváltoztatta a nevét Kalinyingrádra, Oroszországra.
Leave a Reply