az “Interstellar” film box office sikerével sokan izgatottak a féreglyukak kilátásairól, mint a csillagközi szállítás eszközeiről. Bár jelenleg nincs bizonyíték arra, hogy ilyen egzotikus tárgyak léteznek a természetben, lehetséges, hogy mesterségesen létrehozhatók, talán a magasabb dimenziós húrelmélet és az alapvető tér-idő hab tervezésének változataiból. A féreglyuk-kutatás ma izgalmas téma, évente több tucat, lektorált folyóiratban publikálnak, de érdemes emlékeztetni annak eredetére-és meglepő helyről indul.

1915-ben Albert Einstein kiadta általános relativitáselméletét, a gravitáció leírását, amely szépen meghatározza, hogy az objektumok hogyan vonzzák egymást, és befolyásolják a körülöttük lévő teret és időt. Sok évvel később John Wheeler amerikai fizikus a “space tells matter how to move, and matter tells space how to curve”kifejezést használta. Einstein a gravitációt a tér-idő görbületének megnyilvánulásaként írta le. Az általános relativitáselmélet egy folytonos térelmélet, ellentétben az anyag részecskeelméletével, amely kvantummechanikához vezetett.

Einstein részt vett a kvantummechanika fejlesztésében is, az elmélet, amely a szubatomi részecskéket írja le. De nem volt teljesen elégedett a benne rejlő bizonytalanságokkal és valószínűségi karakterrel. Tehát 1935-ben Nathan Rosennel dolgozott, hogy általános relativitáselméletet készítsen az elektronok számára. Tanulmányuk címe: “a részecske problémája az Általános relativitáselméletben”. Einstein és Rosen egy atomisztikus anyag-és elektromosságelmélet lehetőségét vizsgálták, amely a diszkontinuitások (szingularitások) kivételével az általános relativitáselmélet leírásán (metrikus) és Maxwell elektromágneses elméletén kívül más változót nem használt. Az egyik következmény az volt, hogy a legelemibb töltött részecskét nulla tömegnek találták.

végül, amit előállítottak, valami egészen eredeti volt. Elkezdték az egyenletek egy spherically szimmetrikus tömegeloszlás, már régen a fekete lyukak, valamint ismert, mint a Schwarzschild-megoldás,

$$ds^2 = -\dfrac{1}{1-2m/r}dr^2 – r^2(d\theta^2+\sin^2\theta d\pi^2) + (1-2m/r)dt^2$$

amennyiben \(ds^2\) a metrikus s \(m=GM/c^2\) a gömb alakú koordináták \((r,\theta,\phi)\), valamint időt \(t\).

koordináta-transzformációt hajtottak végre a görbületi szingularitást tartalmazó régió eltávolítására, a tér görbületének megszakítására, amelyet fekete lyukak és hasonló jelenségek jeleztek. A \(r=2M\) szingularitást a \(u^2 = r – 2M\) koordináta – transzformáció eltávolította, ami végső megoldást eredményezett,

$ds^2 = -4(u^2 + 2m)du^2 – (u^2 + 2M)^2 D\Omega^2 + \dfrac{u^2}{u^2 + 2m} dt^2$

ahol \(D\Omega^2 = D\theta^2) + \Sin^2\Theta d\PHI^2\).

Ez a megoldás a fizikai tér matematikai ábrázolása volt két aszimptotikusan lapos lap térével, amelyeket egy híd vagy egy Schwarzschild féreglyuk “torokkal” összekötött. Ez összeköti a két lapot, analógia útján a valódi, háromdimenziós univerzum két különálló részét. Az 1. ábra a féregjárat körüli teret mutatja, a fenti és az alatti tér a “széleken” lapossá válik, miközben a végtelenre közelít.

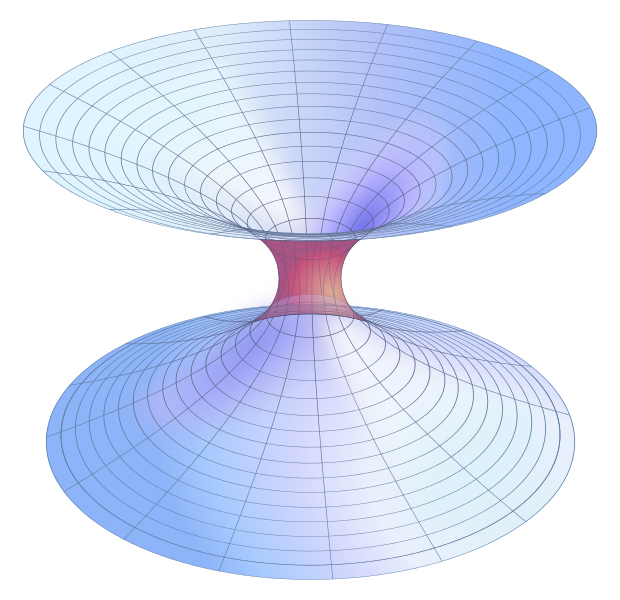
most ez nem volt átjárható féregjárat, ezért John Wheeler fizikusok érkezését kellett várnunk az 1950-es években, Kip Thorne pedig az 1980-as években. 1987-ben, Carl Sagan “Contact” (később játékfilm) című regényének ösztönzésére Thorne és kollégája, Michael Morris egy matematikai leírást, egy metrikát tudott összeállítani egy gömbszimmetrikus és statikus féreglyuk leírására, valós, véges, kerületű. Ennek koordinált csökkenése volt a negatív végtelenségtől — a minimálisan ívelt térben-a minimális értékig, ahol a torok található, majd a toroktól a pozitív végtelenségig növekszik — egy másik minimálisan ívelt térben. Ez a megoldás megkülönböztető jellemzője, hogy nincs eseményhorizont-ellentétben a fekete lyukkal. A Thorne and Morris című lap “féreglyukak a tér-időben és azok használata a csillagközi utazáshoz: az általános relativitáselmélet tanításának eszköze”címmel jelent meg. Ez a tanulmány segített létrehozni féreglyuk kutatás, mint új terület a tudományos kutatás.

azóta számos tanulmány jelent meg, sőt csillagászati felméréseket is végeztek, a legtávolabbi csillagokat és galaxisokat kutatva a természetes féreglyukak után kutatva. Még nem sikerült azonosítani, de ne feledje, hogy ennek a kutatási területnek az eredete-az Einstein-Rosen-híd nem volt átjárható féregjárat, és nem a szerző szándéka volt, hogy készítsen egyet, mégis elkészítették a féregjárat első matematikai leírását. Erre emlékezni kell. A tudományos kutatás gyakran meglehetősen váratlan dolgot hoz létre, amelynek következményei messze meghaladják a kutatók eredeti szándékait.

Kelvin F. Hosszú

a cikk megjelenése óta magazinunk, a Principium két kérdést tett közzé (9.szám & 10), ahol részletesebben tárgyalunk a féreglyukakról és az Einstein-Rosen hídról. Ezek a kérdések részletezik az egynapos szimpóziumot a “csillagközi féreglyukak: fizika és gyakorlati megvalósítás” címmel, amelyet a csillagközi tanulmányok kezdeményezése szervezett a brit bolygóközi társadalommal együttműködve.