a lendület megőrzése a fizikai alapfogalomaz energia és a tömegkonzervációjával együtt.A Momentum meghatározása szerint egy objektum tömege szorozva az objektum sebességévelaz objektum.A lendület megőrzése kimondja, hogy bizonyos problématerületen belül a lendület mennyisége állandó marad;a lendület nem jön létre, nem pusztul el, hanem csak megváltozik a Newton ‘ s laws of motion által leírt erők hatására.A lendülettel foglalkozni nehezebb, mint a tömeggel és az energiával foglalkozni, mert a tömeg és az energia mennyisége egyaránt nagy és nagy. A lendület mind a háromban megmaradfizikai irányok egyszerre. Még nehezebb az agák kezelésébenmert az egyik irányba ható erők befolyásolhatják a lendületet egy másik iránybanA sok molekula ütközése miatt.Ezen a dián egy nagyon, nagyon egyszerűsített áramlási problémát mutatunk beahol a tulajdonságok csak egy irányban változnak.A problémát tovább egyszerűsíteni, figyelembe véve, hogy egy folyamatos áramlás, amely nem változik az idő korlátozásával erőket, hogy csak thoseassociated a thepressure.Légy tudatában annak, hogy igazi flow problémák annál complexthan ez simpleexample.

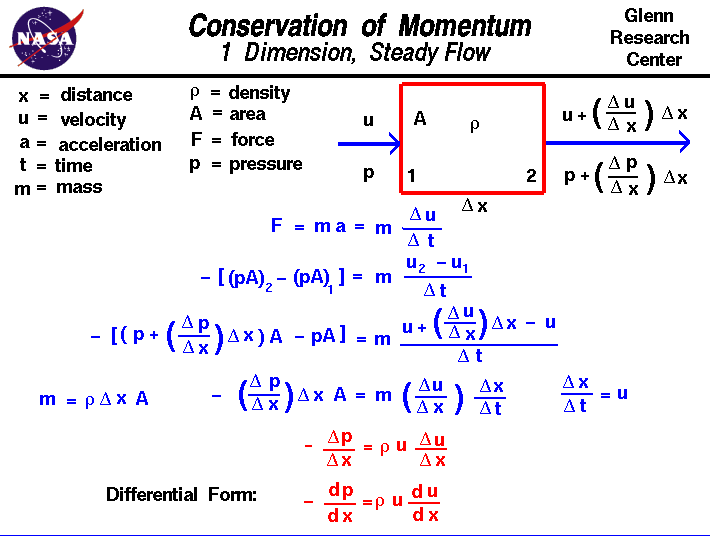
tekintsük a gáz áramlását egy olyan tartományon keresztül, amelyben az áramlási tulajdonságokcsak egy irányba változik, amelyet “x” – nek hívunk. A gáz az 1-es domainat állomásra jut némi u sebességgel, a 2-es állomáson pedig egy kis nyomással, a sebesség és a nyomás eltérő értékével. Az egyszerűség kedvéért feltételezzük, hogyaz r sűrűség állandó marad a domainen belülés hogy az a terület, amelyen keresztül a gáz áramlik, állandó marad. Az 1-es és a 2-es állomások helyét del x-nek nevezett távolsággal választják el egymástól (a Delta a slideand kis háromszöge a görög “d”betű. A matematikusok gyakran használják ezt a szimbólumot a jelölésheza mennyiség változása vagy változása. A webes nyomtatási betűtípus nem támogatjaa görög betűk, ezért csak “del” – nek hívjuk.) A távolságváltozást gradiensnek nevezikhogy elkerüljék a zavart az idővel való változással, amelyet sebességnek neveznek.A sebesség gradienst del u / del X jelzi;a sebesség változása a távolban. Tehát a 2-es állomáson a sebességet a sebesség adja meg1 plusz a gradiens szorozza meg a távolságot.

:

Newton második mozgásállapota F erő megegyezik a lendület időbeli változásával. Egy tárgy állandó massm ez csökkenti a tömeg alkalommal gyorsulás a.An a gyorsulás a sebesség változása az idő változásával (del u / del t). Ezután:

az erő ebben a problémábana nyomásgradiensből származik. Mivel a nyomás egységnyi területre eső erő, a folyadéktartományunkon a nettó erő a nyomás szorosa a területnek aexit mínusz a nyomás szorosa a bejáratnál lévő területnek.

a kifejezés elején a mínusz jelet használják, mivel a gázok nagynyomású régióból alacsony nyomású régióba mozognak; ha a nyomás withx-szel növekszik, a sebesség csökken. A gyorsaságra vonatkozó kifejezéseink helyettesítéseés nyomás:

egyszerűsítés:

Megjegyezni, hogy (del x / del t) thevelocity meg, hogy a tömeg sűrűsége r-szer mennyisége (area alkalommal del x):

Egyszerűsítése:

A del p / del x del u / del xrepresent a nyomás, sebesség-gradiens.Ha pszichiáter a domain le differenciál méretben, ezek a gradiens vált különbsége:

Ez egy dimenziós, állandósult formában ofEuler-Egyenlet.Érdekes megjegyezni, hogy a nyomás dropof egy folyadék (a kifejezést a bal oldalon) arányos mind az értéke thevelocity a gradiens a sebesség.Ennek a lendület egyenletnek a megoldása adja meg a dinamikai nyomás formájátamely abernoulli egyenletében jelenik meg.

tevékenységek:
vezetett túrák

• alapvető folyadékdinamikai egyenletek:

navigáció ..

kezdő útmutató Kezdőlap