A matematika inkább maraton, mint sprint-ez egy hosszú, lassú és egyenletes grind, ritka áttörési pillanatokkal. Mégis, időnként megkapjuk azokat a díjazott “Eureka” pillanatokat, azokat a rövid betű-és számsorokat, amelyek örökre megváltoztatják a tudományt. Íme néhány a leghíresebb egyenletek, az ókori görögök a modern fizika.

Pythagora tétele (IE 530)

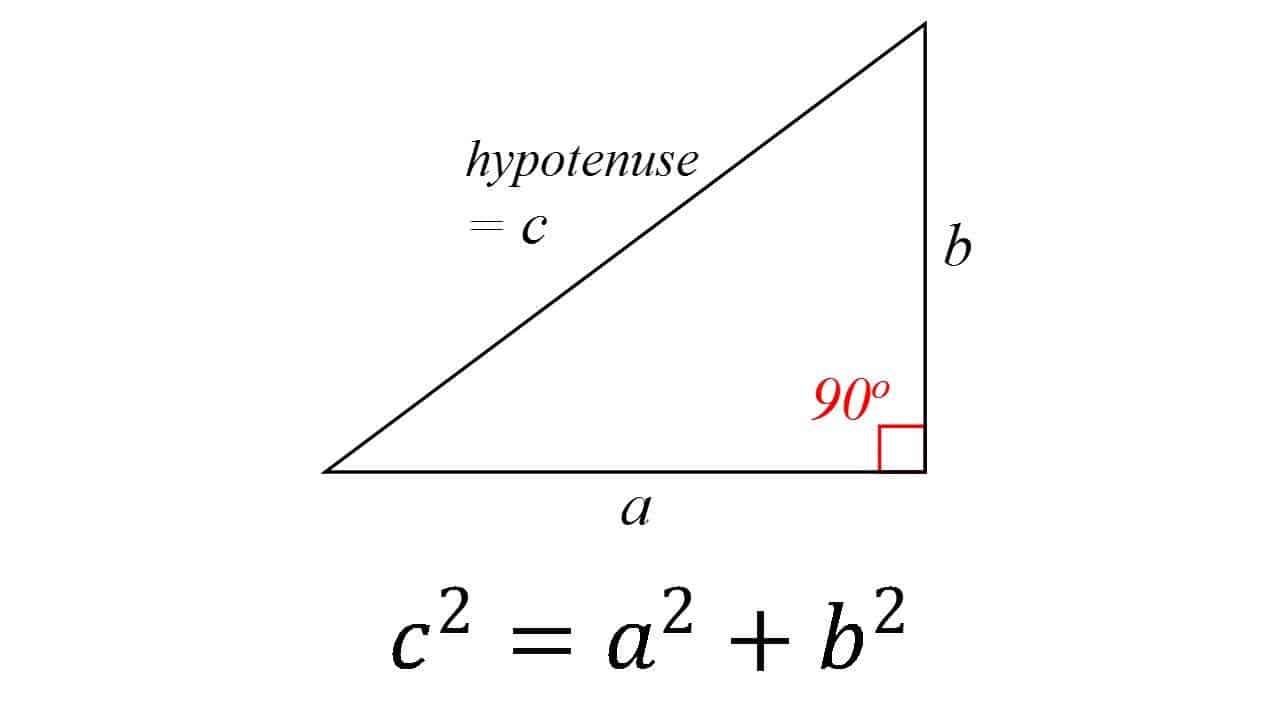
Ez elég az egyik alapító pillér minden geometria: egy jobb háromszögben a hipotenusz négyzete (a derékszögvel ellentétes oldal) megegyezik a másik kettő négyzetének összegével. Az elméletet általában a görög matematikusnak, Pythagorasnak tulajdonítják, bár van némi bizonyíték arra, hogy a babiloni matematikusok megértették a képletet. Az is nagyon lehetséges, hogy a tételt sokan ismerték, de ő volt az első, aki bizonyította.

a tétel számos bizonyítékot kapott-valószínűleg a legtöbb matematikai tétel esetében. Nagyon változatosak, beleértve mind a geometriai bizonyítékokat, mind az algebrai bizonyítékokat, néhányukkal társkereső évezredek óta.

komplex számok

az olasz matematikus, Gerolamo Cardano az első ismert, aki komplex számokat vezetett be, akkoriban “fiktívnek” nevezte őket. Azonban az “i” matematikai fejlődését, mint a -1 négyzetgyökét ábrázoló képzeletbeli számot Leonhard Euler-nek, az emberi történelem egyik legfontosabb matematikusának és tudósának tulajdonítják.

a komplex számok alapvetően olyan számok, amelyek valójában nem léteznek, de amelyek számos számításhoz nagyon hasznosak. Állnak a számok egy igazi része (a számok mind tudjuk), valamint egy képzeletbeli része (az itt képviselt), valamint gyakorlati alkalmazások számos területen, köztük a fizika, a kémia, a biológia, a közgazdaságtan, a villamosmérnöki, illetve a statisztikák.

A logaritmus

a Logaritmus alapvetően az inverz függvény exponentiation. Szüksége van egy szám (N), egy bázis (a), valamint a logaritmusát N a bázis lesz x, ahol az N értéke egy, hogy a hatalom az x-et. Úgy tűnhet, mintha csak egy másik módja az írás ugyanaz a dolog (egy értelemben), de a logaritmus van számtalan gyakorlati alkalmazások használják, a pszichológia, a gazdaság, valamint a mérések számos fizikai jelenségek (pl. pH, vagy földrengés nagysága).

a logaritmusokat John Napier nyilvánosan terjesztette 1614 — ben, a Mirifici Logarithmorum Canonis Descriptio című könyvben (a logaritmusok csodálatos szabályának leírása) – egy illeszkedő cím. A logaritmus különleges esete a természetes logaritmus-e, ahol e egy irracionális és transzcendentális szám, amely megközelítőleg 2.71828182845. Valójában e maga is lenyűgöző történelemmel és lenyűgöző számú alkalmazással rendelkezik, de ez egy másik történet.

Calculus

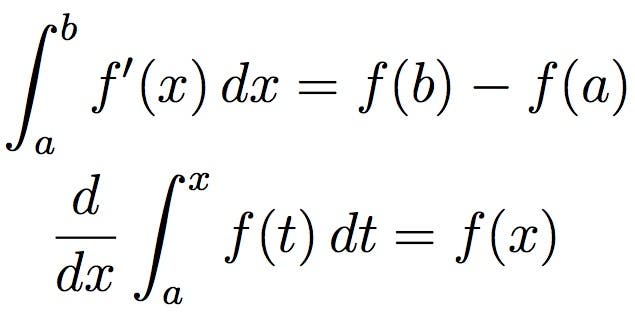
A matematika néhány területe ugyanolyan hatásos volt, mint a kalkulus. A 17. században Isaac Newton és Gottfried Wilhelm Leibniz fejlesztette ki, a kalkulust széles körben használják a tudományban, a mérnöki és a közgazdaságtanban. A kalkulus általában a kis mennyiségek, különösen a végtelenül kis mennyiségek kezelésére összpontosít. A kalkulus segítségével ezek valós számokként kezelhetők, annak ellenére, hogy technikailag végtelenül kicsiek.

egy egyszerűbb vizualizációhoz a fent ábrázolt integrációt úgy lehet elképzelni, mint egy függvény által meghatározott görbe alatti terület mérését.

A gravitáció törvénye

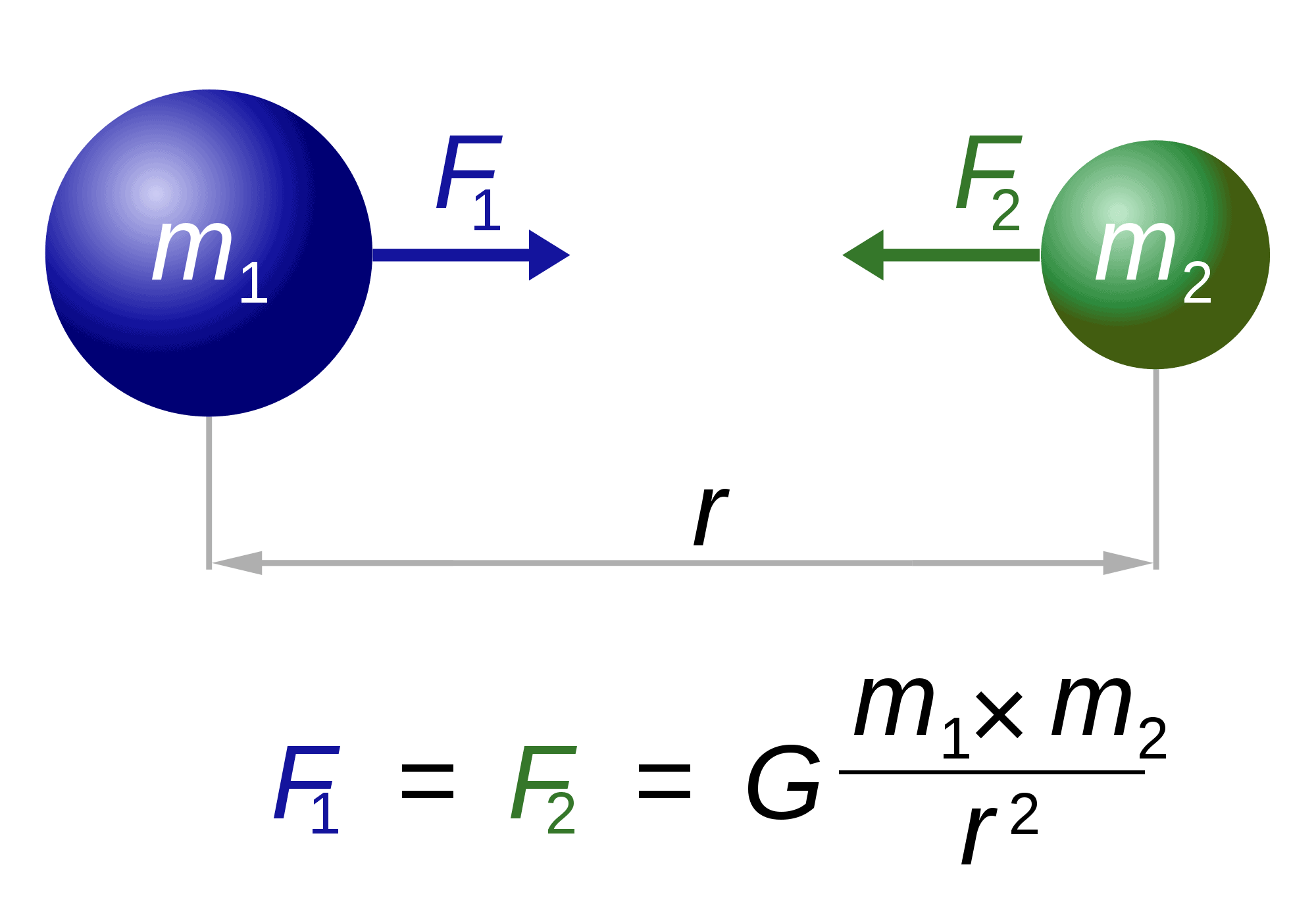
Apropó Newton, ő is “felelős” a világ egyik leghíresebb és leglátványosabb egyenletéért: a gravitáció törvényéért.

a törvény alapvetően azt írja le, hogy az m1 és az m2 tömegű testek hogyan vonzódnak egymáshoz. Az erő (F1, F2) fordítottan arányos a köztük lévő távolság négyzetével (r). Az egyetlen fennmaradó tényező, a G egy gravitációs állandó. Ennek az állandónak a természete továbbra is megfoghatatlan.

általános relativitáselmélet

közel 200 évig Newton törvénye meghatározta a mechanika megértésének szintjét. Einstein munkája a 20. században a következő szintre vitte a dolgokat — ez a két eredmény torony a fizika világának legmagasabb talapzatán.

az általános relativitáselmélet lényegében a gravitáció geometriai elmélete, általánosítva Newton elméletét, amely a gravitáció egységes leírását adja a tér és az idő — vagy a téridő geometriai tulajdonságaként. Különösen Einstein nemcsak azt mutatta, hogy van olyan dolog, mint a” téridő”, amely egyesíti a három dimenziót az idő 4.dimenziójával, hanem azt is megmutatta, hogy ezt a téridőt gravitációval lehet hajlítani, a görbület közvetlenül kapcsolódik bármilyen anyag és sugárzás energiájához és lendületéhez.

A termodinamika második törvénye

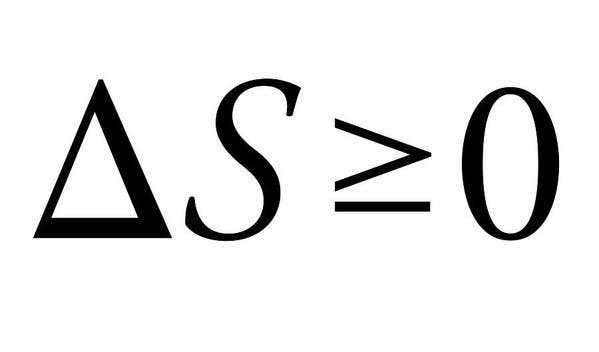
A termodinamika második törvénye az, hogy miért nem lehet szép dolgok az univerzumban. Vicceket félretéve, a termodinamika négy törvénye meghatározza a termodinamikai rendszereket jellemző alapvető fizikai mennyiségeket (hőmérséklet, energia és entrópia). A második különösen az egyszerűsége, de abszolút hatalmas következményei miatt kiemelkedik itt.

a törvény lényegében kimondja, hogy a kölcsönhatásban lévő termodinamikai rendszerek entrópiáinak összege mindig növekszik, vagy legfeljebb állandó marad. Amikor az energia egyik formáról a másikra változik, vagy az anyag mozog, az entrópia (vagy rendellenesség) egy zárt rendszerben nő. A különbség a hőmérséklet, nyomás, sűrűség általában lapos ki egy idő után

Maxwell Egyenletek

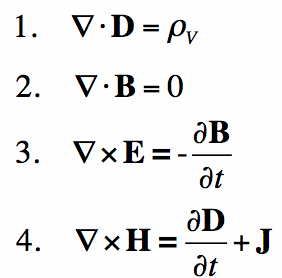
Egyszerűen fogalmazva, a Maxwell-egyenleteket, hogy az elektromágnesesség, amit Newton törvénye, hogy a mechanika. Matematikai alapot nyújtanak a klasszikus elektromágnesességhez, a klasszikus optikához és az elektromos áramkörökhöz. Ezeket széles körben használják abban a készülékben, amelyen ezt olvasod — alapvetően minden elektronikus eszköz.

Maxwell törvényei leírják, hogy az elektromos és mágneses mezőket hogyan generálják a töltések, áramok és a mezők változásai. Jelentős áttörést jelentett az a demonstráció, hogy az elektromos és mágneses mezők fénysebességgel terjednek.

Euler Személyazonosságát

Végül, ez egészen biztos, hogy a legtöbb, elegáns egyenlet, egy dolog, a legfőbb szépség, mert magában foglalja a “basic” számok:

• 0, ami semleges összeadás, illetve kivonás;
• 1, ami semleges szorzás, osztás;
• e, amely az Euler-számot (lásd fent), a bázis a természetes logaritmus;
• i az imaginárius egység (lásd fent); és
• π a Pi, a kör kerületének az átmérőjéhez viszonyított aránya.

egy olyan kapcsolat megtalálása, amely egyesíti ezeket a számokat, nem más, mint lélegzetelállító, és elég valószínűtlennek tűnik. A demonstráció nem éppen egyszerű, de itt is látható.

Ez csak illik, hogy a Stanford Egyetem matematika professzor Keith Devlin leírt egyenlet, mondván, hogy “olyan, mint egy Shakespeare-i szonett, amely rögzíti a lényege a szeretet, vagy egy festményt, ami kiemeli a szépségét, az emberi forma, amely sokkal több, mint csak a bőr mély, Euler egyenlet eléri a nagyon mélyén létezés”

Ez nem gyakran, hogy a matematika-fizika szűkülnek le, hogy egyszerű, elegáns egyenletek—, de ha mégis, elég a látvány.