Bevezetés

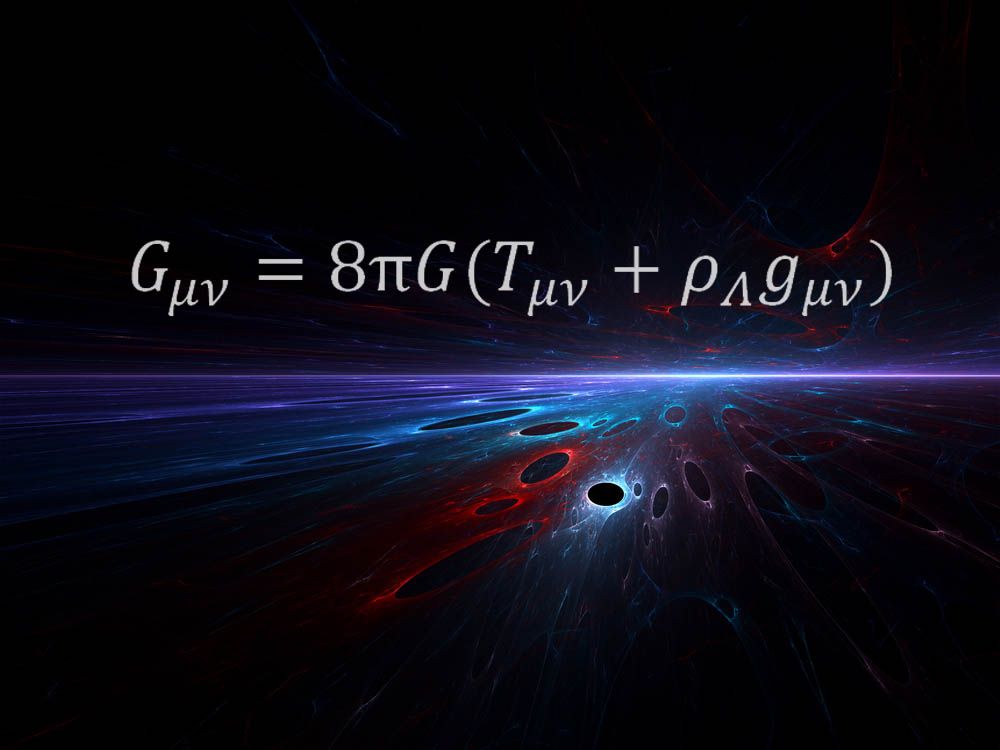
a matematikai egyenletek nem csak hasznosak — sokan nagyon szépek. Sok tudós elismeri, hogy gyakran szeretik a különleges képleteket, nem csak a funkciójukért, hanem a formájukért, valamint az egyszerű, költői igazságokért.

míg bizonyos híres egyenletek, mint például Albert Einstein E = mc^2, a nyilvános dicsőség nagy része, sok kevésbé ismert képletnek vannak bajnokai a tudósok között. LiveScience kérte, fizikusok, csillagászok, matematikusok a kedvenc egyenletek; itt van, amit találtunk:

Általános relativitáselmélet

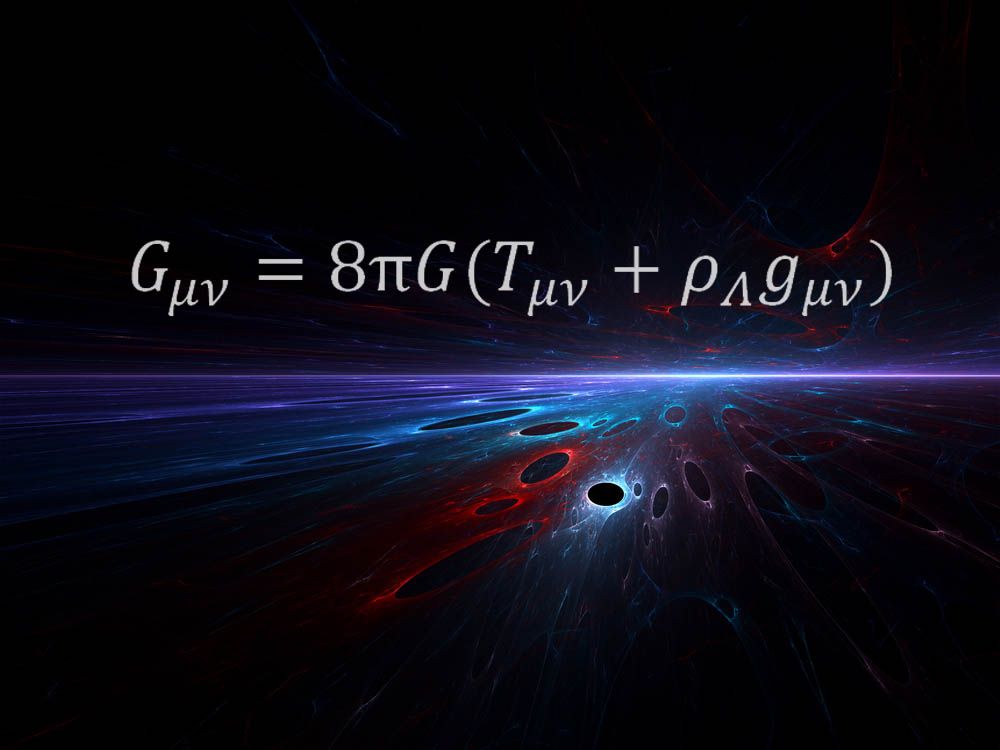
A fenti egyenlet által megfogalmazott Einstein részeként az úttörő általános relativitáselmélet 1915-ben. Az elmélet forradalmasította, hogy a tudósok hogyan értették meg a gravitációt azáltal, hogy az erőt a tér és az idő szövetének csavarásaként írták le.

“számomra még mindig elképesztő, hogy egy ilyen matematikai egyenlet leírhatja, hogy mi a téridő” – mondta az űrteleszkóp Tudományos Intézet asztrofizikusa, Mario Livio, aki az egyenletet kedvencének nevezte. “Einstein valódi zsenialitása ebben az egyenletben testesül meg.”

” ennek az egyenletnek a jobb oldala leírja univerzumunk energiatartalmát (beleértve a “sötét energiát”, amely a jelenlegi kozmikus gyorsulást hajtja) ” -magyarázta Livio. “A bal oldal a téridő geometriáját írja le. Az egyenlőség azt tükrözi, hogy Einstein általános relativitásában a tömeg és az energia határozza meg a geometriát, és egyben a görbületet is, ami az úgynevezett gravitáció megnyilvánulása.”

“Ez egy nagyon elegáns egyenlet” – mondta Kyle Cranmer, a New York-i Egyetem fizikusa, hozzátéve, hogy az egyenlet feltárja a tér-idő és az anyag és az energia kapcsolatát. “Ez az egyenlet megmutatja, hogyan kapcsolódnak egymáshoz — hogyan torzítja a nap jelenléte a téridőt, hogy a Föld körül mozogjon a pályán stb. Azt is elmondja, hogyan fejlődött az univerzum az Ősrobbanás óta, és azt jósolja, hogy fekete lyukaknak kell lenniük.”

A Standard Modell

a fizika egyik uralkodó elmélete, a standard modell leírja az univerzumunkat alkotó alapvető részecskék gyűjteményét.

Az elmélet zárás egy fő egyenlet úgynevezett standard modell Lagrange (a neve után a 18 századi francia matematikus, csillagász, Joseph Louis Lagrange), ami által választott elméleti fizikus Lance Dixon a SLAC Nemzeti Gyorsító Laboratórium Kaliforniában, mint a kedvenc képlet.

“sikeresen leírta a laboratóriumban eddig megfigyelt összes elemi részecskét és erőt — a gravitáció kivételével -” – mondta Dixon a LiveScience-nek. “Ez magában foglalja természetesen a nemrégiben felfedezett Higgs (hasonló) bozont, a phi-t a képletben. Teljesen önálló a kvantummechanika és a speciális relativitáselmélet.”

a standard modellelmélet még nem egyesült az Általános relativitással, ezért nem tudja leírni a gravitációt.

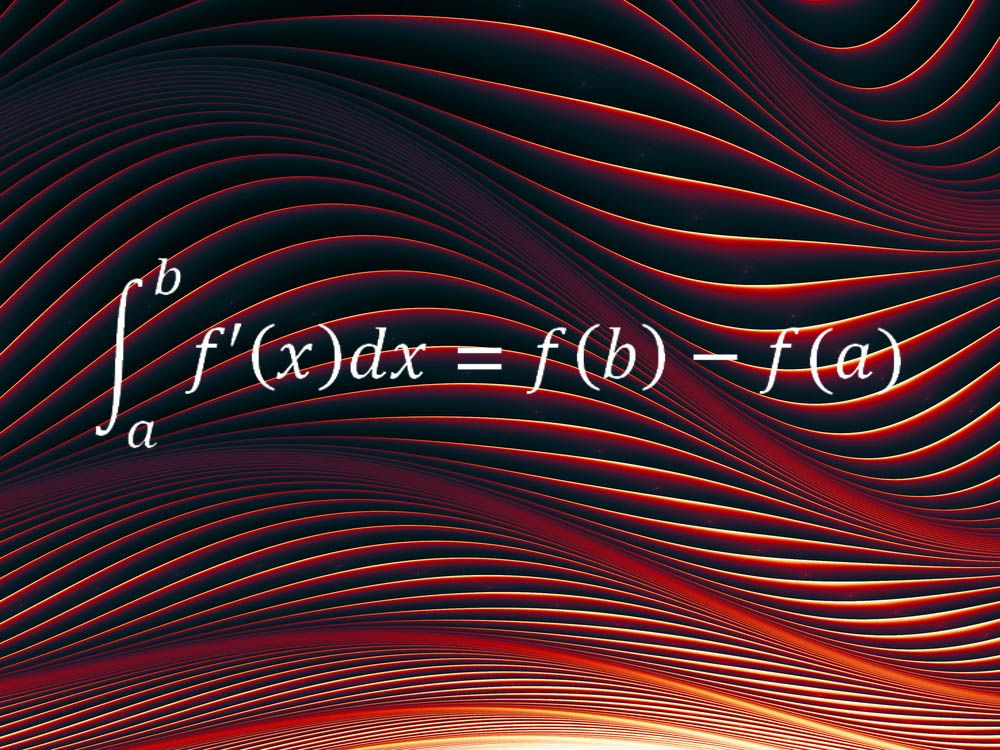
míg az első két egyenlet az univerzum bizonyos aspektusait írja le, egy másik kedvenc egyenlet alkalmazható mindenféle helyzetre. A kalkulus alaptétele képezi a kalkulus néven ismert matematikai módszer gerincét, és összekapcsolja két fő gondolatát, az integrál fogalmát és a származék fogalmát.

“egyszerű szavakkal azt mondja, hogy egy sima és folyamatos mennyiség nettó változása, például egy megtett távolság, egy adott időintervallumban (azaz a mennyiség értékeinek különbsége az időintervallum végpontjaiban) megegyezik az adott mennyiség változási sebességének integráljával, azaz a sebesség integráljával ” -mondta Melkana Brakalova-Trevithick, a Fordham Egyetem Matematikai Tanszékének elnöke, aki ezt az egyenletet választotta kedvencének. “A kalkulus alapvető tétele (FTC) lehetővé teszi számunkra, hogy meghatározzuk a nettó változást egy intervallumban a teljes intervallum változási sebessége alapján.”

a kalkulus magjai az ókorban kezdődtek, de nagy részét a 17.században Isaac Newton állította össze, aki kalkulust használt a Nap körüli bolygók mozgásának leírására.

Pitagorasz-tétel

egy” régi, de jó ” egyenlet a híres pitagorai tétel, amelyet minden kezdő geometria hallgató megtanul.

Ez a képlet azt írja le, hogy minden derékszögű háromszög esetében a hipotenusz hosszának négyzete, c, (a derékszögű háromszög leghosszabb oldala) megegyezik a másik két oldal hosszának négyzetének összegével (a és b). Így a^2 + b^2 = C^2

“az első matematikai tény, amely lenyűgözött, a pitagorai tétel volt” – mondta Daina Taimina matematikus a Cornell Egyetemen. “Akkor még gyerek voltam, és olyan csodálatosnak tűnt számomra, hogy geometriában működik, számokkal működik!”

1 = 0, 999999999….

Ez az egyszerű egyenlet, amely kimondja, hogy a mennyiség 0,999, majd egy végtelen sor kilences, egyenértékű egy, a kedvenc matematikus Steven strogatz Cornell Egyetem.

“szeretem, hogy milyen egyszerű — mindenki megérti, mit mond – mégis milyen provokatív” – mondta Strogatz. “Sokan nem hiszik, hogy ez igaz lehet. Ez is gyönyörűen kiegyensúlyozott. A bal oldal a matematika kezdetét jelenti; a jobb oldal a végtelenség titkait képviseli.”

Speciális relativitás

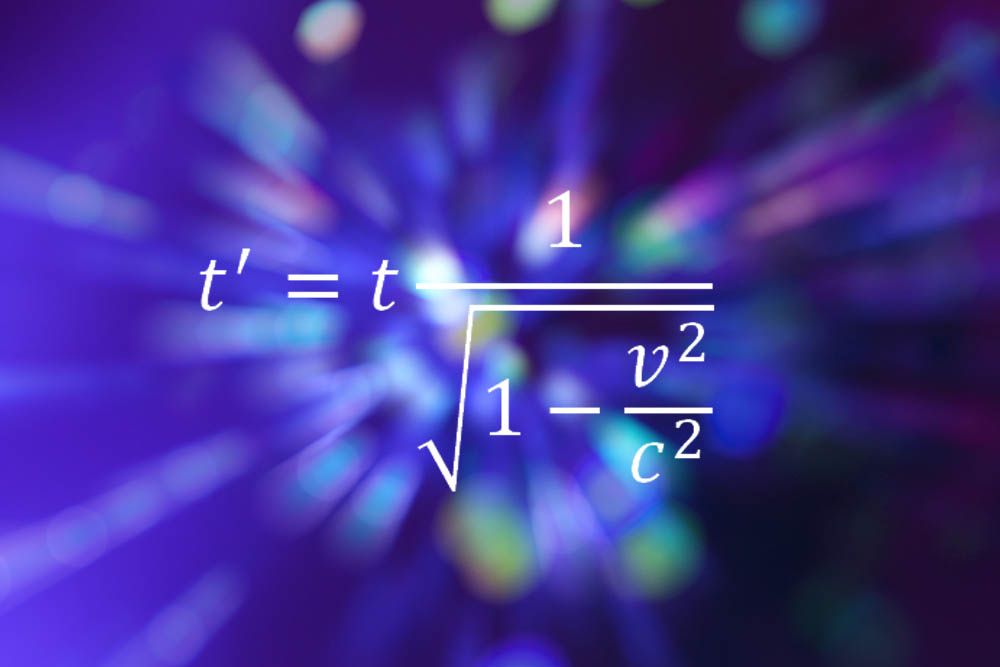
Einstein teszi a listát újra a képletek speciális relativitáselmélet, amely leírja, hogy a tér-idő nem abszolút fogalom, de inkább relatív, attól függően, hogy a sebesség a megfigyelő. A fenti egyenlet azt mutatja, hogy az idő kitágul, vagy lelassul, annál gyorsabban mozog az ember bármely irányba.

“a lényeg az, hogy nagyon egyszerű” – mondta Bill Murray, a Genfi CERN laboratórium részecskefizikusa. “Nincs semmi, amit egy A-szintű hallgató nem tehetne meg, nincs összetett származék és nyomon követhető algebrák. De amit megtestesít, az egy teljesen új módja annak, hogy megnézzük a világot, a valósághoz való hozzáállást és az ahhoz való viszonyunkat. Hirtelen a merev, változatlan kozmoszt elsöpörjük, és egy olyan személyes világ váltja fel, amely az Ön által megfigyelthez kapcsolódik. Az univerzumon kívülről lefelé nézve az egyik összetevőre mozog. De a fogalmakat és a matematikát bárki megragadhatja, aki akar.”

Murray azt mondta, hogy a speciális relativitási egyenleteket részesíti előnyben az Einstein későbbi elméletének bonyolultabb képleteivel szemben. “Soha nem tudtam követni az általános relativitáselmélet matematikáját” – mondta.

Euler egyenlete

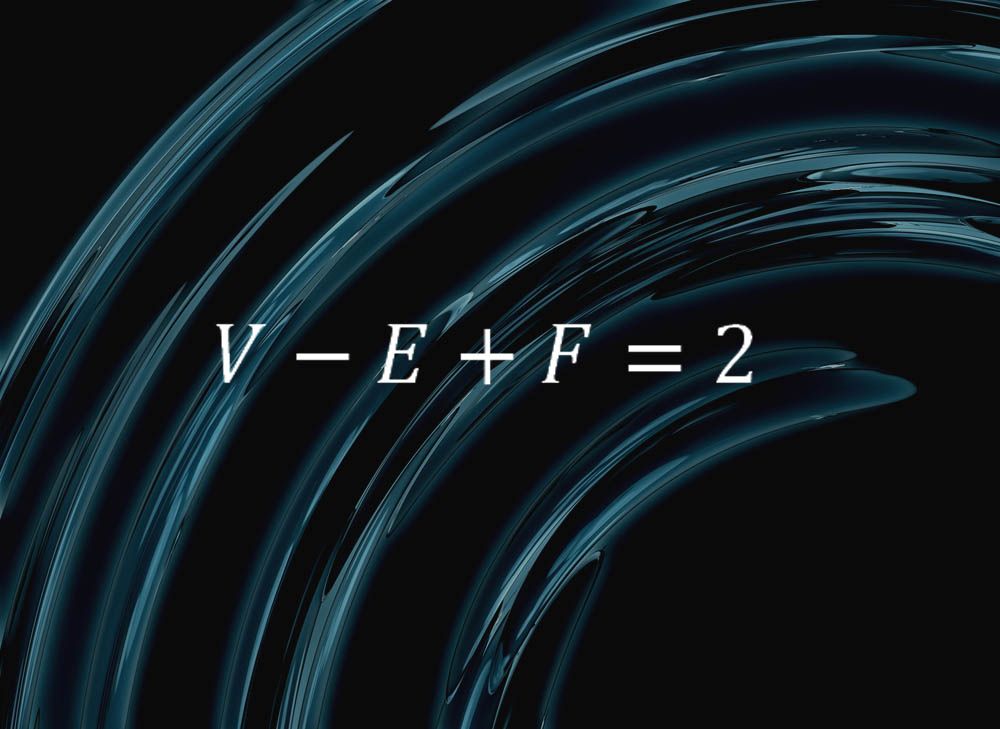
Ez az egyszerű képlet magában foglalja valami tiszta jellegét gömbök:

“azt mondja, hogy ha egy gömb felületét arcokra, szélekre és csúcsokra vágja, és hagyja, hogy F legyen az arcok száma, E az élek száma és V A csúcsok száma, akkor mindig V – E + F = 2 lesz” – mondta Colin Adams, a Massachusetts-i Williams College matematikusa.

“így például Vegyünk egy tetraédert, amely négy háromszögből, hat élből és négy csúcsból áll” – magyarázta Adams. “Ha egy rugalmas arcú tetraéderbe fújtál keményen, akkor gömbre kerekítheted, így ebben az értelemben egy gömböt négy arcra, hat élre és négy csúcsra lehet vágni. És látjuk, hogy V-E + F = 2. Ugyanez vonatkozik az öt arcú piramisra – négy háromszög, egy négyzet – nyolc él és öt csúcs”, valamint az arcok, élek és csúcsok bármely más kombinációjára.

” nagyon jó tény! A csúcsok, szélek és arcok kombinatorikája valami nagyon alapvető dolgot rögzít a gömb alakjában ” – mondta Adams.

Euler-Lagrange-egyenletek és Noether-tétel

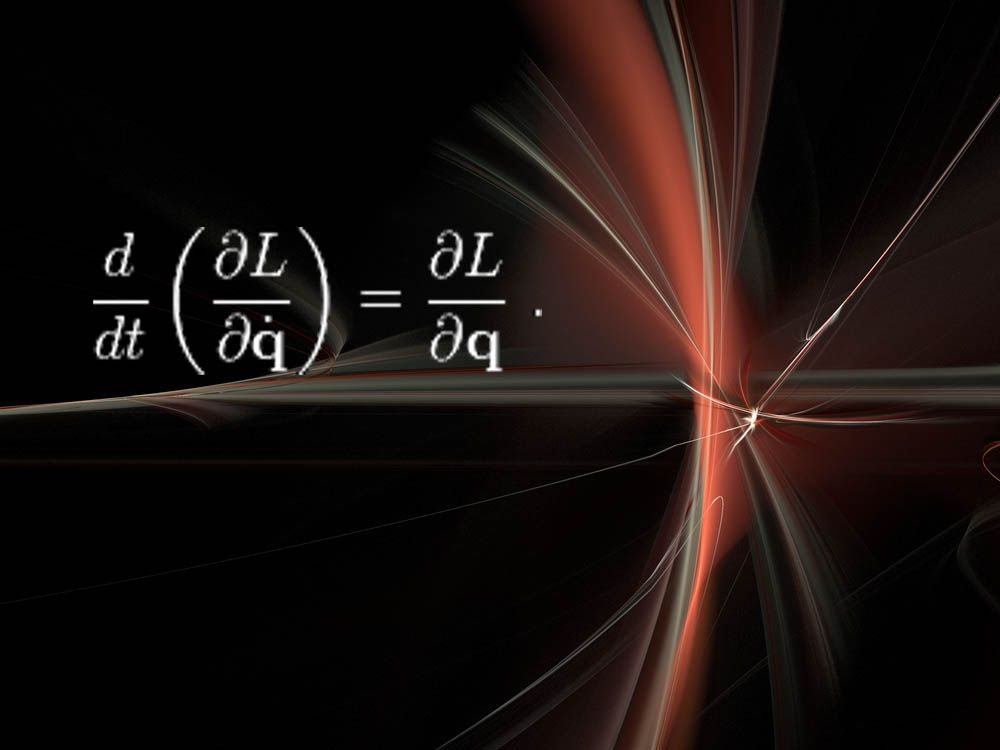
“ezek nagyon elvontak, de elképesztően erősek” – mondta NYU Cranmer. “A hűvös dolog az, hogy ez a fizika gondolkodásmód túlélte a fizika néhány nagy forradalmát, mint például a kvantummechanika, a relativitáselmélet stb.”

itt az L A Lagrangian, amely egy fizikai rendszer energiájának mértéke, például rugók, karok vagy alapvető részecskék. “Ennek az egyenletnek a megoldása megmutatja, hogyan fog fejlődni a rendszer az idővel” – mondta Cranmer.

a Lagrangiai egyenlet spinoffját Noether tételének nevezik, a 20. századi német matematikus, Emmy Noether után. “Ez a tétel valóban alapvető fontosságú a fizika és a szimmetria szerepe szempontjából” – mondta Cranmer. “Informálisan a tétel az, hogy ha a rendszer szimmetriája van, akkor van egy megfelelő védelmi törvény. Például az a gondolat, hogy a fizika alapvető törvényei ma ugyanazok, mint a holnap (idő szimmetriája), azt jelenti, hogy az energia megmarad. Az a gondolat, hogy a fizika törvényei ugyanazok, mint a világűrben, azt jelenti, hogy a lendület megmarad. A szimmetria talán az alapvető fizika vezetési koncepciója, elsősorban a hozzájárulás miatt.”

A Callan-Symanzik egyenlet

“a Callan-a symanzik-egyenlet egy létfontosságú első elvi egyenlet 1970-ből, amely elengedhetetlen annak leírásához, hogy a naiv elvárások hogyan fognak kudarcot vallani egy kvantumvilágban” – mondta Matt strassler, a Rutgers Egyetem elméleti fizikusa.

az egyenletnek számos alkalmazása van, többek között lehetővé téve a fizikusok számára, hogy megbecsüljék az atommagokat alkotó proton és neutron tömegét és méretét.

alapvető fizika azt mondja, hogy a gravitációs erő, valamint az elektromos erő, két tárgy között arányos a négyzet közötti távolság inverzével. Egyszerű szinten ugyanez igaz az erős nukleáris erőre is, amely a protonokat és a neutronokat egymáshoz köti, hogy az atomok magjait képezzék, és amely a kvarkokat egymáshoz köti, hogy protonokat és neutronokat képezzen. Az apró kvantumingadozások azonban kissé megváltoztathatják az erő távolságtól való függését, ami drámai következményekkel jár az erős nukleáris erőre.

“Ez megakadályozza, hogy ez az erő nagy távolságokon csökkenjen, és arra készteti, hogy csapdába ejtse a kvarkokat, és összekapcsolja őket, hogy világunk protonjait és neutronjait képezzék” – mondta Strassler. “Amit a Callan-Symanzik egyenlet tesz, az a drámai és nehezen kiszámítható hatás, amely akkor fontos, ha nagyjából egy proton mérete, finomabb, de könnyebben kiszámítható hatásokhoz kapcsolódik, amelyek akkor mérhetők, ha sokkal kisebb, mint egy proton.”

A minimális felület egyenlet

“A minimális felület egyenlet valahogy kódolja a gyönyörű szappan filmek formában vezeték határokat, amikor mártsuk szappanos víz,”azt mondta, matematikus Frank Morgan a Williams Főiskola. “Az a tény, hogy az egyenlet “nemlineáris”, amely a származékok erejét és termékeit foglalja magában, a szappanfilmek meglepő viselkedésének kódolt matematikai utalása. Ez ellentétben áll az ismertebb lineáris parciális differenciálegyenletekkel, mint például a hőegyenlet, a hullámegyenlet, valamint a kvantumfizika Schrödinger egyenlete.”