9.4: ionos kötés
Ionos Kötésképződés energetikája
ionos kötések keletkeznek, amikor a pozitív és negatív töltésű ionokat elektrosztatikus erők tartják össze. Tekintsünk egy pár iont, egy kationot és egy anionot. Mennyire lesz erős vonzerejük ereje? A Coulomb törvénye szerint a két töltött részecske közötti elektrosztatikus vonzerő (\(E\) energiája arányos a töltések nagyságával, fordítottan arányos a részecskék közötti internukleáris távolsággal (\(r\)):
\
\
ahol minden ion töltését Q szimbólum képviseli. a K arányossági állandó egyenlő 2,31 × 10-28 J·M. Ez a K érték magában foglalja az egyes ionokra vonatkozó egyetlen elektron töltését (1,6022 × 10-19 C). Az egyenletet az egyes ionok töltésével is meg lehet írni, coulombokban (C) kifejezve, beépítve az állandóba. Ebben az esetben az arányossági állandó, k, 8, 999 × 109 J·m/C2. A megadott példában Q1 = +1 (1,6022 × 10-19 C) és Q2 = -1 (1,6022 × 10-19 C). Ha Q1, majd Q2 ellentétes jelek (mint NaCl, például, ahol Q1 +1 Na+, illetve a K2 az -1 a Cl−), akkor E negatív, ami azt jelenti, hogy energia szabadul fel, ha ellentétes töltésű ionok hozott össze a végtelen távolság, hogy alkotnak egy elszigetelt ion-pár.
az energia mindig felszabadul, amikor kötés alakul ki, és ennek megfelelően mindig energiát igényel a kötés megtöréséhez.
amint azt a \ábra alsó felében lévő zöld görbe mutatja(\PageIndex{1}\), A maximális energia akkor szabadul fel, ha az ionok végtelenül közel vannak egymáshoz, r = 0-nál. Mivel az ionok helyet foglalnak el és szerkezetük olyan, hogy a pozitív magot elektronok veszik körül, azonban nem lehetnek végtelenül közel egymáshoz. Nagyon rövid távolságokon a szomszédos ionokon lévő elektronok közötti visszataszító elektron–elektron kölcsönhatások erősebbé válnak, mint az ellentétes töltésű ionok közötti vonzó kölcsönhatások, amint azt a \ ábra felső felében található piros görbe mutatja (\PageIndex{1}\). A rendszer teljes energiája egyensúly a vonzó és visszataszító kölcsönhatások között. A \(\PageIndex{1}\) ábrán látható lila görbe azt mutatja, hogy a rendszer teljes energiája eléri a minimumot r0-nál, ahol az elektrosztatikus taszítások és látványosságok pontosan kiegyensúlyozottak. Ez a távolság megegyezik a kísérletileg mért kötési távolsággal.
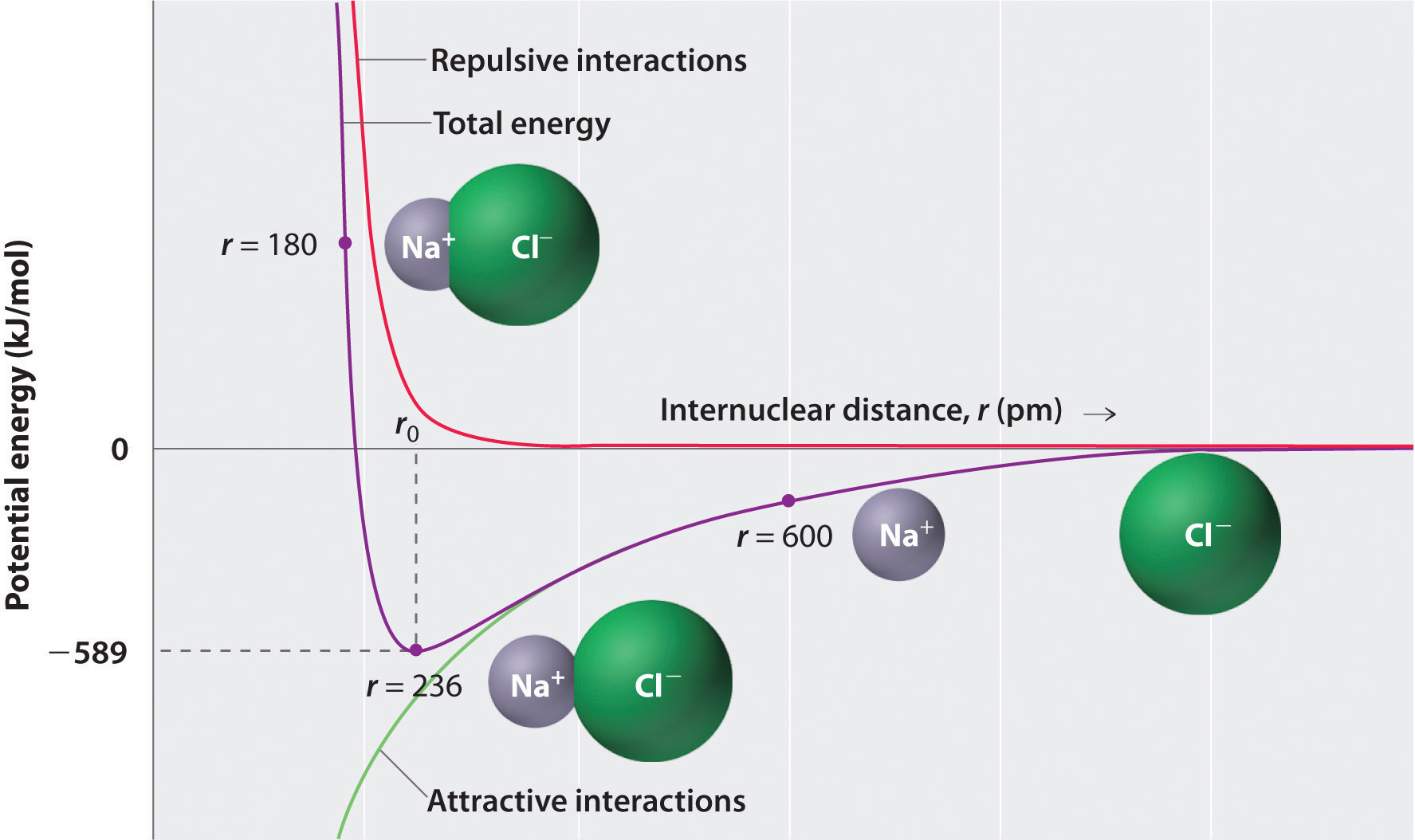
fontolja meg a felszabaduló energiát, amikor egy gáznemű \(Na^+\) ion és egy gáznemű \(Cl^-\) ion R = ∞ – ről r = r0-ra kerül. Tekintettel arra, hogy a megfigyelt gáz fázisú internuclear távolság 236 pm, az energia változás kapcsolódó kialakulását egy ion-pár egy \(Na^+_{(g)}\) – ion, valamint a \(Cl^-_{(g)}\) ion a következők:
\ &= (2.31 \alkalommal {10^{ – 28}}\rm{J}\cdot \mégse{m} ) \left( \dfrac{( + 1)( – 1)}{236\; \mégse{pm} \alkalommal 10^{ – 12} \mégse{m/pm -}} \right) \\ &= – 9.79 \times 10^ {- 19}\; J / ion\; pair \ label{EQ2} \ end{align*}\]
a negatív érték azt jelzi, hogy az energia felszabadul. Egyezményünk az, hogy ha egy kémiai folyamat energiát biztosít a külvilág számára, az energiaváltás negatív. Ha energiát igényel, az energiaváltás pozitív. A NaCl Párok móljának kialakulásában bekövetkező energiaváltozás kiszámításához meg kell szoroznunk az ionpáronkénti energiát az Avogadro számával:
\
Ez az az energia, amely akkor szabadul fel, amikor 1 mol gáz halmazállapotú ionpár keletkezik, nem akkor, amikor 1 mol pozitív és negatív ionok kondenzálódnak kristályrács formájában. A rácsszerkezet hosszú távú kölcsönhatásai miatt ez az energia nem felel meg közvetlenül a kristályos szilárd anyag rácsos energiájának. A nagy negatív érték azonban azt jelzi, hogy a pozitív és negatív ionok összekapcsolása energetikailag nagyon kedvező, akár ionpár, akár kristályrács alakul ki.
összefoglaljuk az ionos kötéssel kapcsolatos fontos pontokat:
- az R0-nál az ionok stabilabbak (alacsonyabb potenciális energiával rendelkeznek), mint végtelen internukleáris távolságban. Amikor az ellentétes töltésű ionokat r = ∞ – ről r = r0-ra állítják össze, a rendszer energiája csökken (az energia felszabadul).
- az R0 alacsony potenciális energiája miatt energiát kell hozzáadni a rendszerhez az ionok elválasztásához. A szükséges energia mennyisége a kötési energia.
- a rendszer energiája eléri a minimumot egy adott internukleáris távolságon (a kötési távolság).
példa \ (\PageIndex{2}\): LiF
Számítsa ki a felszabaduló energia mennyiségét, amikor az elválasztott ionokból 1 mol gáznemű Li+F− ion pár alakul ki. A gázfázisban megfigyelt internukleáris távolság 156 pm.
Adott: kation, illetve anion, összeg, valamint internuclear távolság
Kért: energia szabadul fel kialakulását gáz-halmazállapotú ion pár
Stratégia:
Helyettesíti a megfelelő értékeket Egyenlet \(\ref{Eq1b}\), hogy megszerezze a felszabaduló energia a kialakulását egyetlen ion-pár, majd szorozza meg ezt az értéket az Avogadro-szám, hogy az energiát, megjelent egy tégla.
megoldás:
Behelyezése az értékek Li+F− be Egyenlet \(\ref{Eq1b}\) (ahol Q1 = +1, Q2 = -1, illetve r = 156 pm), azt találjuk, hogy az energia társul a kialakulását egyetlen pár Li+F− ionok
\ &=\left(2.31 \alkalommal 10^{-28} J⋅\mégse{m} \right) \left(\dfrac{\szöveget{(+1)(-1)}}{156\; pm \alkalommal 10^{-12} \mégse{m/pm -}} \right)\\ &=-1.48 \alkalommal 10^{-18} \end{align*}\]
Akkor a felszabaduló energia per tégla Li+F− ion párok
\ &-891 \;kJ / mol \ end{align*}\]
mivel a Li + és az F-kisebb, mint a Na+ és a Cl – (lásd 7.3 pont), a LiF-ben az internukleáris távolság rövidebb, mint a NaCl-ben. Következésképpen a \(\ref{eq1b}\) egyenletnek megfelelően sokkal több energia szabadul fel, ha 1 mol gáznemű Li + F-ion pár képződik (-891 kJ / mol), mint amikor 1 mol gáznemű Na+Cl− ion pár képződik (-589 kJ/mol).
Exercise \ (\PageIndex{2}\): magnézium-oxid
Számítsa ki a felszabaduló energia mennyiségét, amikor 1 mol gáz halmazállapotú \(\ce{MgO}\) ionpár alakul ki az elválasztott ionokból. A gázfázis internukleáris távolsága 175 pm.
válasz
-3180 kJ / mol = -3,18 × 103 kJ/mol
Leave a Reply