kérjük, adjon meg vesszővel elválasztott számokat a számításhoz.

kapcsolódó statisztikai számológép / szórás kalkulátor / Minta Méret kalkulátor

átlag

a szó jelentése, amely több más szó homonimája az angol nyelven, hasonlóan kétértelmű, még a matematika területén is. A kontextustól függően, legyen az matematikai vagy statisztikai, mit jelent az “átlag” változás. Az adatkészletekre vonatkozó legegyszerűbb matematikai definíciójában az alkalmazott átlag az aritmetikai átlag, amelyet matematikai elvárásnak vagy átlagnak is neveznek. Ebben a formában az átlag egy diszkrét számkészlet közötti közbenső értékre utal, nevezetesen az adatkészletben lévő összes érték összegére, osztva az értékek teljes számával. Az aritmetikai átlag kiszámításának egyenlete gyakorlatilag megegyezik a populáció és a minta átlagának statisztikai fogalmainak kiszámításával, az alkalmazott változók enyhe változásával:

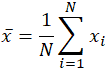
az átlagot gyakran x-ként jelölik, “x bar” – nak ejtik, és még más felhasználásokban is, ha a változó nem x, a sávjelzés az átlag valamilyen formájának közös mutatója. A populáció konkrét esetben az x változó használata helyett a görög Mu vagy μ szimbólumot használják. Hasonlóképpen, vagy inkább zavaróan, a statisztikákban szereplő minta átlagát gyakran x tőkével jelölik. Tekintettel az adathalmazra 10, 2, 38, 23, 38, 23, 21, a hozamok feletti összeg alkalmazása:

Mint már korábban említettük, ez az egyik legegyszerűbb meghatározása az jelenti, hogy az, mások közé tartozik a súlyozott számtani közép (ami csak abban különbözik, hogy bizonyos értékek a felsorolt adatok hozzájárulnak ahhoz, több érték, mint a többiek), valamint a mértani közép. Az adott helyzetek és kontextusok megfelelő megértése gyakran biztosítja a személy számára a szükséges eszközöket annak meghatározásához, hogy milyen statisztikailag releváns módszert kell használni. Általánosságban azt jelenti, medián, módját, illetve tartomány ideális esetben minden számítani, illetve elemezték, egy adott minta vagy adat állítani, mivel ők tudósított a különböző aspektusai a megadott adatokat, ha figyelembe egyedül, oda vezethet, hogy a félrevezetés az adatok, mint kerül bemutatásra az alábbiakban.

medián

a medián statisztikai fogalma olyan érték, amely egy adatmintát, populációt vagy valószínűségi eloszlást két részre oszt. A medián megtalálása lényegében magában foglalja az érték megtalálását egy olyan adatmintában, amelynek fizikai helye van a többi szám között. Ne feledje, hogy a számok véges listájának mediánjának kiszámításakor fontos az adatminták sorrendje. Hagyományosan az értékek növekvő sorrendben vannak felsorolva, de nincs valódi oka annak, hogy az értékek csökkenő sorrendben történő felsorolása eltérő eredményeket eredményezne. Abban az esetben, ha egy adatmintában az értékek teljes száma páratlan, a medián egyszerűen az összes érték listájának közepén lévő szám. Ha az adatminta páros számú értéket tartalmaz, a medián a két középső érték átlaga. Bár ez zavaró lehet, egyszerűen ne feledje, hogy annak ellenére, hogy a medián néha magában foglalja az átlag kiszámítását, amikor ez az eset felmerül, csak a két középső értéket foglalja magában, míg az átlag az adatmintában szereplő összes értéket tartalmazza. Azokban a páratlan esetekben, amikor csak két adatminta van, vagy páros számú minta van, ahol az összes érték azonos, az átlag és a medián azonos lesz. Mivel ugyanaz az adatkészlet, mint korábban, a medián a következő módon szerezhető be:

2,10,21,23,23,38,38

az adatok növekvő sorrendben történő felsorolása után, és annak meghatározása, hogy páratlan számú érték van, egyértelmű, hogy ebben az esetben 23 a medián. Ha volt egy másik hozzáadott érték az adatkészlethez:

2,10,21,23,23,38,38,1027892

mivel páros számú érték van, a medián a két középső szám átlaga lesz, ebben az esetben 23 és 23, amelynek átlaga 23. Vegye figyelembe, hogy ebben a konkrét adathalmazban egy kiugró (a várható értéktartományon kívüli érték), az 1,027,892 érték hozzáadása nincs valódi hatással az adathalmazra. Ha azonban az átlagot kiszámítják erre az adatkészletre, az eredmény 128,505.875. Ez az érték nyilvánvalóan nem tükrözi jól az adathalmazban található hét másik értéket, amelyek jóval kisebbek és közelebb vannak az átlaghoz és a kiugró értékhez. Ez a fő előnye a medián használatának a statisztikai adatok leírásában az átlaghoz képest. Míg mindkettőt, valamint más statisztikai értékeket is ki kell számítani az adatok leírásakor, ha csak egyet lehet használni, a medián egy adott adatkészletben egy tipikus érték jobb becslését tudja biztosítani, ha az értékek között rendkívül nagy eltérések vannak.

Mode

a statisztikákban az üzemmód az adatkészlet értéke, amely a legtöbb ismétlődést tartalmazza. Lehetséges, hogy egy adatkészlet multimodális legyen, ami azt jelenti, hogy egynél több mód van. Például:

2,10,21,23,23,38,38

mind a 23, mind a 38 kétszer jelenik meg, így mindkettő a fenti adatkészlet módja.

az átlaghoz és a mediánhoz hasonlóan az üzemmódot használják a véletlenszerű változókra és populációkra vonatkozó információk kifejezésére. Az átlagtól és a medián értéktől eltérően azonban az üzemmód olyan fogalom, amely nem numerikus értékekre alkalmazható, mint például a tortilla chips márkája, amelyet leggyakrabban egy élelmiszerboltból vásárolnak. Például, ha összehasonlítjuk a márkák Tostitos, Mission, és XOCHiTL, ha azt találjuk, hogy az értékesítés tortilla chips, XOCHiTL az a mód, és eladja a 3:2:1 arány képest Tostitos és Mission brand tortilla chips illetőleg, az arány lehet használni, hogy meghatározza, hogy hány zsák minden márka raktáron. Abban az esetben, ha egy adott időszak alatt 24 zsák tortilla chipet értékesítenek, az üzlet 12 zsák XOCHiTL chipet, 8 Tostitost és 4 küldetést tárolna az üzemmód használata esetén. Ha azonban a bolt egyszerűen használt egy átlagos és eladott 8 zsák minden, ez potenciálisan elveszíti 4 értékesítés, ha egy ügyfél kívánt csak XOCHiTL chipek, nem pedig bármely más márka. Amint az ebből a példából kitűnik, fontos, hogy a statisztikai értékek minden módját figyelembe vegyük, amikor bármilyen adatmintáról következtetéseket vonunk le.

tartomány

a statisztikai adathalmaz tartománya a legnagyobb és a legkisebb értékek közötti különbség. Míg a tartománynak a statisztika és a matematika különböző területein eltérő jelentése van, ez a legalapvetőbb definíciója, és ezt használja a megadott számológép. Ugyanezt a példát használva:

2,10,21,23,23,38,38
38-2 = 36

ebben a példában a tartomány 36. Az átlaghoz hasonlóan a tartományt jelentősen befolyásolhatják a rendkívül nagy vagy kis értékek. Ugyanaz a példa, mint korábban: