AUC-ROC kurve – stjernen Performer!

du har bygget din machine learning model – så hvad bliver det næste? Du skal evaluere det og validere, hvor godt (eller dårligt) det er, så du kan derefter beslutte, om du vil implementere det. Det er her AUC-ROC-kurven kommer ind.

navnet kan være en mundfuld, men det siger bare, at vi beregner “området under kurven” (AUC) for “modtager karakteristisk operatør” (ROC). Forvirret? Jeg føler dig! Jeg har været i dine sko. Men rolig, vi vil se, hvad disse udtryk betyder i detaljer, og alt vil være et stykke kage!

for nu skal du bare vide, at AUC-ROC-kurven hjælper os med at visualisere, hvor godt vores maskinlæringsklassifikator udfører. Selvom det kun fungerer for binære klassificeringsproblemer, vil vi se mod slutningen, hvordan vi også kan udvide det til at evaluere klassificeringsproblemer i flere klasser.

Vi dækker også emner som følsomhed og specificitet, da disse er nøgleemner bag AUC-ROC-kurven.

Jeg foreslår at gennemgå artiklen om Forvirringsmatrice, da den vil introducere nogle vigtige udtryk, som vi vil bruge i denne artikel.

Indholdsfortegnelse

• hvad er følsomhed og specificitet?
• Sandsynlighed for forudsigelser
• hvad er AUC-ROC-kurven?
• Hvordan virker AUC-ROC-kurven?
• AUC-ROC i Python
• AUC-ROC til klassificering i flere klasser

Hvad er følsomhed og specificitet?

Sådan ser en forvirringsmatrice ud:

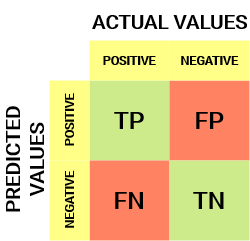
fra forvirringsmatricen kan vi udlede nogle vigtige målinger, der ikke blev diskuteret i den foregående artikel. Lad os tale om dem her.

Sensitivity / True Positive Rate/Recall

Sensitivity fortæller os, hvilken andel af den positive klasse fik korrekt klassificeret.

et simpelt eksempel ville være at bestemme, hvilken andel af de faktiske syge mennesker der blev registreret korrekt af modellen.

falsk negativ Rate

falsk negativ Rate (FNR) fortæller os, hvilken andel af den positive klasse fik forkert klassificeret af klassifikatoren.

en højere TPR og en lavere FNR er ønskelig, da vi ønsker at klassificere den positive klasse korrekt.

specificitet / ægte negativ Rate

specificitet fortæller os, hvilken andel af den negative klasse der blev klassificeret korrekt.

Hvis man tager det samme eksempel som i følsomhed, ville specificitet betyde at bestemme andelen af raske mennesker, der blev identificeret korrekt af modellen.

falsk positiv Rate

FPR fortæller os, hvilken andel af den negative klasse fik forkert klassificeret af klassifikatoren.

en højere TNR og en lavere FPR er ønskelig, da vi ønsker at klassificere den negative klasse korrekt.

ud af disse målinger er følsomhed og specificitet måske den vigtigste, og vi vil senere se, hvordan disse bruges til at opbygge en evalueringsmetrik. Men før det, lad os forstå, hvorfor sandsynligheden for forudsigelse er bedre end at forudsige målklassen direkte.

Sandsynlighed for forudsigelser

en maskinlæringsklassificeringsmodel kan bruges til at forudsige den faktiske klasse af datapunktet direkte eller forudsige dens sandsynlighed for at tilhøre forskellige klasser. Sidstnævnte giver os mere kontrol over resultatet. Vi kan bestemme vores egen tærskel for at fortolke resultatet af klassifikatoren. Dette er nogle gange mere forsigtigt end bare at bygge en helt ny model!

Indstilling af forskellige tærskler for klassificering af positiv klasse for datapunkter vil utilsigtet ændre modelens følsomhed og specificitet. Og en af disse tærskler vil sandsynligvis give et bedre resultat end de andre, afhængigt af om vi sigter mod at sænke antallet af falske negativer eller falske positiver.

se nedenstående tabel:

målingerne ændres med de skiftende tærskelværdier. Vi kan generere forskellige forvirringsmatricer og sammenligne de forskellige målinger, som vi diskuterede i det foregående afsnit. Men det ville ikke være en forsigtig ting at gøre. I stedet kan vi generere et plot mellem nogle af disse målinger, så vi nemt kan visualisere, hvilken tærskel der giver os et bedre resultat.

AUC-ROC-kurven løser netop det problem!

hvad er AUC-ROC-kurven?

kurven for Modtageroperatørkarakteristika (Roc) er en evalueringsmetrik for binære klassificeringsproblemer. Det er en sandsynlighedskurve, der tegner TPR mod FPR ved forskellige tærskelværdier og i det væsentlige adskiller ‘signalet’ fra ‘støj’. Området under kurven (AUC) er mål for en klassificerings evne til at skelne mellem klasser og bruges som en oversigt over ROC-kurven.

jo højere AUC, desto bedre er præstationen af modellen ved at skelne mellem de positive og negative klasser.

når AUC = 1, er klassifikatoren i stand til perfekt at skelne mellem alle de Positive og de Negative klassepunkter korrekt. Hvis, imidlertid, AUC havde været 0, så klassifikatoren ville forudsige alle negativer som positive, og alle positive som negative.

Når 0.5 <AUC< 1, der er stor chance for, at klassifikatoren vil kunne skelne de positive klasseværdier fra de negative klasseværdier. Dette skyldes, at klassifikatoren er i stand til at opdage flere antal sande positive og sande negativer end falske negativer og falske positive.

når AUC=0,5, er klassifikatoren ikke i stand til at skelne mellem Positive og Negative klassepunkter. Betydning enten klassifikatoren forudsiger tilfældig klasse eller konstant klasse for alle datapunkter.

så jo højere AUC-værdien for en klassifikator er, desto bedre er dens evne til at skelne mellem positive og negative klasser.

Hvordan virker AUC-ROC-kurven?

i en ROC-kurve angiver en højere Akseværdi et højere antal falske positiver end sande negativer. Mens en højere y-akseværdi indikerer et højere antal sande positive end falske negativer. Så valget af tærsklen afhænger af evnen til at balancere mellem falske positive og falske negativer.

lad os grave lidt dybere og forstå, hvordan vores ROC-kurve ville se ud for forskellige tærskelværdier, og hvordan specificiteten og følsomheden ville variere.

Vi kan prøve at forstå denne graf ved at generere en forvirringsmatrice for hvert punkt svarende til en tærskel og tale om udførelsen af vores klassifikator:

punkt A er hvor følsomheden er den højeste og specificiteten den laveste. Dette betyder, at alle de Positive klassepunkter klassificeres korrekt, og at alle de Negative klassepunkter klassificeres forkert.

faktisk svarer ethvert punkt på den blå linje til en situation, hvor ægte positiv sats er lig med falsk positiv sats.

alle punkter over denne linje svarer til den situation, hvor andelen af korrekt klassificerede punkter, der tilhører den Positive klasse, er større end andelen af forkert klassificerede punkter, der tilhører den Negative klasse.

selvom punkt B har samme følsomhed som punkt A, har den en højere specificitet. Det betyder, at antallet af forkert Negative klassepunkter er lavere sammenlignet med den foregående tærskel. Dette indikerer, at denne tærskel er bedre end den foregående.

mellem punkterne C og D er følsomheden ved punkt C højere end punkt D for den samme specificitet. Dette betyder, for det samme antal forkert klassificerede Negative klassepunkter, klassifikatoren forudsagde et højere antal Positive klassepunkter. Derfor er tærsklen ved punkt C bedre end punkt D.

nu, afhængigt af hvor mange forkert klassificerede punkter vi vil tolerere for vores klassifikator, ville vi vælge mellem punkt B eller C for at forudsige, om du kan besejre mig i PUBG eller ej.

” falske forhåbninger er farligere end frygt.”- J. R. R. Tolkein

punkt E er hvor specificiteten bliver højest. Betydning der er ingen falske positiver klassificeret efter modellen. Modellen kan korrekt klassificere alle de Negative klassepunkter! Vi ville vælge dette punkt, hvis vores problem var at give perfekte sanganbefalinger til vores brugere.

Når du følger denne logik, kan du gætte, hvor det punkt, der svarer til en perfekt klassifikator, ville ligge på grafen?

Ja! Det ville være i øverste venstre hjørne af ROC-grafen svarende til koordinaten (0, 1) i det kartesiske plan. Det er her, at både følsomhed og specificitet ville være den højeste, og klassifikatoren ville korrekt klassificere alle de Positive og Negative klassepunkter.

forståelse af AUC-ROC-kurven i Python

nu kan vi enten manuelt teste følsomheden og specificiteten for hver tærskel eller lade sklearn gøre jobbet for os. Vi går helt sikkert med sidstnævnte!

lad os oprette vores vilkårlige data ved hjælp af sklearn make_classification-metoden:

Jeg vil teste udførelsen af to klassifikatorer på dette datasæt:

Sklearn har en meget potent metode roc_curve (), som beregner ROC for din klassifikator i løbet af få sekunder! Det returnerer FPR -, TPR-og tærskelværdierne:

AUC-score kan beregnes ved hjælp af roc_auc_score () – metoden til sklearn:

0.9761029411764707 0.9233769727403157

prøv denne kode i vinduet live coding nedenfor:

Vi kan også plotte ROC-kurverne for de to algoritmer ved hjælp af matplotlib:

det fremgår af plottet, at AUC for den logistiske Regressions ROC-kurve er højere end den for KNN ROC-kurven. Derfor kan vi sige, at logistisk regression gjorde et bedre stykke arbejde med at klassificere den positive klasse i datasættet.

AUC-ROC til klassificering i flere klasser

som jeg sagde før, er AUC-ROC-kurven kun til binære klassificeringsproblemer. Men vi kan udvide det til multiklasseklassificeringsproblemer ved at bruge One vs All-teknikken.

så hvis vi har tre klasser 0, 1 og 2, genereres ROC for klasse 0 som klassificering 0 mod ikke 0, dvs.1 og 2. ROC for klasse 1 vil blive genereret som klassificering 1 mod ikke 1 osv.

ROC-kurven for klassificeringsmodeller i flere klasser kan bestemmes som nedenfor:

slutnoter

Jeg håber, du fandt denne artikel nyttig til at forstå, hvor kraftig AUC-ROC-kurvemetrikken er til måling af en klassificerings ydeevne. Du vil bruge dette meget i branchen og endda inden for datalogi eller maskinlæring hackathons. Bedre blive fortrolig med det!

gå videre Jeg vil anbefale dig følgende kurser, der vil være nyttige til at opbygge din datavidenskabelige skarphed:

• Introduktion til datavidenskab
• anvendt maskinlæring

du kan også læse denne artikel på vores mobilapp