4-farveproblemet er et af de mest berømte matematiske problemer. Det modstod bevis i mere end hundrede år, før det endelig bukkede under; til sidst var der et gyldigt bevis, men et, der stod på mere end tusind timers computertid. Jim Tilleys forskning tyder på, at en dramatisk forenkling i sidste ende kan være mulig. Han har opdaget en ejendom, Kempe-låsning, at et minimum modeksempel til 4-farve sætningen skal udvise og har formuleret en formodning, baseret på omfattende undersøgelser, at Birkhoff-diamanten er den eneste grundlæggende Kempe-låsning konfiguration.

Graffarvning involverer tildeling af etiketter eller farver til hjørnerne af et matematisk objekt kendt som en graf. 4-farveproblemet gav en af de oprindelige motivationer for udviklingen af algebraisk grafteori. Graffarvning bruges i mange virkelige problemer, såsom minimering af konflikter ved planlægning af sportsbegivenheder, planlægning af eksamensplaner og organisering af siddepladser, selv til CCTV-kameraplacering i en bygning med mange hjørner for at minimere overlapning af kameraet. Det giver også grundlaget for Sudoku puslespil.

4-farveproblemet
Francis Guthrie, en studerende af den berømte britiske matematiker og logiker Augustus De Morgan, udgjorde 4-farveproblemet i 1852. Han formulerede problemet med hensyn til kort, der opfylder visse betingelser, såsom ikke at indeholde huller og have hver region (f.eks. land eller stat) forbundet, så der ikke findes nogen region i to eller flere ikke-sammenhængende dele. Guthrie hævdede, at det for sådanne kort aldrig ville tage mere end fire farver at farve kortet, så ingen to naboregioner havde samme farve.

i dag udtrykkes 4-farveproblemet i form af grafer, og i stedet for at farve regioner i kort, farver man hjørner i grafer. Alle eksisterende beviser for 4-farve sætningen viser, at et minimum modeksempel ikke kan eksistere. (Et minimum modeksempel er den mindste plane graf, der kræver mere end fire farver for en korrekt farvning af dens hjørner.) Kun plane grafer, der er trianguleringer, skal overvejes, da enhver graf, der ikke er en triangulering, kan omdannes til en ved at indsætte kanter. Hvis den resulterende triangulering er 4-farvet, så er den oprindelige graf også 4-farvet. Det er meget nyttigt at kunne begrænse sin kontrol til trianguleringer.

et tidligt forsøg på bevis
af dem, der tilbød et bevis, Alfred Bray Kempe, en engelsk advokat og amatørmatematiker, var den person, hvis omdømme var mest plettet af hans mislykkede indsats. Han annoncerede sin succes i 1879 og hans’ bevis ‘ blev offentliggjort i American Journal of Mathematics. Elleve år senere skabte en anden engelsk matematiker, Percy, et kort, som han 4-farvede op til den endelige region på en sådan måde, at Kempe ‘ s metode mislykkedes for den endelige region. På trods af hans fiasko forlod Kempe et nyttigt værktøj – en Kempe-kæde. Det er en maksimal, forbundet (hvert toppunkt, der kan nås fra ethvert andet ved en sti langs kanterne) subgraf, hvor alle hjørner bruger nøjagtigt to farver. Kempe-kæder har vist sig at være medvirkende til at farve og genfarve grafer. Se Figur 1.

det ville være en forbløffende forenkling
Hvis Birkhoff-diamanten alene er nøglen til 4-farvelighed.

endelig bevis
det første gyldige bevis blev annonceret i 1976 af Kenneth Appel og Ulvgang Haken. Det krævede over tusind timers computertid at verificere bestemte aspekter af deres argument. Denne forestilling om at stole på computerkode, der potentielt indeholder menneskeskabte fejl (og deres kode gjorde!), snarere end et ‘menneskeligt’ bevis, har ikke opfyldt en stor del af det matematiske samfund. Appel og hakens bevis var elegant i sin overordnede struktur, men detaljerne var grimme. beviset blev raffineret i 1996 af et team på fire matematikere: Robertson, Sanders, Seymour og Thomas, men de stolede stadig på computerkode for at fuldføre deres bevis. I 2010 tilbød Steinberger en anden variation. Der er dog stadig ikke noget helt tilfredsstillende svar på, hvorfor 4-farve sætningen er sand. (Når formodningen blev bevist, fik den status som en ‘ sætning.’)

søgningen efter et alternativt bevis
4-farveproblemet er så let at formulere og forstå, at det har tiltrukket mange tusinde amatørmatematikers interesse, alle tror, at de kan finde et simpelt klassisk bevis og dermed blive berømt. Jim Tilleys far, en fysiker og rektor for Canadas Royal Military College fra 1978-1984, var en sådan drømmer. Hver gang han følte, at han havde gjort et gennembrud, bad han sin søn, Jim, om at kontrollere sit arbejde. Jim fandt altid en fejl. På trods af sin oprindelige skepsis over for, at hans fars indsats nogensinde ville bære frugt, blev han inficeret med en entusiasme for 4-farveproblemet og begyndte at studere det intenst.Jim Tilleys forskning førte til, at han opdagede en ny ejendom, som et minimum modeksempel til 4-farve sætningen skal udvise. Han kaldte det Kempe-locking. Han indså, at det sandsynligvis ville være uforeneligt med en anden ejendom, som et minimum modeksempel skal udstille – nemlig., hvor tilsluttet en graf er (hvor mange hjørner skal fjernes fra en graf, før den falder fra hinanden).Tilleys Kempe-låsning er en egenskab, der er forbundet med en kant i en triangulering. Begrebet starter med at slette en kant mellem tilstødende hjørner og y. Hvis der for hver 4-farvning af den resulterende graf, hvor farverne på H og y er de samme, er der ingen sekvens af farveudskiftninger på Kempe-kæder, der får farven på H til at afvige fra farven på y, siges den originale triangulering at være Kempe-låst med hensyn til kanten. Tilley beviste, at et minimum modeksempel til 4-farve sætningen skal være Kempe-låst med hensyn til hver eneste af dens kanter; hver kant i et minimum modeksempel skal have denne farveegenskab.

Kempe-låsning er en særlig restriktiv tilstand, der bliver vanskeligere at tilfredsstille, når en triangulering bliver større. Tilley satte sig for at finde ud af, om der er noget fælles for trianguleringer, der har Kempe-låste kanter. Hans tidligste søgning efter Kempe-låsning førte ham til Birkhoff-diamanten.

Birkhoff-diamanten
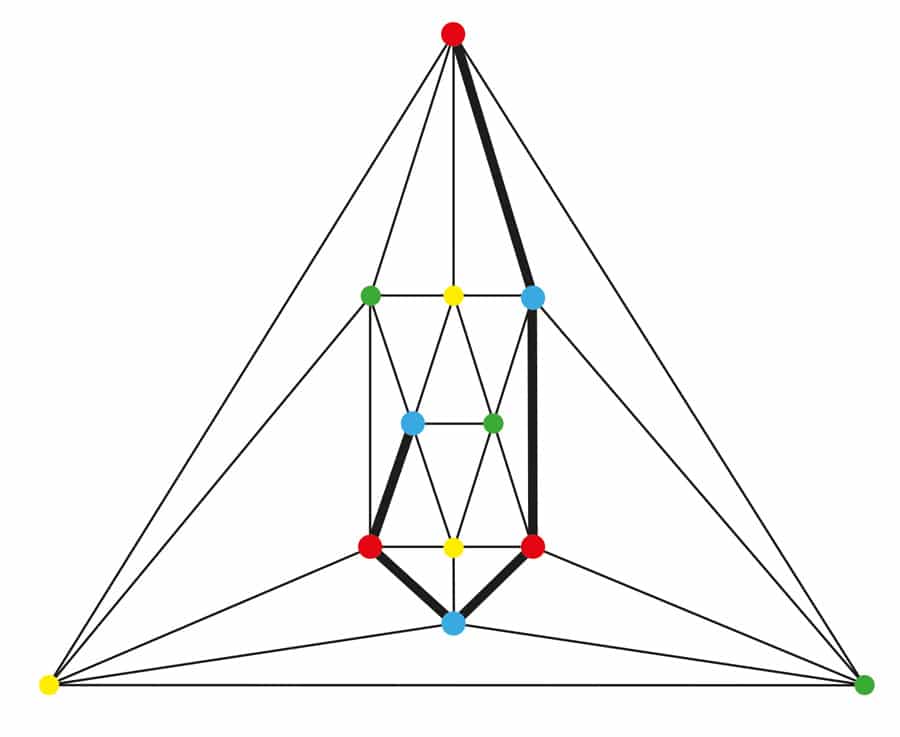
i 1913 opdagede G. D. Birkhoff, at en bestemt konfiguration af ti lande på et kort (en grænse ring af seks lande, der omslutter et sæt af fire lande) har en vigtig ejendom. Hvis denne konfiguration er til stede på et kort, og hvis underkortet med den fjernede konfiguration er 4-farvet, vil hele kortet være 4-farvet. Således kan et minimum modeksempel ikke indeholde den pågældende konfiguration. Det er blevet kendt som Birkhoff diamond. Tilley fandt ud af, at en Kempe-låst kant kun synes at opstå, når h og y også er slutpunkterne for grafversionen af en Birkhoff-diamant. Se Figur 2.

formodningen er let angivet, forståelig og spændende og giver en overbevisende forklaring på, hvorfor alle plane grafer er 4-farvede. da han ikke havde stødt på nogen Kempe-låsekonfiguration uden en Birkhoff-diamant, antog han, at Birkhoff-diamanten er den eneste ‘grundlæggende’ Kempe-låsekonfiguration, en der ikke indeholder en mindre Kempe-låsekonfiguration som en undergraf. Tilley fandt imidlertid, at han ikke kunne bevise sin kritiske formodning. Det var frustrerende, for hvis det var sandt, ville formodningen direkte bevise 4-farve sætningen. (For at være et minimum modeksempel skal en triangulering indeholde en Birkhoff diamond subgraph, men hvis det gjorde det, kunne det ikke være et minimum modeksempel.)

en overvældende understøttende sag
I stedet for at bevise sin formodning gjorde Tilley det næstbedste. Han besluttede at spille rollen som en eksperimentalist og opbygge en overvældende sag for at støtte hans formodning. Han delte alle relevante plane trianguleringer i to klasser: dem, hvor mindst fire hjørner skal fjernes, før graferne falder fra hinanden (4-tilsluttet), og dem, hvor mindst fem hjørner skal fjernes, før graferne falder fra hinanden (5-tilsluttet). Se Figur 3. Nyttigt i Tilleys omfattende søgning var, at han kun måtte undersøge et medlem af hver isomorfismeklasse (grafer, der er strukturelt identiske). Tilley undersøgte alle 8.044 isomorfisme klasser af 4-tilsluttede plane trianguleringer på op til 15 hjørner og alle 9.733 isomorfisme klasser af 5-tilsluttede plane trianguleringer på op til 24 hjørner. Han fandt kun tre Kempe-låste trianguleringer. Hver opdaget Kempe-låst kant indeholdt en Birkhoff-diamant, og hver forekom i en 4-forbundet triangulering. Der var slet ingen blandt 5-forbundne trianguleringer.

Tilley udvidede sin søgning blandt 4-forbundne trianguleringer ved at undersøge alle 30.926 isomorfismeklasser på 16 hjørner og alle 158.428 isomorfismeklasser på 17 hjørner. Beregningstidsbegrænsninger betød at begrænse hans søgning til prøver på 100.000 tilfældigt genererede ikke-isomorfe trianguleringer hver for klasser på 18,19 og 20 hjørner. Den udvidede søgning dukkede op 45 yderligere Kempe-låste trianguleringer, men nøjagtigt de samme resultater som den oprindelige søgning: hver Kempe-låst kant i en triangulering indeholdt en tilknyttet Birkhoff-diamant.

hvor herfra? Tilleys omfattende søgninger bekræftede let, at Birkhoff-diamanten er en grundlæggende Kempe-låsekonfiguration. Han har grundigt testet sin formodning, men det forbliver uprøvet. Hvis (eller hvornår) Tilleys formodning er bevist sand, dvs.at Birkhoff-diamanten alene er nøglen til 4 – farvelighed, ville det være en forbløffende forenkling af problemet: en enkelt konfiguration, der forklarer det hele-matematisk elegance.

bevis for 4-farve formodninger krævede indsatsen fra mange fremtrædende matematikere. Tilleys formodning om, at Birkhoff-diamanten er den eneste grundlæggende Kempe-låsekonfiguration, kan være endnu vanskeligere at bevise. De eksperimentelle beviser er dog stærke. Teoretikere kan sige ‘ hvorfor gider?’Tilleys svar er, at umættelig nysgerrighed vil vinde ud: “trods alt er formodningen let angivet, forståelig og spændende og giver en overbevisende forklaring på, hvorfor alle plane grafer er 4-farvede.”