Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
introduktion
firkantede rødder skrives oftest ved hjælp af et radikalt tegn, som dette,![]() . Men der er en anden måde at repræsentere at tage en rod på. Du kan bruge rationelle eksponenter i stedet for en radikal. En rationel eksponent er en eksponent, der er en brøkdel. For eksempel
. Men der er en anden måde at repræsentere at tage en rod på. Du kan bruge rationelle eksponenter i stedet for en radikal. En rationel eksponent er en eksponent, der er en brøkdel. For eksempel ![]() kan skrives som
kan skrives som ![]() .
.
kan du ikke forestille dig at hæve et tal til en rationel eksponent? De kan være svære at vænne sig til, men rationelle eksponenter kan faktisk hjælpe med at forenkle nogle problemer. Lad os undersøge forholdet mellem rationelle (fraktionerede) eksponenter og radikaler.
omskrivning af radikale udtryk ved hjælp af rationelle eksponenter
radikaler og fraktionerede eksponenter er alternative måder at udtrykke det samme på. Du har allerede set, hvordan firkantede rødder kan udtrykkes som en eksponent for halvdelen.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Husk, at kubering af et tal hæver det til kraften på tre. Bemærk, at i disse eksempler er nævneren for den rationelle eksponent tallet 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and rationelle eksponenter: nemlig at den nte rod af et tal kan skrives som enten ![]() eller
eller ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an udtryk indeholdende en rationel eksponent, du kan omskrive den ved hjælp af en radikal. I tabellen ovenfor skal du bemærke, hvordan nævneren for den rationelle eksponent bestemmer rodindekset. Så en eksponent for ![]() oversætter til kvadratroden, en eksponent for
oversætter til kvadratroden, en eksponent for ![]() oversætter til den femte rod eller
oversætter til den femte rod eller ![]() og
og ![]() oversætter til den ottende rod eller
oversætter til den ottende rod eller ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
Omskriv udtrykket med den fraktionerede eksponent som en radikal. Nævneren af fraktionen bestemmer roden, i dette tilfælde kubens rod. parenteserne i |
|
|
svar |
|
|
husk, at eksponenter kun henviser til mængden straks til deres venstre, medmindre der bruges et grupperingssymbol. Eksemplet nedenfor ligner meget det foregående eksempel med en vigtig forskel—der er ingen parenteser! Se hvad der sker.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Nævneren af fraktionen bestemmer roden, i dette tilfælde kubens rod. eksponenten refererer kun til den del af udtrykket umiddelbart til venstre for eksponenten, i dette tilfælde, men ikke 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. I dette tilfælde er indekset for radikalen 3, så den rationelle eksponent vil være DA 4 er uden for radikalet, er det ikke inkluderet i grupperingssymbolet, og eksponenten henviser ikke til det. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
svar |
|
|
rationelle eksponenter med andre tællere end en
alle tællerne for de fraktionerede eksponenter i eksemplerne ovenfor var 1. Du kan bruge fraktionerede eksponenter, der har andre tællere end 1 til at udtrykke rødder, som vist nedenfor. Bemærk nogen mønstre i denne tabel?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
for at omskrive en radikal ved hjælp af en fraktioneret eksponent bliver den kraft, som radikanten hæves til, tælleren, og roden bliver nævneren.
skrivning fraktionelle eksponenter
enhver radikal i formularen![]() kan skrives ved hjælp af en fraktioneret eksponent i formularen
kan skrives ved hjælp af en fraktioneret eksponent i formularen![]() .
.
forholdet mellem![]() og
og![]() arbejder for rationelle eksponenter, der også har en tæller på 1. For eksempel kan den radikale
arbejder for rationelle eksponenter, der også har en tæller på 1. For eksempel kan den radikale ![]() også skrives som
også skrives som ![]() , da ethvert tal forbliver den samme værdi, hvis det hæves til den første effekt. Du kan nu se, hvor tælleren på 1 kommer fra i den tilsvarende form af
, da ethvert tal forbliver den samme værdi, hvis det hæves til den første effekt. Du kan nu se, hvor tælleren på 1 kommer fra i den tilsvarende form af ![]() .
.
forenkling af radikale udtryk ved hjælp af rationelle Eksponenter og Eksponenternes Love
lad os udforske nogle radikale udtryk nu og se, hvordan man forenkler dem. Her er et radikalt udtryk, der skal forenkles, ![]() .
.
en metode til at forenkle dette udtryk er at faktorere og trække grupper af a3 ud, som vist nedenfor i dette eksempel.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
svar |
|
|
Du kan også forenkle dette udtryk ved at tænke på det radikale som et udtryk med en rationel eksponent og bruge princippet om, at enhver radikal i formularen ![]() kan skrives ved hjælp af en fraktioneret eksponent i formularen
kan skrives ved hjælp af en fraktioneret eksponent i formularen ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
begge forenklingsmetoder gav det samme resultat, a2. Afhængigt af problemets sammenhæng kan det være lettere at bruge den ene eller den anden metode, men for nu vil du bemærke, at du var i stand til at forenkle dette udtryk hurtigere ved hjælp af rationelle eksponenter end ved brug af “pull-out” – metoden.
lad os prøve et andet eksempel.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the rationel eksponent tilbage til radikal form. |
|
|
svar |
|
|
igen er den alternative metode at arbejde på at forenkle under radikalen ved hjælp af factoring. For det eksempel, du lige har løst, ser det sådan ud.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
lad os prøve et mere kompliceret udtryk, ![]() . Dette udtryk har to variabler, en brøkdel og en radikal. Lad os tage det trin for trin og se, om brug af fraktionerede eksponenter kan hjælpe os med at forenkle det.
. Dette udtryk har to variabler, en brøkdel og en radikal. Lad os tage det trin for trin og se, om brug af fraktionerede eksponenter kan hjælpe os med at forenkle det.
lad os starte med at forenkle nævneren, da det er her Det Radikale tegn er placeret.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Efter konvention betragtes et udtryk normalt ikke som forenklet, hvis det har en fraktioneret eksponent eller en radikal i nævneren. |
||
|
svar |
|
||
Nå, det tog et stykke tid, men du gjorde det. Du anvendte det, du ved om fraktionerede eksponenter, negative eksponenter og reglerne for eksponenter for at forenkle udtrykket.
Resume
en radikal kan udtrykkes som et udtryk med en fraktioneret eksponent ved at følge konventionen![]() . Omskrivning af radikaler ved hjælp af fraktionerede eksponenter kan være nyttigt til at forenkle nogle radikale udtryk. Når du arbejder med fraktionerede eksponenter, skal du huske, at fraktionerede eksponenter er underlagt alle de samme regler som andre eksponenter, når de vises i algebraiske udtryk.
. Omskrivning af radikaler ved hjælp af fraktionerede eksponenter kan være nyttigt til at forenkle nogle radikale udtryk. Når du arbejder med fraktionerede eksponenter, skal du huske, at fraktionerede eksponenter er underlagt alle de samme regler som andre eksponenter, når de vises i algebraiske udtryk.
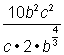
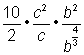
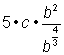
Leave a Reply