Articles

nemme permutationer og kombinationer

by admin

jeg har altid forvirret “permutation” og “kombination” — hvilken er hvilken?

Her er en nem måde at huske: permutation lyder kompliceret, ikke? Og det er det. Med permutationer betyder hver lille detalje noget. Alice, Bob og Charlie er forskellige fra Charlie, Bob og Alice (Indsæt dine venners navne her).

kombinationer er på den anden side ret nemme at gå. Detaljerne betyder ikke noget. Alice, Bob og Charlie er de samme som Charlie, Bob og Alice.

permutationer er for lister (rækkefølge betyder noget) og kombinationer er for grupper (rækkefølge betyder ikke noget).

Du ved, en “kombinationslås” skal virkelig kaldes en “permutationslås”. Ordren du sætter tallene i sager.

lette permutationer og kombinationer

en ægte “kombinationslås” ville acceptere både 10-17-23 og 23-17-10 som korrekt.

permutationer: de hårede detaljer

lad os starte med permutationer eller alle mulige måder at gøre noget på. Vi bruger fancy-pants udtrykket” permutation”, så vi vil bekymre os om hver eneste detalje, herunder rækkefølgen af hver vare. Lad os sige, at vi har 8 personer: 

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

hvor mange måder kan vi tildele en 1., 2. og 3. plads præmie blandt otte deltagere? (Guld / sølv / Bronse)

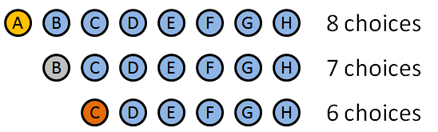
permuationseksempelmedaljer

Vi skal bruge permutationer, da den rækkefølge, vi uddeler disse medaljer, betyder noget. Sådan bryder det ned:

  • guldmedalje: 8 valg: A B C D E F G H (Smart hvordan jeg fik navnene til at matche bogstaver, eh?). Lad os sige en vinder guldet.
  • sølvmedalje: 7 valg: B C D E F G H. lad os sige, at B vinder Sølvet.
  • bronsmedalje: 6 valg: C D E F G H. lad os sige… C vinder bronsen.

Vi valgte visse mennesker til at vinde, men detaljerne betyder ikke noget: vi havde 8 valg først, derefter 7, derefter 6. Det samlede antal muligheder var $8 * 7 * 6 = 336$.

lad os se på detaljerne. Vi var nødt til at bestille 3 personer ud af 8. For at gøre dette startede vi med alle muligheder (8) og tog dem derefter væk en ad gangen (7, derefter 6), indtil vi løb tør for medaljer.

Vi ved, at faktoren er:

\displaystyle{ 8! = 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \cdot 3 \ cdot 2 \ cdot 1 }

desværre gør det for meget! Vi vil kun have $8 * 7 * 6$. Hvordan kan vi” stoppe ” faktorialet ved 5?

det er her permutationer bliver seje: bemærk, hvordan vi vil slippe af med $5 * 4 * 3 * 2 * 1$. Hvad er et andet navn til dette? 5 factorial!

så hvis vi gør 8!/5! vi får:

\displaystyle {\frac{8!}{5!} = \frac{8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \cdot 3 \ cdot 2 \ cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \cdot 6}

og hvorfor brugte vi nummeret 5? Fordi det blev tilovers efter vi plukket 3 medaljer fra 8. Så en bedre måde at skrive dette på ville være:

\displaystyle{\frac{8!}{(8-3)!}}

hvor 8!/(8-3)! er bare en fancy måde at sige “Brug den første 3 numre af 8!”. Hvis vi har n elementer i alt og ønsker at vælge k i en bestemt rækkefølge, får vi:

\displaystyle{\frac{n!} {(n-k)!}}

og dette er den smarte permutationsformel: du har n-varer og vil finde antallet af måder,k-varer kan bestilles på:

\displaystyle{P(n, k) = \frac{n!} {(n-k)!}}

kombinationer, Ho!

kombinationer er nemme at gå. Orden betyder ikke noget. Du kan blande det op, og det ser det samme ud. Lad os sige, at jeg er en cheapskate og ikke har råd til separate guld -, sølv-og Bronsmedaljer. Faktisk har jeg kun råd til tomme dåser.

hvor mange måder kan jeg give 3 dåser til 8 personer?

Nå, i dette tilfælde betyder den rækkefølge, vi vælger folk, ikke noget. Hvis jeg giver en dåse til Alice, Bob og derefter Charlie, er det det samme som at give til Charlie, Alice og derefter Bob. På den ene eller anden måde, de er lige så skuffede.

dette rejser et interessant punkt-vi har nogle afskedigelser her. Alice Bob Charlie = Charlie Bob Alice. Et øjeblik, lad os bare finde ud af, hvor mange måder vi kan omarrangere 3 personer.

Nå, vi har 3 Valg for den første person, 2 for den anden og kun 1 for den sidste. Så vi har $3 * 2 * 1$ måder at omarrangere 3 personer.

vent et øjeblik … dette ser lidt ud som en permutation! Du narrede mig!

det gjorde jeg faktisk. Hvis du har n mennesker, og du vil vide, hvor mange arrangementer der er for dem alle, er det bare N factorial eller N!

så hvis vi har 3 dåser at give væk, er der 3! eller 6 variationer for hvert valg, vi vælger. Hvis vi vil finde ud af, hvor mange kombinationer vi har, skaber vi bare alle permutationer og deler med alle afskedigelser. I vores tilfælde får vi 336 permutationer (ovenfra), og vi deler med de 6 afskedigelser for hver permutation og får 336/6 = 56.

den generelle formel er

\displaystyle{C(n,k) = \frac{P (n,k)}{k!}}

hvilket betyder ” Find alle måder at vælge k folk fra n, og divider med k! variant”. Når vi skriver dette ud, får vi vores kombinationsformel eller antallet af måder at kombinere k-elementer fra et sæt n:

\displaystyle{C(n,k) = \frac{n!} {(n-k)!k!}}

Nogle gange er C(n,k) skrevet som:

\displaystyle{\binom {n}{k}}

som er binomialkoefficienten.

et par eksempler

Her er et par eksempler på kombinationer (rækkefølge betyder ikke noget) fra permutationer (ordre betyder noget).

  • kombination: Vælg et hold på 3 personer fra en gruppe på 10. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    Permutation: vælg en præsident, VP og Vanddreng fra en gruppe på 10. $P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • kombination: valg af 3 desserter fra en menu på 10. C (10,3) = 120.

    Permutation: notering dine 3 foretrukne desserter, i rækkefølge, fra en menu på 10. P (10,3) = 720.

husk ikke formlerne, forstå hvorfor de virker. Kombinationer lyder enklere end permutationer, og de er. Du har færre kombinationer end permutationer.

andre indlæg i denne serie

  1. nemme permutationer og kombinationer
  2. Naviger et gitter ved hjælp af kombinationer og permutationer
  3. sådan forstår du kombinationer ved hjælp af multiplikation
  4. hvorfor multiplicerer vi kombinationer?