grafen for en lineær ulighed i en variabel er en talelinje. Brug en åben cirkel til < og > og en lukket cirkel for prit og prit.

grafen for> -3

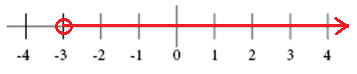
grafen for 2

den samme løsning kaldes ækvivalent. Der er egenskaber ved uligheder såvel som der var egenskaber ved lighed. Alle nedenstående egenskaber gælder også for uligheder, der involverer kr.og kr.

tilføjelsesegenskaben for ulighed siger, at tilføjelse af det samme tal til hver side af uligheden producerer en tilsvarende ulighed

$$if\:>y,\: derefter\:>y+å$$

$$If\:<y,\: derefter\:< y+å$$

subtraktionsegenskaben for ulighed fortæller os, at at trække det samme tal fra begge sider af en ulighed giver en tilsvarende ulighed.

$$If\:>y,\: derefter\:s>y-$$

$$If\:<y,\: derefter\: S-s<y-å$$

multiplikationsegenskaben for ulighed fortæller os, at multiplikation på begge sider af en ulighed med et positivt tal producerer en tilsvarende ulighed.

$ $ If \:>y \: og\: >0,\: derefter\:>y$$

$$If\: <y\: OG\: Å>0,\: derefter\:<y$$

multiplikation i hver side af en ulighed med et negativt tal på den anden side producerer ikke en tilsvarende ulighed, medmindre vi også vender retningen af Ulighedssymbolet

$$if\: >y \: OG\: Å<0,\: derefter\:<$$

$$if\: <Y\: og\: s <0,\: derefter\: s> s$$

det samme gælder for divisionens egenskab af ulighed.

opdeling af begge sider af en ulighed med et positivt tal giver en tilsvarende ulighed.

$$If\:>y \: OG\: Å>0,\: derefter\: \frac {} {å}>\frac{y}{å}$$

$$If\:<y\: OG\: Å>0,\: derefter\:<\frac{y}{å}$$

og opdeling på begge sider af en ulighed med et negativt tal giver en tilsvarende ulighed, hvis ulighedssymbolet vendes.

$$If\:>y \: OG\: Å<0,\: derefter\: \frac {} {å}<\frac{y}{å}$$

$$If\:<y\: OG\: Å<0,\: derefter\: \frac {{å}>\frac{y} {å}$$

for at løse en ulighed i flere trin gør du som du gjorde, da du løste multi-trins ligninger. Tag en ting på det tidspunkt, helst ved at isolere variablen fra konstanterne. Når man løser uligheder i flere trin, er det vigtigt ikke at glemme at vende ulighedstegnet, når man multiplicerer eller deler med negative tal.

eksempel

Løs uligheden

$$-2\venstre ( 3 \højre) < 10$$