komplekse tal: introduktion (side 1 af 3)

sektioner: introduktion, operationer med komplekser, den kvadratiske formel

indtil nu har du fået at vide, at du ikke kan tage kvadratroden af et negativt tal. Det skyldes, at du ikke havde nogen tal, der var negative, efter at du havde kvadreret dem (så du kunne ikke “gå baglæns” ved at tage kvadratroden). Hvert tal var positivt, efter du kvadrerede det. Så du kunne ikke meget godt kvadratrod en negativ og forventer at komme op med noget fornuftigt.

nu Kan du dog tage kvadratroden af et negativt tal, men det indebærer at bruge et nyt tal til at gøre det. Dette nye nummer blev opfundet(opdaget ?) omkring Reformationens tid. På det tidspunkt troede ingen, at der ville blive fundet nogen “reel verden” til dette nye nummer, bortset fra at lette de beregninger, der var involveret i løsning af visse ligninger, så det nye nummer blev betragtet som et foregive nummer opfundet for nemheds skyld.

(men så, når du tænker over det, er ikke alle numre opfindelser? Det er ikke som tal vokser på træer! De lever i vores hoveder. Vi lavede dem alle sammen! Hvorfor ikke opfinde en ny, så længe det fungerer okay med det, vi allerede har?)

derefter:

nu tror du måske, at du kan gøre dette:

men det giver ingen mening! Du har allerede to tal, der kvadrerer til 1; nemlig -1 og +1. Og jeg har allerede kvadrater til -1. Så det er ikke rimeligt, at jeg også vil kvadrere til 1. Dette påpeger en vigtig detalje: Når du beskæftiger dig med fantasi, får du noget (evnen til at håndtere negativer inde i firkantede rødder), men du mister også noget (nogle af de fleksibilitet og praktiske regler, du plejede at have, når du beskæftiger dig med firkantede rødder). Især skal du altid gøre i-delen først!

• forenkling af KVRT(-9). Copyright 2000-2011 Alle rettigheder forbeholdes

(advarsel: det trin, der går gennem det tredje “lig” – tegn, er ” “, ikke ““. Jeg er uden for det radikale.)

• forenkle KVRT (-25).

• Simplificer KVRT(-18).

• Simplify(-6).

i dine beregninger, vil du beskæftige sig med jeg lige som du ville med H, bortset fra det faktum, at H2 er bare H2, men i2 er -1:

• forenkle 2i + 3i.

2i + 3i = (2 + 3)i = 5I

• forenkle 16I – 5i.

16i – 5i = (16 – 5)i = 11i

• multiplicere og forenkle (3i)(4i).

(3i) (4i) = (3 * 4) (i·i) = (12) (i2) = (12)(-1) = -12

• Multiplicer og simplificer (i)(2i)(–3i).

(i) (2i) (–3i) = (2 · -3) (i · i · i) = (-6) (i2 · i)

=(-6) (-1 · i) = (-6) (–i) = 6i

Bemærk Dette sidste problem. Inden for det kan du se, at , fordi i2 = -1. Fortsætter, vi får:

dette mønster af kræfter, Tegn, 1 ‘er og jeg’ er er en cyklus:

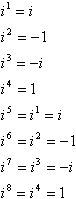
med andre ord, for at beregne enhver høj effekt af i, kan du konvertere den til en lavere effekt ved at tage det nærmeste multiplum af 4, der ikke er større end eksponenten og trække dette multiplum fra eksponenten. For eksempel er et almindeligt trickspørgsmål ved test noget i retning af “forenkle i99”, ideen er, at du vil prøve at formere mig nioghalvfems gange, og du løber tør for tid, og lærerne får en god fnise på din bekostning i fakultetsloungen. Her er hvordan genvejen fungerer:

i99 = i96+3 = i(4 lig 24)+3 = i3 = –i

det vil sige, i99 = i3, fordi du bare kan lop off i96. (Halvfems seks er et multiplum af fire, så i96 er kun 1, som du kan ignorere.) Med andre ord kan du dele eksponenten med 4 (ved hjælp af lang division), kassere svaret og kun bruge resten. Dette vil give dig den del af eksponenten, som du holder af. Her er et par flere eksempler:

• forenkle i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• forenkle i120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• forenkle i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>