Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
소개
스퀘어 뿌리는 가장 자주 사용하여 작성한 급진적인 기호,이 같은![]()
![]()
![]() 로 쓸 수 있습니다.
로 쓸 수 있습니다.
합리적인 지수로 숫자를 올리는 것을 상상할 수 없습니까? 그들은 익숙해지기가 어려울 지 모르지만 합리적인 지수는 실제로 몇 가지 문제를 단순화하는 데 도움이 될 수 있습니다. 합리적인(분수)지수와 급진주의 자 사이의 관계를 탐구합시다.
다시 쓰기가 급진적인 표현을 사용하여 합리적 지
활성 산소 분수 지수는 대체 방법으로 표현하는 동일한 것입니다. 당신은 이미 제곱근이 1/2 의 힘에 대한 지수로 표현 될 수있는 방법을 보았습니다.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. 기억하십시오,숫자를 새끼를 낳는 것은 그것을 3 의 힘으로 올립니다. 이 예에서 합리적인 지수의 분모는 숫자 3 임을 알 수 있습니다.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and 합리적인 지수:즉,n 번째 루트의 숫자 작성할 수 있습 중 하나로![]()
![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an 합리적인 지수를 포함하는 표현식,당신은 급진적 인 것을 사용하여 그것을 다시 쓸 수 있습니다. 위의 표에서 합리적인 지수의 분모가 루트의 지수를 결정하는 방법에 주목하십시오. 그래서 지수의![]()
![]()
![]() ,and
,and![]()
![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
다시 표현으로 분수수로 급진적으로 합니다. 분수의 분모는 루트,이 경우 큐브 루트를 결정합니다.
|
|
|
대답 |
|
|
기억하는 지수만 참조하면 수량이 바로 그들의 남지 않는 한 그룹을 상징이 사용됩니다. 아래 예제는 하나의 중요한 차이점이있는 이전 예제와 매우 흡사합니다-괄호가 없습니다! 무슨 일이 일어나는지보세요.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. 분수의 분모는 루트,이 경우 큐브 루트를 결정합니다. 지수는 지수의 바로 왼쪽에있는 표현식의 일부만을 나타내지 만,이 경우에는 x 이지만 2 는 아닙니다. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. 이 경우 라디칼의 지수는 3 이므로 합리적인 지수는 4 는 라디칼 외부에 있으므로 그룹화 기호에 포함되지 않으며 지수는이를 참조하지 않습니다. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
대답 |
|
|
합리적인 해설자와 분자가 다른 하나 이상
의 모든증 소수 지수 위의 예제에서 1. 아래 그림과 같이 1 이외의 분자가있는 분수 지수를 사용하여 뿌리를 표현할 수 있습니다. 이 테이블 내의 모든 패턴을 알 수 있습니까?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
을 다시 급진적인 사용하는 분수 지수, 전원하는 radicand 은 제기된 분자와 루가트립입니다.
쓰기 분수 지수
어떤 근본적인 형태에서![]()
![]() .
.
![]()
![]()
![]()
![]()
![]() 의 동등한 형태로 어디에서 왔는지 볼 수 있습니다.
의 동등한 형태로 어디에서 왔는지 볼 수 있습니다.
단순화 급진적인 표현을 사용하여 합리적인 지수 및 법률의 지수
항상 성실하게 수업을 진행하 급진적인 식 지금 및 단순화하는 방법을 참조하십시오니다. 다음은 단순화가 필요한 급진적 인 표현입니다.![]() .
.
이 표현을 단순화하는 한 가지 방법은이 예제에서 아래 그림과 같이 a3 그룹을 요인 화하고 끌어내는 것입니다.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
대답 |
|
|
단순화할 수도 있습니다 이런 표현에 대해 생각하여 급진적인 표현으로 합리적 지수 및 원리를 이용하여는 근본적인 형태에서![]()
![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
두 단순화 방법 모두 동일한 결과를 얻었습니다. 의 컨텍스트에 따라 문제가 될 수 있게 한 가지 방법을 사용하거나,다른 하지만 지금은,당신은 당신이었을 간소화할 수 있는 이 식 더 빠르게 사용하는 합리적인 지수 이상을 사용할 때는”철”방법입니다.
다른 예를 시도해 보겠습니다.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the 급진적 인 형태로 다시 합리적인 지수. |
|
|
대답 |
|
|
다시 다른 방법은 작업을 간소화하는 데에 급진적 인 사용하여 고려해. 방금 해결 한 예제의 경우 다음과 같습니다.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A)![]()
B)![]()
C)![]()
D) ![]()
시도하자는 더 복잡한 식![]() . 이 표현식에는 분수 와 급진적 인 두 가지 변수가 있습니다. 단계별로 살펴보고 분수 지수를 사용하여 단순화하는 데 도움이되는지 살펴 보겠습니다.이것이 급진적 인 기호가있는 곳이기 때문에 분모를 단순화하는 것으로 시작합시다.
. 이 표현식에는 분수 와 급진적 인 두 가지 변수가 있습니다. 단계별로 살펴보고 분수 지수를 사용하여 단순화하는 데 도움이되는지 살펴 보겠습니다.이것이 급진적 인 기호가있는 곳이기 때문에 분모를 단순화하는 것으로 시작합시다.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. 규칙에 따라 표현식은 분모에 분수 지수 또는 급진파가있는 경우 일반적으로 단순화 된 것으로 간주되지 않습니다. |
||
|
대답 |
|
||
론,는 동안,하지만 당신은 그것을 했다. 분수 지수,음수 지수 및 지수의 규칙에 대해 알고있는 것을 적용하여 표현을 단순화했습니다.
요약
급진적으로 표현할 수 있다는 표현으로 분수수에 의해 다음 규칙![]() . 분수 지수를 사용하여 라디칼을 다시 작성하는 것은 일부 급진적 인 표현을 단순화하는 데 유용 할 수 있습니다. 작업을 할 때는 분수는 지를 기억하는 분수 지수는 동일한 규칙의 모든 다른 지수는 나타날 때는 주로 가환 혹은 비가환 유체 표현입니다.
. 분수 지수를 사용하여 라디칼을 다시 작성하는 것은 일부 급진적 인 표현을 단순화하는 데 유용 할 수 있습니다. 작업을 할 때는 분수는 지를 기억하는 분수 지수는 동일한 규칙의 모든 다른 지수는 나타날 때는 주로 가환 혹은 비가환 유체 표현입니다.
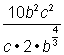
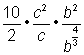
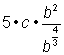
Leave a Reply