&Boxes5-수 SummaryIQRs&Outliers

왜 아웃 라이어에 대한 상자의 너비가 1.5 배입니까? 왜 그 특정 값이”허용 가능한”값과”받아 들일 수없는”값의 차이를 demark 합니까? 왜냐하면 John Tukey 가 1977 년에 box-and-whisker 플롯을 발명하여 이러한 값을 표시 할 때,그는 1.5×iqr 을 outliers 의 demarkation 라인으로 선택했기 때문입니다. 이것은 잘 작동 했으므로 그 이후로 그 가치를 계속 사용했습니다. 는 경우에 당신은 더 이상 갈 통계로,당신은 당신을 찾을 수 있는 측정의 합리성,대 벨 곡선 모양의 데이터,의미 있는 일반적으로만 만큼 어쩌면 중 하나에 대해 퍼센트 데이터의 것이 특이하다.

사용할 수 있습니다 스냅 위젯은 아래 연습을 찾는 Interquartile 범위,또한”H-퍼짐”(또는 건너 뛰고 계속 수업). 입력 한 운동을 시도하거나 자신의 운동을 입력하십시오. 그런 다음 버튼을 클릭하고”쿼터 간 범위 찾기(H-스프레드)”로 아래로 스크롤하여 Mathway 의 답을 비교하십시오.

(유료 업그레이드를 위해 Mathway 사이트로 직접 이동하려면”단계를 보려면 탭”을 클릭하십시오.)

10.2,14.1,14.4. 14.4, 14.4, 14.5, 14.5, 14.6, 14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4

아웃 라이어가 있는지 알아 보려면 먼저 IQR 을 찾아야합니다. 15 개의 데이터 포인트가 있으므로 중앙값은 8 번째 위치에있게됩니다.

그런 다음 Q2=14.6.

중앙값의 양쪽에 7 개의 데이터 포인트가 있습니다. 두 반쪽은 다음과 같습니다.

값 Q1–1.5×IQR 및 Q3+1 입니다.5×IQR 은 이상치 값에서”합리적인”값을 표시하는”울타리”입니다. 아웃 라이어는 울타리 밖에 놓여 있습니다.

경우에 당신의 배정을 고려할 뿐만 아니라 특이한”극단적인 값을”다음에 대한 값 Q1–1.5×IQR 및 Q3+1.5×IQR 은”안”울타리와 값을 Q1–3×IQR 및 Q3+3×IQR 는”외”담.

특이(별표로 표시 또는 열 점)사이의 내부 및 외부의 울타리,그리고 극단적인 값(표시가 어느 상징을 사용하지 않았을 위한 이상값)외부에 있는 외부의 울타리.

그런데,당신의 책은”1.5×IQR”의 값을”단계”로 나타낼 수 있습니다. 그 특이 될 것입니다 숫자를 하나 사이에 두 단계에서 경첩,그리고 극단적인 값을 것이 숫자는 더 이상 두 단계에서 경첩.

고 다시 이전를 들어,외 담 것에 14.4–3×0.5=12.9 및 14.9+3×0.5=16.4. 16.4 가 위쪽 바깥 쪽 울타리에 바로 있기 때문에 이것은 극단적 인 값이 아닌 이상치로만 간주 될 것입니다. 그러나 10.2 는 더 낮은 외부 울타리 아래에 완전히 있으므로 10.2 는 극단적 인 값이됩니다.

귀하의 계산기지 않을 수 있는지 여부를 나타냅자-플롯을 포함 특이하다. 예를 들어,위의 문제는 점 10.2,15.9 및 16.4 를 이상 치로 포함합니다. 중 하나에 설정 나의 계산기게 간단하자-플롯을 사용하는 다섯 번호 요약,그래서 더 이상값은 다음과 같으로 끝점의 수:

는 다른 계산기 설정을 제공자-플롯으로 이상값이 특별히 표시(이 경우,의 시뮬레이션으로 오픈 dot),그리고 수염을 것만으로 가장하고 가장 낮은 값이 없는 이상값:

나의 계산기지 구분할 수 없는 이상값이고 극단적인 값입니다. 당신도 그렇지 않을 수도 있습니다. 다음 테스트 전에 소유자 설명서를 지금 확인하십시오.

를 사용하는 경우 귀하의 선에 도움이 이러한 플롯을 알고 있는지 확인하는 설정되어 있어를 사용하여 어떤 결과가 의미하거나,계산을 제공 할 수 있습이 완벽하게 올바르지만”잘못된”대답합니다.

• 다음 데이터 세트에 대해 이상치 및 극단 값(있는 경우)을 찾아 상자 및 위스커 플롯을 그립니다. 별표가있는 이상치 및 열린 점이있는 극단적 인 값을 표시하십시오.

광고

을 찾기 위해 특이하고 극단적인 값을 나는 먼저 찾 IQR. 이 있기 때문에 일곱 목록에 있는 값,중간값은 네 번째 값:

Q2=25

전반의 목록입니다:

21,23,24

…그래서 Q1=23 일;하반기:

29 일 33,49

…그래서 Q3=33. 그런 다음 IQR 은 다음에 의해 제공됩니다:

IQR=33–23=10

특이 될 것입니다 어떤 아래의 값:

23 – 1.5×10 = 23 – 15 = 8

…또는 위

33 + 1.5×10 = 33 + 15 = 48

극단적인 값을 것입니다 그래

23 – 3×10 = 23 – 30 = -7

…또는 위

33 + 3×10 = 33 + 30 = 63

그래서 나는 국외에서 49 그러나 없이 극단적인 값입니다. Q3 도 가장 높은 비 이상치이기 때문에 내 음모에 최고 수염을 갖지 않을 것입니다. 그래서 내 음모는 다음과 같습니다:

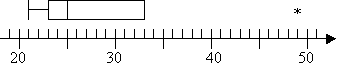
주목해야한다는 방법들을 통해,규정 및 규칙 위에서 설명하는 내가 무엇을 가르치고 내가 본 가장 일반적으로 가르쳤다. 그러나 코스에 특정 규칙이 다를 수도 있고 계산기가 계산을 약간 다르게 수행 할 수도 있습니다. 교과 과정에 특정한 답을 찾는 데 다소 유연해야 할 수도 있습니다.나는 이것이 내가 할 수있는 일이 아니라는 것을 알고 있지만,내가 할 수있는 일은 내가 할 수있는 일이 아니라는 것이다.