beanz 잡지
여지도를 혼-Erben(1652)Wikipedia
이달의 수학 퍼즐을 다시 날짜 1735 되었을 때 첫 번째에 의해 해결 레온하르트 성당,오일러,스위스 수학자 및 물리학입니다.
퍼즐은 쾨니히 스 베르크의 일곱 다리라고합니다. 실제 도시를 기반으로 한 다음 프로이센에,지금은 러시아의 칼리닌그라드에 있습니다. 도시는 사이에 두 개의 섬이있는 강으로 나뉘며,더 하류로,강은 도시를 다시 나눕니다.문제는 믿을 수 없을 정도로 간단합니다.: 두 섬과 마을의 하류 부분을 연결하는 일곱 다리가있다(또는 오일러의 시간에 있었다). 오일러는지 궁금하면 사람이 할 수 있는 걸쳐 각각의 일곱 교량 한 번만 모든 부분의 도시입니다. 같은 자리에서 시작하고 끝내는 것은 요구 사항이 아니 었습니다.
여기에도 사용할 수 있는 시도하고 문제를 해결하기 위해 자신을 위해:
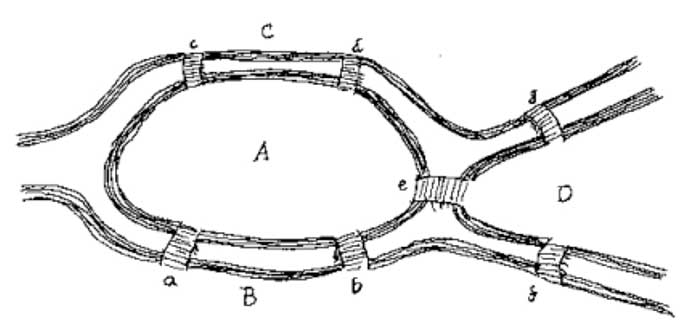
는 당신이 생각하는 것은 더 중요한 것이 문제를 해결하기: 교량의 수 또는 각 교량의 위치?
대답:교량의 수.
오일러 증명 수리해야 합 짝수,예를 들어,여섯 개의 교량신의 일곱,당신이 산책하고 싶은 경우에는 각 다리를 한번에 여행의 각 부분에 쾨니히 스 베르크. 솔루션은 각 브리지를 끝점,수학적 용어의 정점 및 각 브리지(정점)간의 연결로 봅니다. 오일러를 실현하의 짝수 교량 산출 정확한 결과할 수 있는 터치의 모든 부분을 마지 않고 다리를 건너다.
오일러 사용되는 수학은 그것을 증명하는 불가능했을 십자가에 모든 세븐 브리지만 한 번 방문의 모든 부분에 쾨니히 스 베르크. 이렇게 함으로써,그 모션에서 설정 시리즈의 발견 그리고 통찰력에 대해 어떻게 공간을 교차하는 공간을 정의할 수 있습뿐만 아니라,자신의 속성입니다. 오일러의 솔루션에 대한 자세한 설명은이 기사 아래의 위키 백과 링크에서.예를 들어 뫼비우스 스트립을 본 적이 있다면 오일러의 해결책에서이 문제로 진화 한 수학적 연구 분야 인 토폴로지의 예를 보았습니다. 토폴로지는 공간의 연속성과 경계뿐만 아니라 공간과 사물이 서로 어떻게 연결되는지에 관한 것입니다. 토폴로지는 또한 공간이 확장되거나 계약 될 때 공간의 속성이 변경되고 변경되지 않는 방법을 연구합니다.
에 컴퓨팅,토폴로지를 이해하는데 유용 네트워크(경로)할 수 있는 데이터 흐름을 내에서 어떤 시스템뿐만 아니라,어떻게 데이터 세트와 관련이 있을 수 있습니다. 일곱이 브리지의 쾨니히 스 베르크도 유사한 또 다른 일반적인 컴퓨팅 문제라고 때로는 외판원 문제가 당신을 찾으려고 가장 효율적인 경로를 주의 제한과 같은 일곱이 브리지에서 오일러의 문제입니다.
비 수학자(아마도 당신,확실히 나)는 우리가 기차 나 버스를 타면 언제든지 여행 세일즈맨 문제를 경험합니다. 여행 세일즈맨 문제는 지정된 거리의 도시 쌍 사이를 여행하는 가장 효율적인 방법을 알아내는 것입니다. 관리 부족한 자원(기차,버스)는 여행에 따라 유한 경로 완벽한 문제에 대한 컴퓨팅를 해결하기 때문에 컴퓨터가 더 빠르고 효율적입니다. 그러나 먼저 문제를 진술하고 수학으로 해결책을 정의하기 위해 오일러와 다른 사람들이 필요합니다. 우리는 그 때 수학을 하기 위하여 우리의 컴퓨터를 프로그램한다.
토폴로지역을 설정 이론,방법 그룹의 것을 정렬할 수 있습으로 세트를 식별하는 일반적인 요소뿐만 아니라 다른 그룹으로 독특한 요소입니다. 벤 다이어그램은 세트의 좋은 예입니다. 그리고 프로그래밍은 때로는 다른 방식으로 데이터를 정렬해야합니다. 어떤 정렬 방법이 상황에 가장 적합한 지 설정 이론에 의해 결정될 수 있습니다.
그리고 오일러 시대의 일곱 다리는 어떻게 되었습니까? 두 사람은 2 차 세계 대전에서 살아남지 못했습니다.두 다리는 철거되어 단일 고속도로로 교체되었습니다. 의 나머지 세 다리,하이에 재건되었 1935 년 동안 다른 두 남아 있는 그대로 오일러 그들을 알았다. 그리고 물론,Königsberg,프로이센은 칼리닌그라드,러시아에 이름을 변경했습니다.
Leave a Reply