피보나치 시퀀스
피보나치 시퀀스는 일련의 숫자입니다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
다음의 번호가 있을 추가하여 두 번호하기 전에 그것
- 2 찾을 추가하여 두 번호하기 전에 그것(1+1),
- 3 찾을 추가하여 두 번호하기 전에 그것(1+2),
- 5(2+3),
- 에!
예:위의 시퀀스의 다음 숫자는 21+34=55
그렇게 간단합니다!
여기에 더 긴 목록이 있습니다:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …다음 몇 개의 숫자를 알아낼 수 있습니까?
만드는 나선형
때 우리는 사각형으로 이러한 폭로,우리는 좋은 나선형
어떻게 볼 수 있는 광장에 맞는 깔끔하게 함께?
예를 들어 5 와 8 은 13 을,8 과 13 은 21 을,등등.

이 나선은 자연에서 발견됩니다!
참조: 자연,황금 비율,그리고 피보나치
규칙
피보나치 순서를 작성할 수 있습으로”규칙”(사).
먼저,용어는 다음과 같이 0 부터 번호가 매겨집니다:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
따라서 용어 번호 6 은 x6(8 과 같음)이라고합니다.
|
예:8 기 x8=x7+x6 |
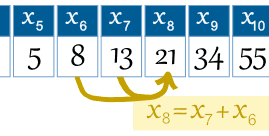 |
그래서 우리는 쓸 수 있는 규칙
이 규칙은 xn=xn−1+xn−2
가:
- xn 은 용어는 번호”n”
- xn−1 은 이전 기간(n−1)
- xn−2 은 용어는 그 전에(n−2)
예:용어 9 은 다음과 같이 계산됩니다:
황금 비율
여기에는 놀라운 것입니다. 우리가 어떤 두 개의 연속도(다)피보나치 숫자,그들의 비율은 매우 가까운 골든 비율의”φ”약 1.618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…나는 이것이 내가 할 수있는 유일한 방법이라고 생각한다…
|
우리는 없을 시작으로 2,3,여기에 내가 무작위로 선택했 192 16(및 순서 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…나는 이것이 내가 할 수있는 유일한 방법이라고 생각한다…
|
그 이상을 얻을 좋은 가치 있지만,그것을 보여줍니다 그냥 피보나치 작업을 수행 할 수 있습니다!
황금 비율을 사용하여 피보나치 계산 숫자
도 더 놀라운 것은 우리가 계산할 수있는 모든 피보호를 사용하의 황금 비율:
xn=φn−(1−φ)n√5
응답이 제공으로 전체 수,정확히 동일한 이전의 두 가지 용어입니다.
예:x6
x6=(1.618034…)6 − (1−1.618034…의 경우)6√5
때 사용된 계산에 이(만 들어가 황금 비율을 6 개 소수 자릿수)나는 대답을 얻었 8.00000033,더 정확한 계산에 가까운 것입 8.
N=12 를 시도하고 당신이 얻는 것을 보아라.
를 계산할 수도 있습니한 피보나치 수을 곱하여 이전에 피보나치 숫자에 의하여 황금 비율과 그림(에 대한 작품 번호 위의 1):
예:8×φ=8×1.618034… = 12.94427… =13(반올림)
몇 가지 흥미로운 것들
여기에 피보나치 시퀀스가 다시 있습니다:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
흥미로운 패턴이 있습니다.
- 숫자 x3=2 를 살펴보십시오. 모든 3 번째 숫자는 다음과 같은 배수입니다 2 (2, 8, 34, 144, 610, …)
- 숫자 X4=3 을 살펴보십시오. 매 4 번째 숫자는 3 의 배수입니다(3,21,144,…)
- 숫자 X5=5 를 살펴보십시오. 모든 5 번째 숫자는 5 의 배수입니다(5,55,610,…)
등등(모든 n 번째 숫자는 xn 의 배수입니다).
1/89=0.011235955056179775…
주의 처음 몇 자리(0,1,1,2,3,5)는 피보나치 시퀀스입니까?다음과 같이 여러 자리 숫자(13,21 등)가 겹치는 것을 제외하고는 모두 다음과 같습니다.
.. 등…나는 이것이 어떻게 작동 하는지를 모른다… =1/89
용어는 영
순서 작품을 아래로 또한,다음과 같다:
| n= | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(을 증명하는 각각의 번호를 찾을 추가하여 두 번호하기 전에!)
사실 0 이하의 시퀀스는 a+-+-를 따르는 것을 제외하고는 0 위의 시퀀스와 동일한 숫자를 갖습니다… 패턴. 그것을 작성할 수 있습 like this:
x n=(-1)n+1xn
다고 말하는 용어”n”같(-1)n+1 시간 기간”n”,그리고 가치(-1)n+1 깔끔하게 만드는 올바른+1, -1, +1, -1, … 패턴.
역사
피보나치지 않을 알고 먼저 시퀀스에 대한 알려져 있었습니다 인도에서는 수백 년 전에!

에 대한 피보나치 남자
진짜 자신의 이름 레오나르도 피사노 Bogollo,그가 살았던 사 1170 및 1250 에서 이탈리아입니다.
“피보나치”는 대략”보나치의 아들”을 의미하는 그의 별명이었습니다.
뿐 아니라 유명한 피보나치,그가 전파되었 힌두교-아라비아 숫자(다음과 같이 우리의 현재 번호 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) 을 통해 유럽에서 장소의 로마 숫자(I,II,III,IV,V,etc.). 그것은 우리 모두에게 많은 문제를 저장했습니다! 레오나르도에게 감사드립니다.

피보나치 날
피보나치일은 월 23 일,그것은 자리”1,1,2,3″의 일부입니다. 그래서 다음 11 월 23 일 모두에게 알려주십시오!


Leave a Reply