에서 고전 mechanicsEdit

에 nonrelativistic 고전역학,폐쇄 시스템은 실제 시스템지 않는 교환 모든 문제와 주변지 않는 대상이 순수한 힘이 그 근원은 외부 시스템입니다. 고전 역학에서의 폐쇄 시스템은 열역학에서 고립 된 시스템과 동등 할 것이다. 닫힌 시스템은 종종 특정 문제 또는 실험의 결과에 영향을 줄 수있는 요소를 제한하는 데 사용됩니다.

in thermodynamicsEdit

속성의 격리,폐쇄하고,개방 시스템에는 교환하는 에너지 문제입니다.

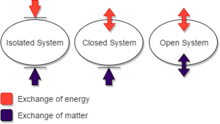
에서 열역학,닫힌 시스템을 교환할 수 있는 에너지(열 또는 작업)하지만,중요하지 않습니다.고립된 시스템을 수 없습 교환 모든 열,작업,또는 문제,주변하는 동안 열려 있는 시스템을 교환할 수 있는 에너지 문제입니다. (이 용어 정의 체계는 일부 목적에 편리하지만 균일하게 사용되지는 않습니다. 특히,일부 작가들은 여기서’고립 된 시스템’이 사용되는’폐쇄 된 시스템’을 사용합니다.)

에 대한 간단한 시스템으로의 한 유형 입자(또는 원자 분자),닫힌 시스템을 금액이 일정한 수의 입자입니다. 그러나,대한 시스템을 겪고 있는 화학 반응할 수 있습의 모든 종류의 분자 생성되고 파괴에 의해 반응 과정입니다. 이 경우에는,사실에는 시스템이 닫히 표현해는 총 수의 각 정기의 아날로그 전자기구,디지털 전자 보존된 상관없이,어떤 종류의 분자 수도 있습의 일부가 될 수 있습니다. 수학적으로:

∑j=1m i j N j=b{\displaystyle\sum_{j=1}^{m}a_{ij}N_{j}=b_{i}}

N j{\displaystyle N_{j}}

의 수 j 유형 분자,i j{\displaystyle a_{ij}}

은 수의 원자들의 요소가{\displaystyle i}

에서 분자 j{\displaystyle j}

b i{\displaystyle b_{i}}

가 총 원자의 요소가{\displaystyle i}

시스템에서는 일정하게 남아 있기 때문에,시스템이 닫힙니다. 시스템의 각기 다른 요소에 대해 그러한 방정식이 하나있을 것입니다.

열역학에서 폐쇄 시스템은 복잡한 열역학 문제를 해결하는 데 중요합니다. 그것은 따라서 그것을 단순화하는 실험 또는 문제의 결과를 바꿀 수 있는 몇몇 외부 요인의 제거를 허용합니다. 폐쇄 형 시스템은 상황을 단순화하기 위해 열역학적 평형이 필요한 상황에서도 사용될 수 있습니다.

에서는 양자 physicsEdit

이 방정식이라는 슈뢰딩거 방정식을 설명하고 동작 절연 또는 폐쇄 양자 시스템에 의해 정의하지 않는 정보를 교환(즉,에너지 및/또는 문제)다른 시스템입니다. 그래서 경우 고립된 시스템에서 몇 가지 순수 국|ψ(t)∈서 시간을,어디서 나타냅 힐베르트 공간,시스템의 시간을 발전의 상태(두 가지의 연속적인 측정).

i ℏ ∂ ∂t ψ(R,t)=h^Ψ(R,t){\displaystyle i\hbar{\frac{\partial}{\partial t}}\psi\Left(\mathbf{r},t\right)={\hat{h}}\Psi\Left(\mathbf{r},t\right)\,\!}