그래프의 선형 불평등에서 하나의 변수 번호 라인입니다. 사용하여 열기 원한<>와 폐쇄에 대한 원≤및≥.

에 대한 그래프 x>-3

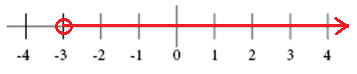
에 대한 그래프 x≥2

불가 동일한 솔루션이라고 합니다. 불평등의 속성뿐만 아니라 평등의 속성이있었습니다. 아래의 모든 속성은≥와≤를 포함하는 불평등에도 해당됩니다.

추가 제공의 불평등는 것을 말한 추가하여 같은 수의 각 측면 불평등을 생산하는 동등한 불평등

$$면\:x>y,\:다\:x+z>y+z$$

$$면\: x<y,\:다음\: x+z<y+z$$

빼기 시설의 불평등은 우리에게 빼서 같은 수의 양쪽에서 불평등은 해당하는 불평등을 겪고 있습니다.

$$면\:x>y,\:다\:x-z>y-z$$

$$면\:x<y,\:다\: x-z<y-z$$

곱셈 제공의 불평등은 우리에게는 곱셈의 양쪽에는 불평등으로 긍정적인 수를 생산하는 동등한 불평등을 겪고 있습니다.나는 이것이 어떻게 작동하는지 잘 모르겠습니다.\: z>0,\:다\:xz>yz$$

$$면\:x<y\:와\z>0,\:다\: xz<yz$$

곱에서의 각 측면 불평등으로 부정적인 숫자에 다른 손으로 생산 하지 않는 동등한 불평등하지 않는 한 우리는 또한 반대 방향으로 불평등의 기호

$$면\:x>y\:와\z<0,\:다\:xz<yz$$

$$면\:x<y\고\: z<0,\:then\:xz>yz$$

불평등의 분할 속성에 대해서도 마찬가지입니다.

양수를 갖는 불평등의 양면을 나누면 동등한 불평등이 생성됩니다.

$$면\:x>y\:와\z>0,\:다\:\frac{x}{z}>\frac{y}{z}$$

$$면\: x<y\:와\z>0,\:다음\: \frac{x}{z}<\frac{y}{z}$$

과 분할의 양쪽에는 불평등으로 부정적인 수를 생산하는 동등한 불평등으면 불평등 상징은 반대입니다.

$$면\:x>y\:와\z<0,\:다\:\frac{x}{z}<\frac{y}{z}$$

$$면\: x<y\:와\z<0,\:다\:\frac{x}{z}>\frac{y}{z}$$

를 해결하는 여러 단계 부등식으로 수행할 때 해결 멀티-단계는 답변을 받으실 수 있습니다. 변수를 상수와 분리하여 시작하는 것이 바람직 할 때 한 가지를 취하십시오. 다단계 불평등을 해결할 때 음수로 곱하거나 나눌 때 불평등 부호를 역전시키는 것을 잊지 않는 것이 중요합니다.

예

를 해결하는 불평등

$$-2\left(x+3\오른쪽)<10$$