오래된 문제가 새로운 통찰력을 얻을 수 있습니까? 아마도 4 색 정리의 우아한 증거일까요?
4 색 문제는 가장 유명한 수학 문제 중 하나입니다. 그것은 저항에 대한 증거보다 백 년 전에 마지막으로 굴복,결국가 있었고 유효한 증거,그러나 중 하나에 의존하고 천 개 이상의 시간 동안 컴퓨터 시간입니다. 짐 틸리(Jim Tilley)의 연구에 따르면 극적인 단순화가 궁극적으로 가능할 수 있습니다. 그는 발견 속에 위치하고 잠그는 최소한 습 4 컬러 정리해야 합 전시회와 공식화했다는 추측에 기반한 광범위한 조사,그 Birkhoff 다이아몬드는 유일한 기본적인 위치하고 잠그는 구성이 있습니다.
그래프 색칠은 그래프로 알려진 수학적 객체의 꼭지점에 레이블 또는 색상을 할당하는 것을 포함합니다. 4 색 문제는 대수 그래프 이론의 발전을위한 원래의 동기 중 하나를 제공했습니다. 그래프 색에 사용되는 실생활에서 접할 수 있는 대부분의 문제와 같은 충돌을 최소화를 예약할 때 스포츠 이벤트,계획 검사 시간표 및 정석,계획도 CCTV 카메라 배치를 가진 건물에 많은 구석을 최소화하기 위해 카메라의 겹칠 수 있습니다. 또한 스도쿠 퍼즐을위한 기반을 제공합니다.
4 색 문제
유명한 영국의 수학자이자 논리학자인 Augustus De Morgan 의 학생 인 Francis Guthrie 는 1852 년에 4 색 문제를 제기했습니다. 그는 공식화 문제에 관하여도 만족하는 특정 조건 등을 포함하지 않는 모든 구멍을 갖는 모든 지역(예:국가 또는 상태)에 연결되어 있는 영역에 존재하는 두 개 이상의 연속되지 않은 부분입니다. 오클라호마 주장하는 그러한 지도는 없을 개 이상의 색상의 컬러도 이러한 두가지 주변 지역이었습니다.
요즘 4 색 문제는 그래프의 관점에서 표현되며,지도에서 영역을 채색하는 대신 그래프의 정점을 한 가지 색상으로 표시합니다. 4 색 정리의 모든 기존 증명은 최소한의 반례가 존재할 수 없음을 보여줍니다. (최소 반례는 정점의 적절한 채색을 위해 4 가지 이상의 색상이 필요한 가장 작은 평면 그래프입니다.)삼각 측량이 아닌 그래프는 가장자리를 삽입하여 하나로 전환 할 수 있으므로 삼각 측량 인 평면 그래프 만 고려해야합니다. 결과 삼각 측량이 4 색이면 원래 그래프도 4 색입니다. 하나의 정밀 조사를 삼각 측량으로 제한 할 수있는 것이 매우 유용합니다.

이른 시도가 증명
의 제공하는 사람들에게 증거,알프레드는 브레이에 위치하고 있어,영어 변호사와 아마추어 수학자,던 사람이 누구의 명성분에 의해 오염된 자신의 실패한 노력이다. 그는 1879 년에 성공을 발표했으며 그의’증거’는 American Journal Of Mathematics 에 발표되었습니다. 십 년 후,그러나,다른 영어로 수학자,퍼시 Heawood,만들지도는 그는 4 색의 최종 결정에 이르기까지 영역에서 같은 방법으로 위치하고의 방법 실패에 대한 최종 지역입니다. 그의 실패에도 불구하고,Kempe 는 유용한 도구 인 Kempe 체인을 남겼습니다. 그것은 최대한의 연결(모든 꼭지점이에서 도달할 수 있는 다른 어떤 경로를 따라 가장자리)를 본다면에서는 모든 꼭지점이 사용하는 두 개의 색상입니다. Kempe 체인은 채색 및 재 채색 그래프에 도움이되는 것으로 입증되었습니다. 그림 1 을 참조하십시오.
Birkhoff diamond 만이 4-colourability 의 핵심이라면 놀라운 단순화
이 될 것입니다.
마침내 증명
첫 번째 유효한 증거는 1976 년 Kenneth Appel 과 Wolfgang Haken 에 의해 발표되었습니다. 그것은 그들의 인수의 특정 측면을 확인하기 위해 컴퓨터 시간의 천 시간 이상을 요구했다. 컴퓨터 코드에 의존하는이 개념은 잠재적으로 인간이 유발 한 오류를 포함합니다(그리고 그들의 코드는 그랬습니다!)는’인간’증거보다는 수학 공동체의 큰 부분을 만족시키지 못했습니다. 아펠과 하켄의 증거는 전체적인 구조가 우아했지만 세부 사항은 추악했습니다.
의 증거는 세련된 의해 1996 년에 팀의 네학자 로버트슨,샌더,시모어,그리고 토마스,하지만 그들은 아직도에 의존 컴퓨터 코드의 증거입니다. 2010 년 Steinberger 는 또 다른 변형을 제공했습니다. 그러나 4 색 정리가 왜 사실인지에 관해서는 완전히 만족스러운 대답은 아직 없습니다. (일단 추측이 입증되면,그것은’정리의 지위를 얻었다.’)

및 아마추어 수학자.
이 검색에 대한 대안 방지
4 색상 문제입니다 그래서 쉽게 분명히 말하고 이해하는 그의 관심을 끌었다 많은 수천의 아마추어 수학자들은 모든 믿는 것은 그들이 찾을 수 있습니다 간단적인 증거하고 따라서 유명한이 될 수 있습니다. 1978-1984 년 캐나다 왕립 군사 대학의 물리학 자이자 교장 인 짐 틸리의 아버지는 그러한 몽상가였습니다. 그가 돌파구를 만들었다 고 느낄 때마다 그는 아들 짐에게 자신의 일을 확인하라고 요청할 것입니다. 짐은 항상 결함을 발견했습니다. 아직도 불구하고,그의 초기 회의는 그의 아버지의 노력도 열매를 맺을,그가 감염되었을 가진에 대한 열정 4 색 문제를 연구하기 시작했다킬 수 있습니다.
Kempe-locking
Jim Tilley 의 연구는 4 색 정리에 대한 최소한의 반례가 전시해야하는 새로운 속성을 발견하게했습니다. 그는 그것을’Kempe-locking’이라고 명명했습니다.’그는 최소한의 반례가 전시해야하는 또 다른 재산과 양립 할 수 없을 가능성이 있음을 깨달았습니다–즉.,그래프가 어떻게 연결되어 있는지(얼마나 많은 꼭지점이 떨어져 나가기 전에 그래프에서 제거되어야하는지).
Tilley 의 Kempe-locking 은 삼각 측량의 에지와 관련된 속성입니다. 개념은 인접한 정점 x 와 y 사이의 가장자리 xy 를 삭제하는 것으로 시작합니다. 는 경우 매 4 색의 결과를 그래프에서는 색상의 x,y 같은 순서가 없다의 색 교환을에 위치하고 사슬의 원인이 되는 색상의 x 른 컬러의 y,원래 삼각했다 Kempe-잠해 xy. Tilley 증명하는 최소한 습 4 컬러 정리해야 Kempe-잠와 관련하여 모든 하나의 그것의 가장자리,모든 가장자리에 최소한 반례이 있어야합니다 채색을 제공합니다.
Kempe-locking 은 삼각 측량이 커짐에 따라 만족시키기가 더 어려워지는 특히 제한적인 조건입니다. Tilley 는 Kempe 에 잠긴 가장자리가있는 삼각 측량에 공통적 인 것이 있는지 발견하기 위해 착수했습니다. Kempe-locking 에 대한 그의 초기 검색은 그를 Birkhoff diamond 로 이끌었습니다.

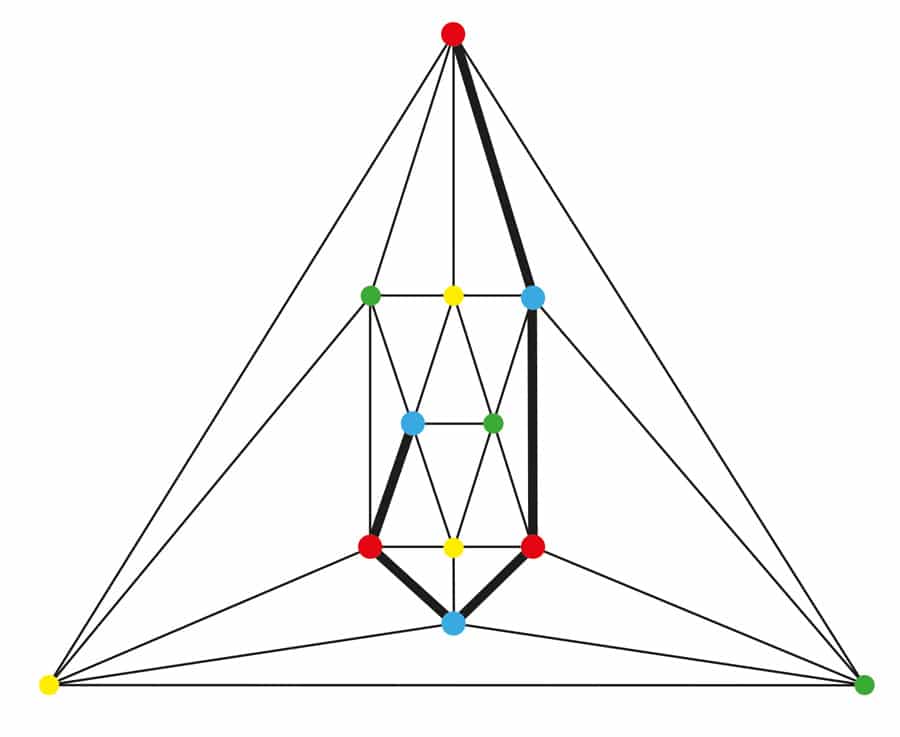
그림 3. 두 개의 평면 그래프,하나는 6 개의 꼭지점에 4 개의 연결된 삼각 측량과 17 개의 꼭지점에 5 개의 연결된 삼각 측량입니다.
The Birkhoff 다이아몬드
1913 년,G.D.Birkhoff 발견되는 특정 구성에 열국에서 지도(경계 반지의 여섯 개 국가괄하는 네 개의 국가)에 있는 중요한 제공합니다. 해당 구성이 맵에 있고 해당 구성이 제거 된 서브 맵이 4 색이면 전체 맵이 4 색이됩니다. 따라서 최소 반례는 해당 특정 구성을 포함 할 수 없습니다. 그것은 Birkhoff 다이아몬드로 알려지게되었습니다. Tilley 는 Kempe-locked edge xy 가 x 와 y 가 Birkhoff diamond 의 그래프 버전의 끝점 일 때만 발생하는 것으로 나타났습니다. 그림 2 를 참조하십시오.
추측은 쉽게 언급되고 이해할 수 있으며 흥미로 우며 모든 평면 그래프가 왜 4 색인지에 대한 강력한 설명을 제공합니다.
하지 않는 모든 위치하고 잠그는 구성 없이 Birkhoff 다이아몬드,그는 추측하는 Birkhoff 다이아몬드는 단지’기본’에 위치하고 잠그는 구성,하나는 포함되지 않은 작은 위치하고 잠그는 구성으로 를 본다면. 그러나 틸리는 자신의 비판적인 추측을 증명할 수 없다는 것을 발견했다. 사실이라면 추측이 4 색 정리를 직접 증명할 것이기 때문에 실망 스러웠습니다. (최소 반례가 되려면 삼각 측량은 Birkhoff diamond 하위 그래프를 포함해야하지만,그렇게했다면 최소 반례가 될 수 없습니다.)
압도적 인지지 사례
그의 추측을 증명하는 대신 Tilley 는 다음으로 가장 좋은 일을했습니다. 그는 실험 주의자의 역할을하고 그의 추측을 뒷받침 할 압도적 인 사례를 구축하기로 결정했습니다. 그는 나누어 모든 관련 평면 triangulations 으로 두 개의 클래스에서 그는 적어도 네 가지 꼭지점이 제거되기 전에 그래프 떨어져(4-에 연결)및 그는 적어도 다섯 개의 꼭지점이 제거되기 전에 그래프 떨어져(5-연결). 그림 3 을 참조하십시오. Tilley 의 광범위한 검색에 도움이되는 것은 각 동형 클래스(구조적으로 동일한 그래프)의 한 멤버 만 검사해야한다는 것이 었습니다. Tilley 검사는 모든 8,044isomorphism 클래스의 4-연결되어 있는 평면 triangulations 에까지 15 개의 정점과 모든 9,733isomorphism 클래스의 5-연결되어 있는 평면 triangulations 에서 24 까지 꼭지점입니다. 그는 단지 3 개의 헌병대에 잠긴 삼각 측량을 발견했습니다. 발견 된 각 Kempe-locked edge 는 Birkhoff 다이아몬드를 특징으로했으며 각각은 4 개의 연결된 삼각 측량에서 발생했습니다. 5 개의 연결된 삼각 측량 중에는 전혀 없었습니다.

Tilley 확장 검색 중에서 4 연결 triangulations 검토하여 모든 30,926isomorphism 클래스에서 16 꼭지점과 모든 158,428isomorphism 클래스에서 17 꼭지점입니다. 계산-시간 제한 것을 제한하는 그의 검색하의 샘플 100,000 임의로 생성된 non-isomorphic triangulations 각 클래스에 18,19,20 꼭지점입니다. 확장 검색 45 추가 Kempe-잠 triangulations,그러나 정확히 같은 결과로 원래 검색:각 Kempe-잠 가장자리에 삼각천하는 관련 Birkhoff 다이아몬드입니다.
여기서 어디?
Tilley 의 광범위한 검색은 Birkhoff diamond 가 근본적인 Kempe-locking 구성임을 쉽게 확인했습니다. 그는 자신의 추측을 철저히 테스트했지만 입증되지 않은 채로 남아 있습니다. 는 경우(또는 때)Tilley 의 추가 입증한 사실,즉,는 Birkhoff 다이아몬드는 혼자 열쇠 4-colourability,그것은 것은 놀라운의 단순화 문제는 하나의 구성을 설명하는 모든 것–수 있습니다.

을 증명하는 4 색 추측이 필요한 노력의 많은 저명한 수학자. Birkhoff 다이아몬드가 유일한 근본적인 Kempe-locking 구성이라는 Tilley 의 추측은 증명하기가 더 어려울 수 있습니다. 그러나 실험적 증거는 강하다. 이론가들은’왜 귀찮게합니까?’Tilley 의 대답은 만족할 줄 모르는 호기심 밖으로 이기:”모든 후에,추측은 쉽게 명시된 이해,그리고 흥미로운 제공하며,매력적인는 이유를 설명하는 모든 평면 그래프 4-colourable.”
개인적인 응답
What 처음극에 대한 열정 4 색 문제가 당신을 주도하는 연구는 그것을 그렇게 강렬?
이것은 내 아버지 집착으로 문제에서 그의 은퇴와 그의 소망을 사용하여 나를 울리는 보드에 대한 자신의 아이디어.
이 분야의 향후 연구 계획은 무엇입니까?
나는 최근에 4 색 문제에 전적으로 다른 접근법을 포함하는 복잡한 논문을 검토했다. 종이가 서있는 것처럼,나는 그것이 결함이 있다고 믿는다. 아직,그것은 약속이 있습니다. 협업을 탐구하려는 유혹을받을 수도 있습니다.
Leave a Reply