Articles

쉬운 순열과 조합

by admin

나는 항상”순열”과”조합”을 혼동했습니다.

다음은 기억하기 쉬운 방법입니다:순열은 복잡하게 들리지 않습니까? 그리고 그것은이다. 순열로 모든 작은 세부 사항이 중요합니다. 앨리스,밥과 찰리는 찰리,밥과 앨리스(여기에 친구의 이름을 삽입)다르다.반면에

조합은 꽤 쉽게 진행됩니다. 세부 사항은 중요하지 않습니다. 앨리스,밥과 찰리는 찰리,밥과 앨리스와 동일합니다.

순열은 목록(순서 문제)을위한 것이고 조합은 그룹을위한 것입니다(순서는 중요하지 않습니다).

아시다시피,”조합 잠금”은 실제로”순열 잠금”이라고해야합니다. 당신이 문제에 숫자를 넣어 순서.

쉽게 순열과 조합

진정한”조합은 잠금”을 받아들이 모두 10-17-23 및 23-17-10 으로 정확하다.

순열:털이 세부 사항

로 시작하자 순열,또는 가능한 모든 방법입니다. 우리가 사용하여 멋진 바지 용어”en”,그래서 우리는 케어에 대한 모든 세부사항을 포함해 각각의 항목입니다. 8 명이 있다고 가정 해 봅시다.

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

8 명의 참가자 중 1 위,2 위 및 3 위를 수상 할 수있는 방법은 몇 가지입니까? (Gold/Silver/청동)

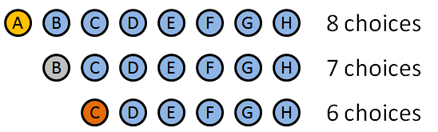
permuation 예 메달

우리는 우리가 사용하는 순열기 때문기 위해 우리는 손으로 이러한 메달 중요합니다. 다음은 그것이 분해하는 방법입니다:

  • 금메달:8 선택:A B C D E F G H(나는 이름이 어,문자와 일치 만든 방법 영리한?). A 가 금을 이긴다 고 가정 해 봅시다.
  • 은메달:7 선택:B C D E F G H.B 가 은메달을 땄다고합시다.
  • 동메달:6 선택:C D E F G H. 라고합시다…C 가 동메달을 획득합니다.

우리는 어떤 사람들이 승리,하지만 자세가 중요하지 않:우리가 선택 8 처음에 다음,7 일 후,6. 총 옵션 수는 다음과 같습니다$8 * 7 * 6 = 336$.

세부 사항을 살펴 보겠습니다. 우리는 8 명 중 3 명을 주문해야했습니다. 이를 위해 우리는 모든 옵션(8)으로 시작한 다음 메달이 다 떨어질 때까지 한 번에 하나씩(7,그 다음 6)가져갔습니다.

우리는 계승이:나는 이것이 어떻게 작동하는지 잘 모르겠습니다. =8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}

불행하게도,그것은 너무 많이! 우리는 단지$8 * 7 * 6$. 우리는 어떻게 5 에서 계승을”멈추게”할 수 있습니까?

이것은 순열이 멋지게되는 곳입니다:우리가 어떻게 없애고 싶은지 주목하십시오$5 * 4 * 3 * 2 * 1$. 이것에 대한 또 다른 이름은 무엇입니까? 5 계승!

그래서 우리가 8 을한다면!/5! 우리는 다음을 얻습니다.

\displaystyle{\frac{8!}{5!}=\frac{8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}{5\cdot4\cdot3\cdot2\cdot1}=8\cdot7\cdot6}

고 왜 우리가 사용하여 5 번? 왜냐하면 우리가 8 에서 3 개의 메달을 고른 후에 남겨 졌기 때문입니다. 따라서 이것을 작성하는 더 좋은 방법은 다음과 같습니다.

\displaystyle{\frac{8!}{(8-3)!}}

여기서 8!/(8-3)! “8 의 처음 3 개의 숫자를 사용하십시오!”라고 말하는 멋진 방법 일뿐입니다.”. 총 n 개의 항목이 있고 특정 순서로 k 를 선택하려는 경우 다음을 얻습니다.

\displaystyle{\frac{n!}{(n-k)!}}

이것은 멋진 순열식:수 있 n 항목을 찾으려면 방법의 수 k 항목을 주문할 수 있습니다.

\displaystyle{P(n,k)=\frac{n!}{(n-k)!}}

조합,호!

조합은 쉽게 진행됩니다. 순서는 중요하지 않습니다. 당신은 그것을 섞을 수 있고 똑같이 보입니다. 내가 싸구려이고 별도의 금,은 및 동메달을 감당할 수 없다고 가정 해 봅시다. 사실,나는 빈 깡통만을 감당할 수있다.

얼마나 많은 방법으로 8 명에게 3 개의 깡통을 줄 수 있습니까?이 경우 우리가 사람들을 고르는 순서는 중요하지 않습니다. 앨리스,밥,찰리에게 캔을 주면 찰리,앨리스,그리고 밥에게주는 것과 똑같습니다. 어느 쪽이든,그들은 똑같이 실망합니다.

이것은 흥미로운 점을 제기합니다-우리는 여기에 약간의 중복을 가지고 있습니다. 앨리스 밥 찰리=찰리 밥 앨리스. 잠시 동안,우리가 얼마나 많은 방법으로 3 명을 재 배열 할 수 있는지 알아 보겠습니다.첫 번째 사람에게는 3 가지 선택,두 번째 사람에게는 2 가지 선택,마지막 사람에게는 1 가지 선택 만 있습니다. 그래서 우리는$3 * 2 * 1$3 명을 다시 정렬하는 방법.

잠깐…이 순열 같은 비트를 찾고 있습니다! 날 속였어!

실제로 그랬습니다. 이 있는 경우 N 는 사람들고 당신은 방법을 알고 싶다면 많은 준비가는 그들 모두,그것의 N 계승하거나 N!

그래서,우리가 포기할 3 개의 깡통이 있다면,3 개가 있습니다! 또는 우리가 선택하는 모든 선택에 대해 6 가지 변형이 있습니다. 우리가 원하는 경우 그 밖으로 얼마나 많은 조합을 우리는,우리는 그냥 만들기 모든 순열과 분할의 모든 중복. 우리의 경우,우리는 336 개의 순열(위에서)을 얻고,각 순열에 대해 6 개의 중복으로 나누고 336/6=56 을 얻습니다.

일반 공식입니다.

\displaystyle{C(n,k)=\frac{P(n,k)}{k!}}

즉”n 에서 k 사람들을 선택하고 k 로 나누는 모든 방법을 찾으십시오! 변종”. 이것을 쓰고,우리는 우리의 조합을 수식,또는 수의 방법으로 결합 k 항목에서 설정의 n

\displaystyle{C(n,k)=\frac{n!}{(n-k)!케이!}}

때로는 C(n,k)으로 작성되:

\displaystyle{\binom{n}{k}}

는 이항 계수가 있습니다.

몇 가지 예

여기에 몇 가지 예의 조합(순서는 중요하지 않습니다)에서 순열(순서는 중요).

  • 조합:10 의 그룹에서 3 명으로 구성된 팀을 따기. $기음(10,3)=10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    순열:10 의 그룹에서 대통령,부사장 및 Waterboy 따기. $피(10,3)=10!/7! = 10 * 9 * 8 = 720$.

  • 조합:10 의 메뉴에서 3 디저트 선택. 기음(10,3)=120.

    순열:10 의 메뉴에서 순서대로 3 개의 좋아하는 디저트를 나열합니다. 피(10,3)=720.

수식을 암기하지 말고 왜 작동하는지 이해하십시오. 조합은 순열보다 간단하게 들리며,그렇습니다. 순열보다 조합이 적습니다.

다른 글에서 이 시리즈

  1. 쉽게 순열과 조합
  2. 이동 그리드를 사용하여 조합 및 순열
  3. 이해하는 방법을 조합을 사용하여 곱셈
  4. 왜 우리는 곱 조합?