복잡한 숫자:소개서(페이지 1 의 3)

섹션:소개,작업단지, 이차 공식

지금까지,당신이 말할 수 없는 광장을 가지고 뿌리의 부정적인 수입니다. 그것은 당신이 그들을 제곱 한 후에 음수 인 숫자가 없었기 때문입니다(그래서 제곱근을 취하여”뒤로 갈”수 없었습니다). 당신이 그것을 제곱 한 후에 모든 숫자는 양수였습니다. 그래서 당신은 아주 잘 네거티브를 제곱하고 현명한 것을 생각해 낼 것으로 기대할 수 없었습니다.그러나 이제 음수의 제곱근을 취할 수는 있지만 새 숫자를 사용하여 수행하는 것이 포함됩니다. 이 새로운 번호가 발명되었습니다(발견 되었습니까?)종교 개혁의 시간 주위에. 에서는 시간,아무도 믿는 모든이”현실 세계”사용에 대한 발견이 새로운 수상을 완화 계산결에 관련된 특정 방정식,그래서 새로운 수었으로 전망되고 척 수명을 위한 편의 술입니다.

(그러나,당신이 그것에 대해 생각하지 않는 모든 발명품 번호? 숫자가 나무에서 자라는 것과 같지 않습니다! 그들은 우리 머리 속에 산다. 우리는 그들 모두를 만들었습니다! 우리가 이미 가지고있는 것과 잘 작동하는 한 왜 새로운 것을 발명하지 않습니까?)

다.

지금 생각할 수 있습니다 당신은 작업을 수행 할 수 있습니다:

그러나 이해할 수 없! 당신은 이미 1 에 제곱하는 두 개의 숫자를 가지고 있습니다;즉-1 과+1. 그리고 나는 이미-1 로 제곱합니다. 그래서 나는 또한 1 로 제곱하는 것이 합리적이지 않습니다. 이것은 중요한 세부 사항을 지적합니다: 다룰 때 imaginaries,당신이 무언가를 얻을 수(처리 할 수 있는 능력을 가진 부정 내부의 제곱근),하지만 당신은 잃는 것도(일부의 유연성 및 편리하는 규칙을 사용할 때 다루는 제곱근). 특히,당신은 항상 i-PART 를 먼저해야합니다!

• Sqrt(-9)를 단순화합니다. Copyright©엘리자베스 Stapel2000-2011All Rights Reserved

(주의:이 단계를 통과하는 세 번째”같음”기호가”“,not”“. 나는 급진주의 자 밖에있다.)

• 단순화 sqrt(-25).

• 단순화 sqrt(-18).

• 단순화–sqrt(-6).

에서 당신의 계산,다룰 것이다 난 그냥 당신이 당신의 x,을 제외한다는 사실 x2 은 x2 지만,i2-1:

• 단순화 2i+3i.

2i+3i=(2+3)i=5i

• 단순화 16i–5i.

16i-5i=(16-5)i=11i

• 곱하기 및 단순화(3i)(4i).

(3i)(4i)=(3·4)(i·i)=(12)(i2) = (12)(-1) = -12

• 곱하기 및 단순화(i)(2i)(–3i).

(i)(2)(–3i)=(2·-3)(i·i·i)=(-6)(i2·i)

=(-6)(-1·i)=(-6)(–i)=6i

이 지난 문제입니다. 그 안에 i2=-1 이므로를 볼 수 있습니다. 계속,우리는 얻는다:

이 패턴의 힘,징후,1,와 나의 사이클:

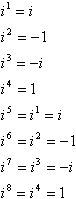
다시 말해서,계산하는 모든 고성능의 나 변환할 수 있습니다 그것은 낮은 전력해 가장 가까운 여러 개의 4 는 것 보다 더 큰 지수 및을 빼서 이러에서 지 수는 있습니다. 예를 들어,일반적인 속에서 질문한 테스트가 뭔가의 라인을 따라”단순화 i99″아이디어는 당신이 시도할 것을 곱하면 나는 아흔 아홉 번고 당신은 실행 시간,그리고 선생님을 얻을 것이 좋은 웃음서에 비용을 교수 있습니다. 여기에 어떻게 바로가기 작동합니다:

i99=i96+3=i(4×24)+3=i3=–i

는,i99=i3,할 수 있기 때문에 그냥 lop off i96. (아흔 여섯은 4 의 배수이므로 i96 은 무시할 수있는 단지 1 입니다.)즉,지수를 4 로 나누고(긴 나누기 사용)답을 버리고 나머지 만 사용할 수 있습니다. 이것은 당신에게 당신이 걱정하는 지수의 부분을 줄 것입니다. 다음은 몇 가지 더 예입니다.

• 단순화 i17.

i17=i16+1=i4·4+1=i1=i

• 단순화 i120.

i120=i4*30=i4*30+0=i0=1

• 단순화 i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>