명확한 적분
통합에 대한 소개를 먼저 읽고 싶을 수도 있습니다!
통합
|
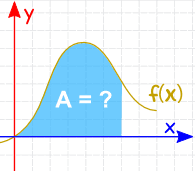
통합할 수 있습을 찾기 위해 사용될 지역,볼륨,중앙 포인트와 많은 유용한 것들입니다. 하지만 그것은 종종 사용되는 영역을 찾기 위해 아래 그래프의 기능은 다음과 같다: |
 |
|
|
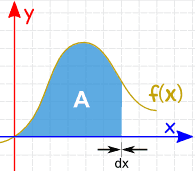
지역을 찾을 수 있습니다 추가해 슬라이스 하는 접근 방식에서 제로 폭: 가의 규칙을 통합하는 데 도움이 우리에게 응답을 얻을. |
 |
표기
기호에 대한”완전한”세련된”S”(에 대한”합”아이디어의 조각 합산):
후 필수적인 기호가 우리가 우리가 원하는 기능을 찾기 위해 필수적인 의(라는 피적분).
그런 다음 dx 로 끝내면 슬라이스가 x 방향으로 가고(너비가 0 에 접근 함)의미합니다.
명확한 적분
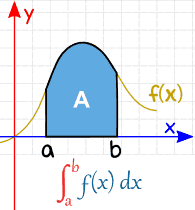
명확한 적분에는 시작 및 끝 값이 있습니다.
a 와 b(한계,경계 또는 경계라고 함)는 다음과 같이”S”의 하단과 상단에 배치됩니다:
 |
 |
|
| Definite Integral (from a to b) |
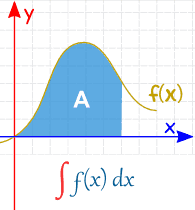
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
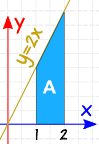
를 들어 무엇:2∫1 2 배 dx
우리는 우리 입력하라는 메시지가 표시되는 정확한 적분,1 에서 2,의 2 배 dx
먼저 우리를 찾을 필요가 무기한 중요합니다.
규칙을 사용하의 통합을 우리는 것을 발견∫2x dx=x2+C
금을 계산하는 1,2:
- x=1:∫2x dx=12+C
- x=2:∫2x dx=22+C
빼기:
“C”얻는 취소됩니다… 그래서 정확한 적분 우리는 무시할 수 있습 C.
결과:

체크인:과 같은 간단한 모양,의도를 계산하는 영역을 형상:
A= 2+42 × 1 = 3
그렇다,그것은이 지역의 3.
(야호!)
표기법: 우리가 보여줄 수 있는 부정적분(없이+C)대괄호 안에 제 a 와 b 후,다음과 같다:
를 들어(계속)
좋은 방법을 보여주신 답변:
=
다른 예를 살펴 보겠:
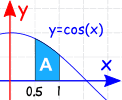
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
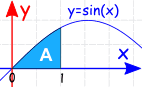
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
한정수가:∫sin(x)dx=−cos(x) +C
때문에 우리가 0 에서,우리는 단지를 계산한 필수적인 x=1?나는 이것을 할 수 없다…
뭐? 그것은 부정적인가? 그러나 그래프에서 긍정적으로 보입니다.
음… 우리는 실수를했다! 왜냐하면 x=0 에서 적분을 빼야하기 때문입니다. 우리는 그것이 0 이라고 가정해서는 안됩니다.
그래서 우리가 다른에서 하나를 빼서,제대로 할 수 있습니다:
=
그러나 우리가 할 수 있는 부정적인 영역을 때,아래의 곡선은 축
예:
정적분,1 에서 3 개,cos(x)dx:
주는 그것의 일부입니다 긍정적이며,일부 부정적이다.
확실한 적분은 순 가치를 해결할 것입니다.
우리가 계산을하자:
=
점프 -0.700 의 순 결과로 양수보다 음수가 더 많습니다….
그래서 우리는 기억해야 할 중요한 것을 가지고 있습니다:
통합을 시도 cos(x)다른 시작과 끝 값을 자신을 볼 수 있는 방법을 긍정과 부정적인 작동합니다.
긍정적인 영역
그러나 때때로 우리는 모든 영역으로 처리되는 긍정적인지(아래 부분을 차감되는 축).
경우에는 우리를 계산해야 합 지역을 별도로,같은 이 예에서는 다음과 같습니다.

예: X=1 에서 x=3 까지의 y=cos(x)와 x 축 사이의 총 면적은 얼마입니까?
이와 같은 예를 우리는 단지 않았다,그러나 지금 우리가 기대하는 모든 지역은 긍정적인(상상이 우리는 그것을 페인트).
그래서 지금 우리가 해야 할 부분을 별도:
- 한 지역에 대한 위 x-axis
- 한 지역에 대한 아래는 x-axis
곡선에 십자가 x-axis x=π/2 그래서 우리가
1π/2:
=sin(π/2)−sin(1)
from π/2to3:
=sin(3)−sin(π/2)
는 마지막 중 하나로 부정적인,하지만 우리가 원하는 것을 긍정적이다,그래서:
전체 영역=0.159… + 0.859… = 1.018…이것은 이전 예제의 대답과 매우 다릅니다.
연속
Oh yes,함수는 우리는 통합해야 지속적인 사고 b:구멍이 없는,이동 또는 수직 점근(는 기능을 머리 위/아래쪽으로 인피니티).
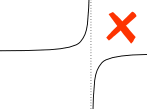
예:
수직 asymptote between a and b 영향을 미치는 확실한 중요합니다.
속성
지역에 위−아래 영역
정수 추가 위의 영역 축하지만 빼고는 지역을 아래를 위해”인터넷 가치”:
기능을 추가하
의 적분 f+g 같의 적분 f 플러스의 적분 g:
반대 간격
반대 방향으로의 간격을 제공합은 부정적인 원래의 방향이다.
![]()


Leave a Reply