コーエンのカッパを評価する

カッパの値は0未満（負）にすることができます。 スコアが0の場合は評価者間にランダムな一致があることを意味し、スコアが1の場合は評価者間に完全な一致があることを意味します。 したがって、0未満のスコアは、ランダムなチャンスよりも一致が少ないことを意味します。 以下では、これを解決するための式を示しますが、図4を理解するためには、図4を理解することが重要です。Div>

私は二つのグリッドを強調した理由は、一瞬で明らかになりますが、今のところ、私は各グリッドを分解してみましょう。p>

A=>両方の評価者が正しいと言ったインスタンスの合計数。 評価者は一致しています。P>

B=>評価者2が間違っていると言ったインスタンスの総数が、評価者1が正しいと言った。 これは意見の相違です。P>

C=>評価者1が間違っていたが、評価者2が正しいと述べたインスタンスの総数。 これも意見の相違です。

D=>両方の評価者が間違っていると言ったインスタンスの合計数。 評価者は一致しています。カッパ値を計算するには、まず合意の確率を知る必要があります（これは、合意対角を強調した理由を説明しています）。 この式は、評価者が同意するテストの数を加算し、それをテストの総数で割ることによって導出されます。 図4の例を使用すると、（A+D）/（A+B+C+D）を意味します。

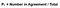
完璧です！ 次のステップは、ランダムな一致の確率を計算することです。 図4をガイドとして使用すると、期待値は、評価者1が正しいと述べた回数の合計をインスタンスの合計数で割ったもので、評価者2が正しいと述べた回の合計数をインスタンスの合計数で割ったもので、評価者1が間違っていると述べた回数の合計数に、評価者2が間違っていると述べた回数の合計数を掛けたものです。 これはそこに取り込むための多くの情報であるため、図6では上記のグリッドを使用してこの方程式を定式化しました。

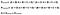
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

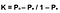
素晴らしい！ これで、信頼性と妥当性を区別し、Cohenのκを説明し、それを評価することができます。 この統計は非常に便利ですが、私はそれがどのように機能するかを理解しているので、アルゴリズムを特定の指標に最適化するときにはあまり利用されていない可能性があると信じています。 さらに、Cohenのkappaは、マルチクラス問題と不均衡なクラス問題の両方を測定するのにも適しています。

P.S. あなたは私がデータサイエンスを行うためにカバーしたい何かがある場合は、Twitterの@KurtisPykesでメッセージを私に指示するか、この記事への応答を残すことができま