Un vecchio problema produrrà una nuova intuizione? Forse un’elegante dimostrazione del teorema dei 4 colori?
Il problema a 4 colori è uno dei problemi matematici più famosi. Ha resistito alla prova per più di cento anni prima di soccombere; alla fine, c’era una prova valida, ma una che si basava su più di mille ore di tempo al computer. La ricerca di Jim Tilley suggerisce che una semplificazione drammatica potrebbe alla fine essere possibile. Ha scoperto una proprietà, Kempe-locking, che deve esibire un controesempio minimo al teorema dei 4 colori e ha formulato una congettura, basata su indagini approfondite, che il diamante Birkhoff è l’unica configurazione fondamentale di Kempe-locking.
La colorazione dei grafi comporta l’assegnazione di etichette, o colori, ai vertici di un oggetto matematico noto come grafico. Il problema a 4 colori ha fornito una delle motivazioni originali per lo sviluppo della teoria algebrica dei grafi. La colorazione dei grafici viene utilizzata in molti problemi del mondo reale, come la riduzione dei conflitti durante la pianificazione di eventi sportivi, la pianificazione degli orari degli esami e l’organizzazione di piani di posti a sedere, anche per il posizionamento di telecamere CCTV in un edificio con molti angoli al fine di ridurre al minimo la sovrapposizione delle telecamere. Esso fornisce anche le basi per i puzzle di Sudoku.
Il problema dei 4 colori
Francis Guthrie, allievo del famoso matematico e logico britannico Augustus De Morgan, pose il problema dei 4 colori nel 1852. Ha formulato il problema per quanto riguarda le mappe che soddisfano determinate condizioni, come non contenere buchi e avere ogni regione (ad esempio paese o stato) collegata in modo che nessuna regione esista in due o più parti non contigue. Guthrie ha affermato che per tali mappe non ci sarebbero mai voluti più di quattro colori per colorare la mappa in modo tale che non ci fossero due regioni vicine dello stesso colore.
Al giorno d’oggi, il problema dei 4 colori è espresso in termini di grafici, e invece di colorare le regioni nelle mappe, uno colora i vertici nei grafici. Tutte le prove esistenti del teorema dei 4 colori dimostrano che un controesempio minimo non può esistere. (Un controesempio minimo è il grafo planare più piccolo che richiede più di quattro colori per una corretta colorazione dei suoi vertici.) Devono essere considerati solo i grafici planari che sono triangolazioni, poiché qualsiasi grafico che non sia una triangolazione può essere trasformato in uno inserendo i bordi. Se la triangolazione risultante è 4-colourable, allora anche il grafico originale è 4-colourable. È molto utile essere in grado di limitare il proprio controllo alle triangolazioni.

Un primo tentativo di prova
Di coloro che hanno offerto una prova, Alfred Bray Kempe, un avvocato inglese e matematico dilettante, è stata la persona la cui reputazione è stata più contaminata dal suo sforzo fallito. Ha annunciato il suo successo nel 1879 e la sua ‘prova’ è stato pubblicato nel American Journal of Mathematics. Undici anni dopo, però, un altro matematico inglese, Percy Heawood, ha creato una mappa che ha 4-colorato fino alla regione finale in modo tale che il metodo di Kempe fallito per quella regione finale. Nonostante il suo fallimento, Kempe ha lasciato uno strumento utile: una catena Kempe. È un sottografo massimo, connesso (ogni vertice raggiungibile da qualsiasi altro da un percorso lungo i bordi) in cui tutti i vertici usano esattamente due colori. Le catene Kempe si sono dimostrate fondamentali nella colorazione e nella ricolorazione dei grafici. Vedere Figura 1.
Sarebbe una semplificazione sorprendente
se il diamante Birkhoff da solo è la chiave per la 4-colorabilità.
Prova finalmente
La prima prova valida fu annunciata nel 1976 da Kenneth Appel e Wolfgang Haken. Ha richiesto oltre mille ore di tempo al computer per verificare aspetti particolari della loro argomentazione. Questa nozione di fare affidamento sul codice del computer, potenzialmente contenente errori indotti dall’uomo (e il loro codice lo ha fatto!), piuttosto che una prova ‘umana’, non ha soddisfatto gran parte della comunità matematica. La prova di Appel e Haken era elegante nella sua struttura complessiva, ma i dettagli erano brutti.
La prova è stata perfezionata nel 1996 da un team di quattro matematici: Robertson, Sanders, Seymour e Thomas, ma hanno ancora fatto affidamento sul codice del computer per completare la loro prova. Nel 2010, Steinberger ha offerto un’altra variante. Tuttavia, non esiste ancora una risposta completamente soddisfacente sul perché il teorema dei 4 colori sia vero. (Una volta che la congettura è stata dimostrata, ha guadagnato lo status di un ‘teorema.’)

e matematico dilettante.
La ricerca di una prova alternativa
Il problema dei 4 colori è così facile da articolare e comprendere che ha attirato l’interesse di molte migliaia di matematici dilettanti, tutti convinti di poter trovare una semplice prova classica e quindi diventare famosi. Il padre di Jim Tilley, fisico e preside del Royal Military College canadese dal 1978 al 1984, era uno di questi sognatori. Ogni volta che sentiva di aver fatto una svolta, chiedeva a suo figlio, Jim, di controllare il suo lavoro. Jim ha sempre trovato un difetto. Eppure, nonostante il suo iniziale scetticismo sul fatto che gli sforzi di suo padre avrebbero mai dato i loro frutti, fu contagiato dall’entusiasmo per il problema dei 4 colori e iniziò a studiarlo intensamente.
Kempe-locking
La ricerca di Jim Tilley ha portato alla sua scoperta di una nuova proprietà che un controesempio minimo al teorema dei 4 colori deve esibire. L’ha chiamata “Kempe-locking”.”Si rese conto che era probabile che fosse incompatibile con un’altra proprietà che un controesempio minimo dovesse esibire – vale a dire., quanto è collegato un grafico (quanti vertici devono essere rimossi da un grafico prima che cada a pezzi).
Il Kempe-locking di Tilley è una proprietà associata a un bordo in una triangolazione. La nozione inizia con l’eliminazione di un bordo xy tra i vertici adiacenti x e y. Se per ogni 4 colori del grafico risultante in cui i colori di x e y sono uguali, non esiste una sequenza di scambi di colori sulle catene di Kempe che fa sì che il colore di x differisca dal colore di y, allora la triangolazione originale si dice che sia bloccata da Kempe rispetto al bordo xy. Tilley ha dimostrato che un controesempio minimo al teorema dei 4 colori deve essere Kempe-locked rispetto a ciascuno dei suoi bordi; ogni bordo in un controesempio minimo deve avere questa proprietà colorante.
Il Kempe-locking è una condizione particolarmente restrittiva che diventa più difficile da soddisfare man mano che una triangolazione diventa più grande. Tilley ha deciso di scoprire se c’è qualcosa di comune alle triangolazioni che hanno bordi bloccati da Kempe. La sua prima ricerca di Kempe-bloccaggio lo ha portato al diamante Birkhoff.

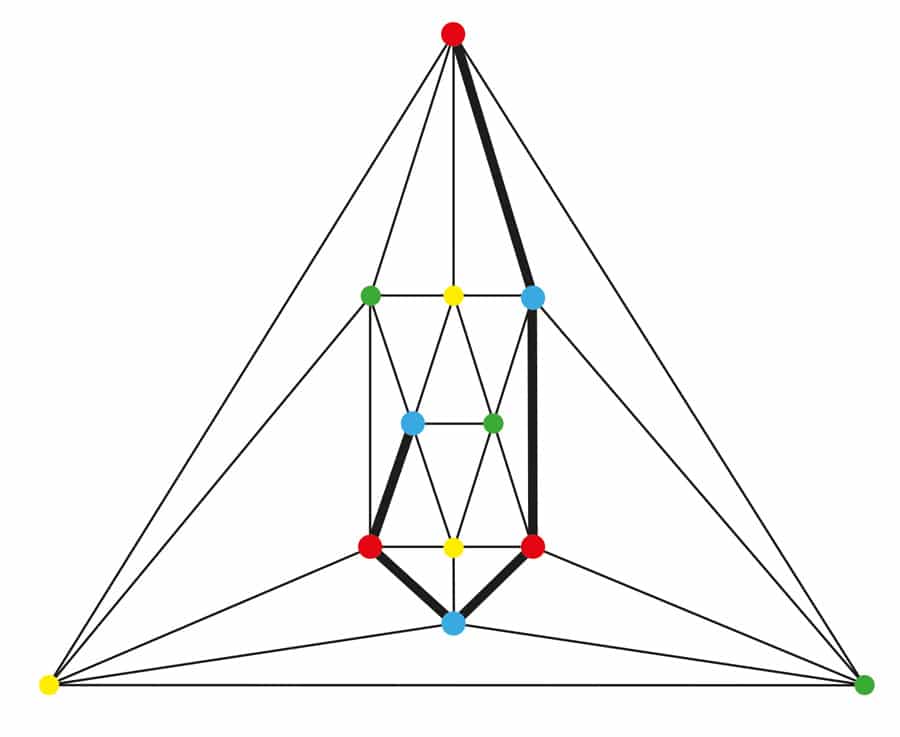
Figura 3. Due grafi planari, uno a 4-collegato triangolazione su 6 vertici e uno a 5-collegato triangolazione su 17 vertici.
Il diamante Birkhoff
Nel 1913, G. D. Birkhoff scoprì che una certa configurazione di dieci paesi in una mappa (un anello di confine di sei paesi che racchiude un insieme di quattro paesi) ha una proprietà importante. Se quella configurazione è presente in una mappa e se la sottomappa con quella configurazione rimossa è 4-colourable, allora l’intera mappa sarà 4-colourable. Pertanto, un controesempio minimo non può contenere quella particolare configurazione. È venuto per essere conosciuto come il diamante Birkhoff. Tilley ha scoperto che un bordo xy bloccato da Kempe sembra sorgere solo quando x e y sono anche gli endpoint della versione del grafico di un diamante Birkhoff. Vedi Figura 2.
La congettura è facilmente enunciabile, comprensibile e intrigante, e offre una spiegazione convincente per il motivo per cui tutti i grafici planari sono 4-colourable.
Non avendo incontrato alcuna configurazione di blocco Kempe senza un diamante Birkhoff, ha congetturato che il diamante Birkhoff è l’unica configurazione di blocco Kempe ‘fondamentale’, una che non contiene una configurazione di blocco Kempe più piccola come sottografo. Tuttavia, Tilley ha scoperto che non poteva dimostrare la sua congettura critica. Era frustrante perché, se fosse vero, la congettura avrebbe dimostrato direttamente il teorema dei 4 colori. (Per essere un controesempio minimo, una triangolazione dovrebbe contenere un sottografo di diamante Birkhoff, ma se lo facesse, non potrebbe essere un controesempio minimo.)
Un caso di supporto travolgente
Invece di dimostrare la sua congettura, Tilley ha fatto la cosa migliore. Decise di interpretare il ruolo di uno sperimentalista e costruire un caso travolgente per sostenere la sua congettura. Ha diviso tutte le triangolazioni planari rilevanti in due classi: quelle in cui almeno quattro vertici devono essere rimossi prima che i grafici cadano a pezzi (4-collegati) e quelle in cui almeno cinque vertici devono essere rimossi prima che i grafici cadano a pezzi (5-collegati). Vedere Figura 3. Utile nella vasta ricerca di Tilley era che doveva esaminare solo un membro di ogni classe di isomorfismo (grafici che sono strutturalmente identici). Tilley ha esaminato tutte le 8.044 classi di isomorfismo di triangolazioni planari a 4 connessioni su un massimo di 15 vertici e tutte le 9.733 classi di isomorfismo di triangolazioni planari a 5 connessioni su un massimo di 24 vertici. Ha trovato solo tre triangolazioni bloccate da Kempe. Ogni bordo scoperto bloccato da Kempe presentava un diamante Birkhoff e ciascuno si verificava in una triangolazione a 4 connessioni. Non ce n’erano affatto tra le triangolazioni a 5 connessioni.

Tilley espanse la sua ricerca tra triangolazioni a 4 connessioni esaminando tutte le 30.926 classi di isomorfismo su 16 vertici e tutte le 158.428 classi di isomorfismo su 17 vertici. Le limitazioni del tempo di calcolo significavano limitare la sua ricerca a campioni di triangolazioni non isomorfe generate casualmente da 100.000 ciascuna per classi su 18,19 e 20 vertici. La ricerca estesa ha rivelato 45 triangolazioni aggiuntive bloccate da Kempe, ma esattamente gli stessi risultati della ricerca originale: ogni bordo bloccato da Kempe in una triangolazione presentava un diamante Birkhoff associato.
Dove da qui?
Le ricerche approfondite di Tilley hanno facilmente confermato che il diamante Birkhoff è una configurazione fondamentale per il bloccaggio del Kempe. Ha accuratamente testato la sua congettura, ma rimane non provata. Se (o quando) la congettura di Tilley è dimostrata vera, cioè che il diamante Birkhoff da solo è la chiave per la 4-colorabilità, sarebbe una sorprendente semplificazione del problema: una singola configurazione che spiega tutto – l’eleganza matematica.

La dimostrazione della congettura a 4 colori richiese gli sforzi di molti eminenti matematici. La congettura di Tilley secondo cui il diamante Birkhoff è l’unica configurazione fondamentale di Kempe-locking potrebbe essere ancora più difficile da dimostrare. Tuttavia, le prove sperimentali sono forti. I teorici potrebbero dire ‘ perché preoccuparsi?”La risposta di Tilley è che insaziabile curiosità vincerà:” Dopo tutto, la congettura è facilmente affermabile, comprensibile e intrigante, e offre una spiegazione convincente per il motivo per cui tutti i grafici planari sono 4-colourable.”
Risposta personale
Cosa ha inizialmente spinto il tuo entusiasmo per il problema dei 4 colori e ti ha portato a studiarlo così intensamente?
Era l’ossessione di mio padre per il problema nella sua pensione e il suo desiderio di usare me come cassa di risonanza per le sue idee.
Quali sono i tuoi piani per la ricerca futura in questo settore?
Ho recentemente esaminato un documento complicato che coinvolge un approccio completamente diverso al problema dei 4 colori. Come la carta sta, credo che abbia difetti. Eppure, ha promessa. Potrei essere tentato di esplorare una collaborazione.
Leave a Reply