Sequenza di Fibonacci
La sequenza di Fibonacci è la serie di numeri:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Il prossimo numero si trova sommando i due numeri precedenti di esso:
- il 2 si trova sommando i due numeri prima di (1+1),
- il 3 si trova sommando i due numeri prima di (1+2),
- il 5 (2+3),
- e così via!
Esempio: il numero successivo nella sequenza sopra è 21+34 = 55
È così semplice!
Ecco una lista più lunga:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
Riesci a capire i prossimi numeri?
Crea una spirale
Quando facciamo quadrati con quelle larghezze, otteniamo una bella spirale:
Vedi come i quadrati si adattano perfettamente insieme?
Per esempio 5 e 8 fanno 13, 8 e 13 fanno 21, e così via.

Questa spirale si trova in natura!
Vedi: Natura, Il Rapporto aureo e Fibonacci
La Regola
La Sequenza di Fibonacci può essere scritta come una “Regola” (vedi Sequenze e Serie).
Innanzitutto, i termini sono numerati da 0 in poi in questo modo:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
Quindi il termine numero 6 è chiamato x6 (che equivale a 8).
|
Esempio: l ‘ 8 ° termine è x8 = x7 + x6 |
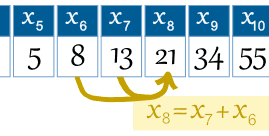 |
in Modo che possiamo scrivere la regola:
La Regola è xn = xn−1 + xn−2
dove:
- xn è termine numero “n”
- xn−1 è il termine precedente (n−1)
- xn−2 è il termine prima che (n−2)
Esempio: durata 9 è così calcolato:
Golden Ratio
E qui è una sorpresa. Quando prendiamo due numeri di Fibonacci successivi (uno dopo l’altro), il loro rapporto è molto vicino al rapporto aureo “φ” che è circa 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
non Dobbiamo iniziare con 2 e 3, qui ho casualmente scelto 192 e 16 (e ottenuto la sequenza 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
Ci vuole più tempo per ottenere buoni valori, ma dimostra che non solo la sequenza di Fibonacci può farlo!
Usando il Rapporto aureo per calcolare i numeri di Fibonacci
E ancora più sorprendente è che possiamo calcolare qualsiasi numero di Fibonacci usando il Rapporto aureo:
xn = φn − (1−φ)n√5
La risposta esce come un numero intero, esattamente uguale all’aggiunta dei due termini precedenti.
Esempio: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
Quando ho usato una calcolatrice su questo (inserendo solo il rapporto aureo a 6 cifre decimali) Ho ottenuto la risposta 8.00000033 , un calcolo più accurato sarebbe più vicino a 8.
Prova n=12 e vedi cosa ottieni.
Puoi anche calcolare un numero di Fibonacci moltiplicando il precedente numero di Fibonacci per il rapporto aureo e quindi arrotondando (funziona per numeri superiori a 1):
Esempio: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (arrotondato)
Alcune cose interessanti
Ecco di nuovo la sequenza di Fibonacci:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
C’è un modello interessante:
- Guarda il numero x3 = 2. Ogni 3 ° numero è un multiplo di 2 (2, 8, 34, 144, 610, …)
- Guarda il numero x4 = 3. Ogni 4 ° numero è un multiplo di 3 (3, 21, 144,…)
- Guarda il numero x5 = 5. Ogni 5 ° numero è un multiplo di 5 (5, 55, 610, …)
E così via (ogni ennesimo numero è un multiplo di xn).
1/89 = 0.011235955056179775…
Nota le prime cifre (0,1,1,2,3,5) sono la sequenza di Fibonacci?
In un certo senso lo sono tutti, tranne che i numeri a più cifre (13, 21, ecc.) si sovrappongono, in questo modo:
… ecc…
0,011235955056179775… = 1/89
Condizioni Sotto Zero
La sequenza di opere sotto lo zero anche, come questo:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Dimostra a te stesso che ogni numero viene trovato sommando i due numeri prima di esso!)
Infatti la sequenza sotto lo zero ha gli stessi numeri della sequenza sopra lo zero, tranne che seguono un +-+- … modello. Può essere scritto in questo modo:
x−n = (-1)n+1 xn
Che dice che il termine “−n” è uguale a (-1)n+1 volte il termine “n”, e il valore (-1)n + 1 rende ordinatamente il corretto +1, -1, +1, -1, … modello.
Storia
Fibonacci non è stato il primo a conoscere la sequenza, era conosciuto in India centinaia di anni prima!

A proposito di Fibonacci L’uomo
Il suo vero nome era Leonardo Pisano Bogollo, e visse tra il 1170 e il 1250 in Italia.
“Fibonacci” era il suo soprannome, che significa approssimativamente “Figlio di Bonacci”.
Oltre ad essere famoso per la sequenza di Fibonacci, ha contribuito a diffondere i numeri indù-arabi (come i nostri numeri attuali 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) attraverso l’Europa al posto dei numeri romani (I, II, III, IV, V, ecc.). Questo ci ha salvato un sacco di guai! Grazie Leonardo.

Fibonacci Day
Fibonacci Day è il 23 novembre, in quanto ha le cifre “1, 1, 2, 3” che fa parte della sequenza. Così il prossimo novembre 23 far sapere a tutti!


Leave a Reply