Il grafico di una disuguaglianza lineare in una variabile è una linea numerica. Utilizzare un cerchio aperto per <e> e un cerchio chiuso per ≤ e ≥.

Il grafico per x > -3

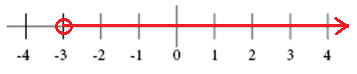
Il grafico per x ≥ 2

le Disuguaglianze che hanno la stessa soluzione sono chiamati equivalente. Ci sono proprietà di disuguaglianze così come c’erano proprietà di uguaglianza. Tutte le proprietà di seguito sono valide anche per le disuguaglianze che coinvolgono ≥ e ≤.

L’aggiunta di proprietà della disuguaglianza dice che l’aggiunta lo stesso numero per ogni lato della disuguaglianza produce un equivalente disuguaglianza

$$Se \: x>y,\: poi\: x+z>y+z$$

$$Se\: x<y,\: quindi\: x + z < y+z

La proprietà di sottrazione della disuguaglianza ci dice che sottraendo lo stesso numero da entrambi i lati di una disuguaglianza si ottiene una disuguaglianza equivalente.

$$Se \: x>y,\: poi\: x-z>y-z$$

$$Se\: x<y,\: poi\: x-z<y-z$$

La moltiplicazione di proprietà della disuguaglianza ci dice che la moltiplicazione su entrambi i lati di una disequazione con un numero positivo produce un equivalente di disuguaglianza.

If If\: x> y\: e\: z>0,\: poi\: xz>yz$$

$$Se\: x<y\: e\: z>0,\: poi\: xz<yz$$

la Moltiplicazione in ogni lato di una disuguaglianza con un numero negativo invece non produce un equivalente di disuguaglianza a meno che non abbiamo anche invertire la direzione della disuguaglianza

$$Se \: x>y \: e\: z<0,\: poi\: xz<yz$$

$$Se\: x<y\: e\: z<0,\: then\: xz>yz

Lo stesso vale per la proprietà di divisione della disuguaglianza.

La divisione di entrambi i lati di una disuguaglianza con un numero positivo produce una disuguaglianza equivalente.

$$Se \: x>y \: e\: z>0,\: poi\: \frac{x}{z}>\frac{y}{z}$$

$$Se\: x<y\: e\: z>0,\: quindi\: \frac {x} {z} <\frac{y}{z}

E la divisione su entrambi i lati di una disuguaglianza con un numero negativo produce una disuguaglianza equivalente se il simbolo di disuguaglianza è invertito.

$$Se \: x>y \: e\: z<0,\: poi\: \frac{x}{z}<\frac{y}{z}$$

$$Se\: x<y\: e\: z<0,\: poi\: \frac{x}{z}>\frac{y}{z}$$

Per risolvere un multi-step di disuguaglianza è fare come hai fatto tu quando la risoluzione multi-step di equazioni. Prendi una cosa alla volta preferibilmente iniziando isolando la variabile dalle costanti. Quando si risolvono disuguaglianze multi-step è importante non dimenticare di invertire il segno di disuguaglianza quando si moltiplicano o si dividono con numeri negativi.

Esempio

Risolvi la disuguaglianza

$ $ -2\left ( x+3 \right)< 10