i Numeri Complessi: Introduzione (pagina 1 di 3)

Sezioni: Introduzione, Operazioni con i complessi La Formula Quadratica

Fino ad ora, è stato detto che non si può prendere la radice quadrata di un numero negativo. Questo perché non avevi numeri negativi dopo averli squadrati (quindi non potevi “tornare indietro” prendendo la radice quadrata). Ogni numero era positivo dopo che l’hai squadrato. Quindi non potresti benissimo quadrare un negativo e aspettarti di trovare qualcosa di sensato.

Ora, tuttavia, puoi prendere la radice quadrata di un numero negativo, ma implica l’uso di un nuovo numero per farlo. Questo nuovo numero è stato inventato (scoperto?) intorno al tempo della Riforma. A quel tempo, nessuno credeva che qualsiasi uso del “mondo reale” sarebbe stato trovato per questo nuovo numero, oltre a facilitare i calcoli coinvolti nella risoluzione di alcune equazioni, quindi il nuovo numero è stato visto come un numero finto inventato per convenienza.

(Ma poi, quando ci pensi, non sono invenzioni tutti i numeri? Non è come se i numeri crescessero sugli alberi! Vivono nelle nostre teste. Li abbiamo inventati tutti! Perché non inventarne uno nuovo, purché funzioni bene con quello che abbiamo già?)

Quindi:

Ora, si potrebbe pensare che si può fare in questo modo:

Ma questo non ha alcun senso! Hai già due numeri che quadrano a 1; vale a dire -1 e +1. E ho già quadrati a -1. Quindi non è ragionevole che vorrei anche quadrato a 1. Questo sottolinea un dettaglio importante: Quando si ha a che fare con gli immaginari, si guadagna qualcosa (la capacità di affrontare i negativi all’interno delle radici quadrate), ma si perde anche qualcosa (alcune delle flessibilità e delle regole convenienti che si avevano quando si trattava di radici quadrate). In particolare, DEVI SEMPRE FARE PRIMA L’i-PART!

• Semplifica sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Tutti i diritti riservati

(Attenzione: il passaggio che passa attraverso il terzo segno “uguale” è ” “, non ““. L’io è al di fuori del radicale.)

• Semplifica sqrt(-25).

• Semplifica sqrt(-18).

• Semplifica –sqrt(-6).

i calcoli, avrete a che fare con i proprio come si farebbe con x, tranne per il fatto che x2 è solo x2, ma i2 è -1:

• Semplificare 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• Semplificare 16i – 5i.

16i – 5i = (16 – 5)i = 11i

• Moltiplicare e semplificare (3i)(4i).

(3i)(4i) = (3·4) (i·i) = (12) (i2) = (12)(-1) = -12

• Moltiplica e semplifica (i) (2i) (–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

Notare questo ultimo problema. Al suo interno, puoi vedere che , perché i2 = -1. Continuando, otteniamo:

Questo modello di poteri, segni, 1, e io è un ciclo:

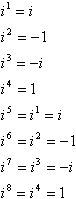
In altre parole, per calcolare alta potenza di i, è possibile convertirla in una potenza inferiore, prendendo il più vicino multiplo di 4, che è più grande di esponente e sottraendo questo di più dall’esponente. Ad esempio, una domanda trabocchetto comune sui test è qualcosa sulla falsariga di “Semplificare i99”, l’idea è che proverai a moltiplicare i novantanove volte e finirai il tempo, e gli insegnanti avranno una buona risatina a tue spese nel salone della facoltà. Ecco come funziona il collegamento:

i99 = i96+3 = io(4×24)+3 = i3 = –i

Questo è, i99 = i3, perché si può solo lop fuori la i96. (Novantasei è un multiplo di quattro, quindi i96 è solo 1, che puoi ignorare.) In altre parole, puoi dividere l’esponente per 4 (usando la divisione lunga), scartare la risposta e usare solo il resto. Questo ti darà la parte dell’esponente che ti interessa. Ecco alcuni altri esempi:

• Semplifica i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• Semplificare i120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• Semplificare i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>