La matematica è più una maratona che uno sprint — è un lungo, lento e costante grind, con rari momenti di svolta. Eppure, di tanto in tanto, otteniamo quei preziosi momenti “Eureka”, quelle brevi righe di lettere e numeri che cambiano la scienza per sempre. Ecco alcune delle equazioni più famose, dagli antichi greci alla fisica moderna.

Teorema di Pitagora (530 AC)

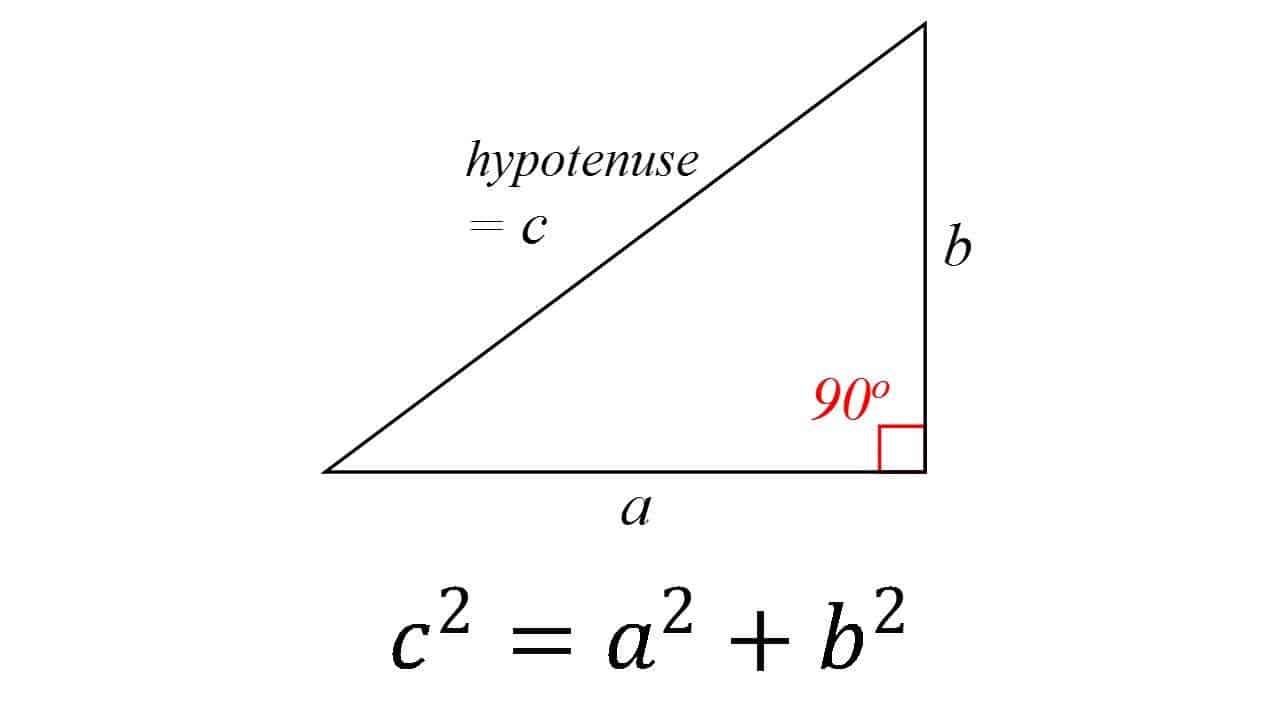
Questo è piuttosto uno dei pilastri fondanti tutta la geometria: in un triangolo rettangolo, il quadrato dell’ipotenusa (il lato opposto all’angolo retto) è uguale alla somma dei quadrati degli altri due. La teoria è generalmente attribuita al matematico greco Pitagora, anche se ci sono alcune prove che i matematici babilonesi capito la formula. È anche molto probabile che il teorema fosse conosciuto da molte persone, ma fu il primo a dimostrarlo.

Il teorema è stato dato numerose prove — forse la maggior parte per qualsiasi teorema matematico. Essi sono molto diverse, tra cui sia prove geometriche e prove algebriche,con alcuni incontri migliaia di anni.

Numeri complessi

Il matematico italiano Gerolamo Cardano è il primo ad aver introdotto numeri complessi, definendoli all’epoca “fittizi”. Tuttavia, lo sviluppo matematico di ” i ” come numero immaginario che rappresenta la radice quadrata di -1 è attribuito a Leonhard Euler, uno dei più importanti matematici e scienziati della storia umana.

I numeri complessi sono fondamentalmente numeri che non esistono realmente, ma che sono molto utili per una serie di calcoli. Sono costituiti da numeri con una parte reale (i numeri che tutti conosciamo) e una parte immaginaria (l’io rappresentato qui) e hanno applicazioni pratiche in molti campi, tra cui fisica, chimica, biologia, economia, ingegneria elettrica e statistica.

logaritmi

i Logaritmi sono fondamentalmente la funzione inversa dell’elevamento a potenza. Avete bisogno di un numero (N), base (a), e il logaritmo di N in base a sarà di x, dove N è uguale a una potenza di x. Potrebbe sembrare solo un modo diverso di scrivere la stessa cosa (e in un certo senso, lo è), ma i logaritmi sono una miriade di applicazioni pratiche, di essere utilizzati in psicologia, economia, e le misure di molti fenomeni fisici (come il pH o la magnitudo di un terremoto).

I logaritmi furono pubblicamente proposti da John Napier nel 1614, in un libro intitolato Mirifici Logarithmorum Canonis Descriptio (Descrizione della meravigliosa regola dei logaritmi) — un titolo appropriato. Un caso speciale di logaritmo è il logaritmo naturale-e, dove e è un numero irrazionale e trascendentale approssimativamente uguale a 2,71828182845. In effetti, e stessa ha una storia affascinante e un numero impressionante di applicazioni, ma questa è una storia per un’altra volta.

Calcolo

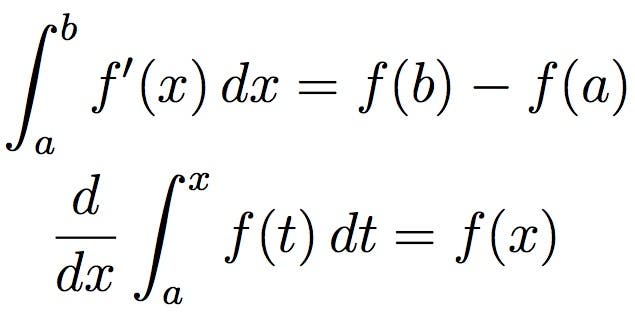
Pochi campi della matematica hanno avuto l’impatto del calcolo. Sviluppato nel 17 ° secolo da Isaac Newton e Gottfried Wilhelm Leibniz, il calcolo è ampiamente usato nella scienza, nell’ingegneria e nell’economia. Il calcolo di solito si concentra sul trattare con piccole quantità, in particolare quantità infinitamente piccole. Attraverso il calcolo, questi possono essere trattati come numeri reali, anche se sono tecnicamente infinitamente piccoli.

Per una visualizzazione più semplice, l’integrazione, descritta sopra, può essere pensata come la misurazione dell’area sotto una curva, definita da una funzione.

La legge di gravità

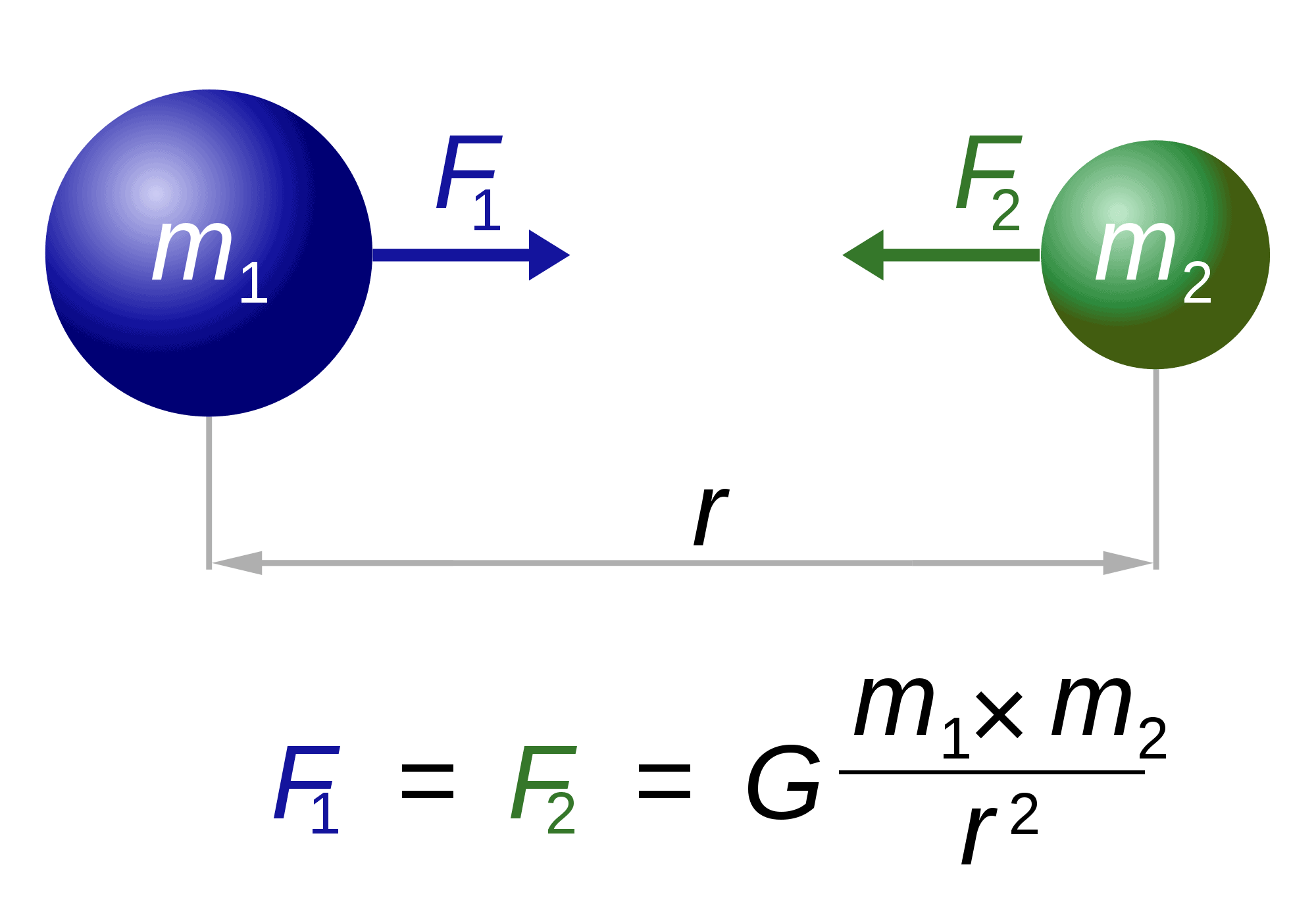
Parlando di Newton, è anche “responsabile” di una delle equazioni più famose e spettacolari del mondo: la legge di gravità.

La legge descrive fondamentalmente come due corpi di masse m1 e m2 siano attratti l’uno dall’altro. La forza (F1, F2) è inversamente proporzionale al quadrato della distanza tra loro (r). L’unico fattore rimasto, G, è una costante gravitazionale. La natura di questa costante rimane inafferrabile.

Relatività Generale

Per quasi 200 anni, la legge di Newton ha definito il nostro livello di comprensione della meccanica. Il lavoro di Einstein nel 20 ° secolo ha portato le cose al livello successivo: questi due risultati si ergono sui piedistalli più alti del mondo della fisica.

La relatività generale è essenzialmente una teoria geometrica della gravitazione, generalizzando la teoria di Newton che fornisce una descrizione unificata della gravità come proprietà geometrica dello spazio e del tempo o dello spaziotempo. In particolare, Einstein ha mostrato non solo che esiste una cosa come “spaziotempo” che fonde le tre dimensioni con la 4a dimensione del tempo, ma ha anche mostrato che questo spaziotempo può essere curvato dalla gravità, con la curvatura direttamente correlata all’energia e al momento di qualsiasi materia e radiazione siano presenti.

Seconda legge della termodinamica

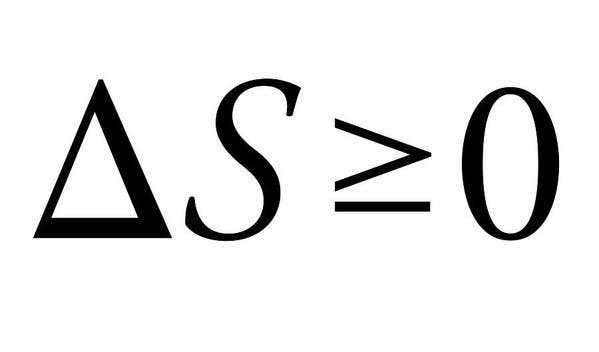
La seconda legge della termodinamica è il motivo per cui non possiamo avere cose belle nell’Universo. Scherzi a parte, le quattro leggi della termodinamica definiscono grandezze fisiche fondamentali (temperatura, energia ed entropia) che caratterizzano i sistemi termodinamici. Il secondo, in particolare, si distingue qui per la sua semplicità, ma implicazioni assolutamente massicce.

La legge stabilisce essenzialmente che la somma delle entropie dei sistemi termodinamici interagenti deve sempre aumentare, o al massimo rimanere costante. Quando l’energia cambia da una forma all’altra o la materia si muove, l’entropia (o disturbo) in un sistema chiuso aumenta. Tutte le differenze di temperatura, pressione e densità tendono a appiattirsi dopo un po ‘

Equazioni di Maxwell

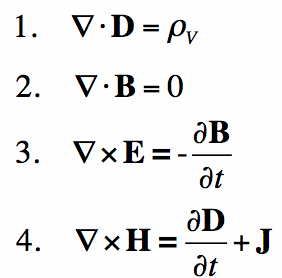
In poche parole, le equazioni di Maxwell sono per l’elettromagnetismo ciò che la legge di Newton è per la meccanica. Forniscono una base matematica per l’elettromagnetismo classico, l’ottica classica e i circuiti elettrici. Essi sono ampiamente utilizzati nel dispositivo molto si sta leggendo questo su-fondamentalmente, tutti i dispositivi elettronici.

Le leggi di Maxwell descrivono come i campi elettrici e magnetici sono generati da cariche, correnti e cambiamenti dei campi. Una svolta significativa è stata la dimostrazione che i campi elettrici e magnetici si propagano alla velocità della luce.

di Eulero Identità

Infine, questo è forse il più elegante equazione, una cosa di bellezza suprema, perché riguarda tutti i “basic” numeri:

• 0, che è neutro per l’addizione e la sottrazione;
• 1, che è neutro per la moltiplicazione e la divisione;
• e, che è di Eulero numero (vedi sopra), la base dei logaritmi naturali;
• i è l’unità immaginaria (vedi sopra); e
• π è pi, il rapporto tra la circonferenza di un cerchio e il suo diametro.

Trovare una relazione che unifichi tutti questi numeri è a dir poco mozzafiato e sembra piuttosto improbabile. La dimostrazione non è esattamente semplice, ma puoi vederla qui.

e ‘ giusto che l’Università di Stanford professore di matematica Keith Devlin descritto l’equazione, dicendo che “come un sonetto Shakespeariano, che cattura l’essenza dell’amore, o un quadro che mette in risalto la bellezza della forma umana che è molto di più che solo la pelle in profondità, equazione di Eulero si raggiunge scendendo nelle profondità dell’esistenza”

non È spesso che la matematica e la fisica, si riducono a semplici ed eleganti equazioni, ma quando lo fanno, che spettacolo per gli occhi.