Introduzione

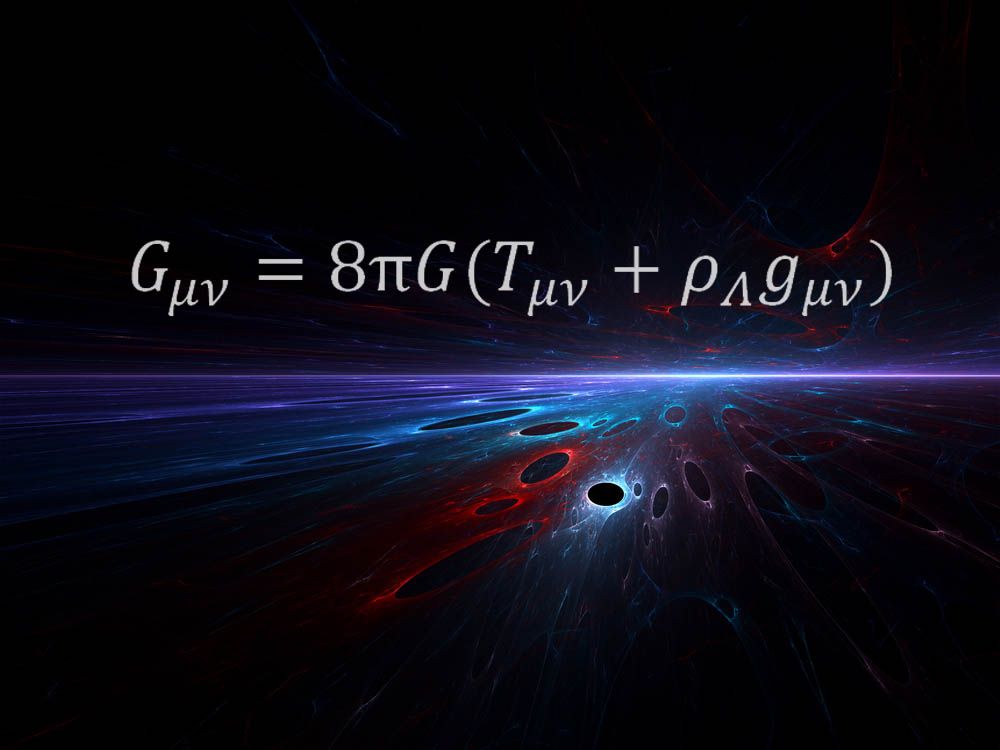
equazioni Matematiche non sono solo utili, molti sono abbastanza belle. E molti scienziati ammettono di amare spesso formule particolari non solo per la loro funzione, ma per la loro forma e le semplici verità poetiche che contengono.

Mentre alcune equazioni famose, come E = mc^2 di Albert Einstein, hog la maggior parte della gloria pubblica, molte formule meno familiari hanno i loro campioni tra gli scienziati. LiveScience ha chiesto fisici, astronomi e matematici per il loro preferito equazioni; ecco cosa abbiamo trovato:

la relatività Generale

L’equazione di cui sopra è stata formulata da Einstein come parte della sua rivoluzionaria teoria della relatività generale nel 1915. La teoria rivoluzionò il modo in cui gli scienziati comprendevano la gravità descrivendo la forza come una deformazione del tessuto dello spazio e del tempo.

“E’ ancora sorprendente per me che una tale equazione matematica può descrivere ciò che lo spazio-tempo è tutto”, ha detto Space Telescope Science Institute astrofisico Mario Livio, che ha nominato l’equazione come il suo preferito. “Tutto il vero genio di Einstein è incarnato in questa equazione.”

” Il lato destro di questa equazione descrive il contenuto energetico del nostro universo (inclusa l ‘”energia oscura” che spinge l’attuale accelerazione cosmica)”, ha spiegato Livio. “Il lato sinistro descrive la geometria dello spazio-tempo. L’uguaglianza riflette il fatto che nella relatività generale di Einstein, la massa e l’energia determinano la geometria e contemporaneamente la curvatura, che è una manifestazione di ciò che chiamiamo gravità.”

” È un’equazione molto elegante”, ha detto Kyle Cranmer, fisico della New York University, aggiungendo che l’equazione rivela la relazione tra spazio-tempo e materia ed energia. “Questa equazione ti dice come sono correlati-come la presenza del sole deforma lo spazio-tempo in modo che la Terra si muova attorno ad essa in orbita, ecc. Ti dice anche come l’universo si è evoluto dal Big Bang e prevede che ci dovrebbero essere buchi neri.”

Il modello standard

Un’altra delle teorie regnanti della fisica, il modello standard descrive la raccolta di particelle fondamentali che attualmente si pensa costituiscano il nostro universo.

La teoria può essere incapsulata in un’equazione principale chiamata modello standard Lagrangiana (dal nome del matematico e astronomo francese del xviii secolo Joseph Louis Lagrange), che è stata scelta dal fisico teorico Lance Dixon dello SLAC National Accelerator Laboratory in California come sua formula preferita.

“Ha descritto con successo tutte le particelle elementari e le forze che abbiamo osservato in laboratorio fino ad oggi — tranne la gravità”, ha detto Dixon a LiveScience. “Questo include, ovviamente, il bosone di Higgs(come) scoperto di recente, phi nella formula. È completamente auto-coerente con la meccanica quantistica e la relatività speciale.”

La teoria del modello standard non è ancora stata unita alla relatività generale, motivo per cui non può descrivere la gravità.

Calcolo

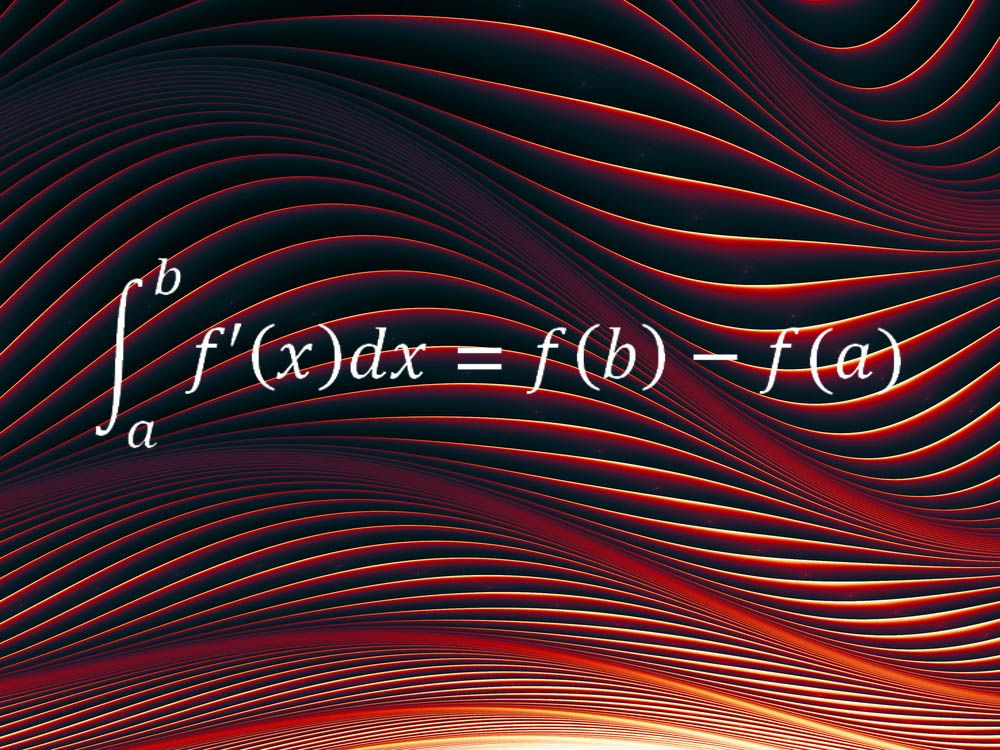
Mentre le prime due equazioni descrivono aspetti particolari del nostro universo, un’altra equazione preferita può essere applicata a tutti i tipi di situazioni. Il teorema fondamentale del calcolo costituisce la spina dorsale del metodo matematico noto come calcolo e collega le sue due idee principali, il concetto di integrale e il concetto di derivato.

” In parole semplici, dice che il cambiamento netto di una quantità liscia e continua, come una distanza percorsa, su un dato intervallo di tempo (cioè la differenza nei valori della quantità nei punti finali dell’intervallo di tempo) è uguale all’integrale del tasso di variazione di quella quantità, cioè l’integrale della velocità”, ha detto Melkana Brakalova-Trevithick, presidente del dipartimento di matematica della Fordham University, che ha scelto questa equazione come sua preferita. “Il teorema fondamentale del calcolo (FTC) ci consente di determinare la variazione netta su un intervallo in base alla velocità di variazione sull’intero intervallo.”

I semi del calcolo iniziarono in tempi antichi, ma gran parte di esso fu messo insieme nel 17 ° secolo da Isaac Newton, che usò il calcolo per descrivere i moti dei pianeti attorno al sole.

Teorema di Pitagora

Un’equazione “vecchia ma buona” è il famoso teorema di Pitagora, che ogni studente di geometria iniziale impara.

Questa formula descrive come, per qualsiasi triangolo rettangolo, il quadrato della lunghezza dell’ipotenusa, c, (il lato più lungo di un triangolo rettangolo) è uguale alla somma dei quadrati delle lunghezze degli altri due lati (a e b). Quindi, a^2 + b^2 = c^2

“Il primo fatto matematico che mi ha stupito è stato il teorema di Pitagora”, ha detto la matematica Daina Taimina della Cornell University. “Ero un bambino allora e mi sembrava così incredibile che funziona in geometria e funziona con i numeri!”

1 = 0,999999999….

Questa semplice equazione, in cui si afferma che la quantità 0.999, seguito da un infinito stringa di nove, è equivalente a uno, è il preferito di matematico Steven Strogatz della Cornell University.

“Mi piace quanto sia semplice — tutti capiscono cosa dice — ma quanto sia provocatorio”, ha detto Strogatz. “Molte persone non credono che potrebbe essere vero. È anche splendidamente equilibrato. Il lato sinistro rappresenta l’inizio della matematica; il lato destro rappresenta i misteri dell’infinito.”

la relatività Speciale

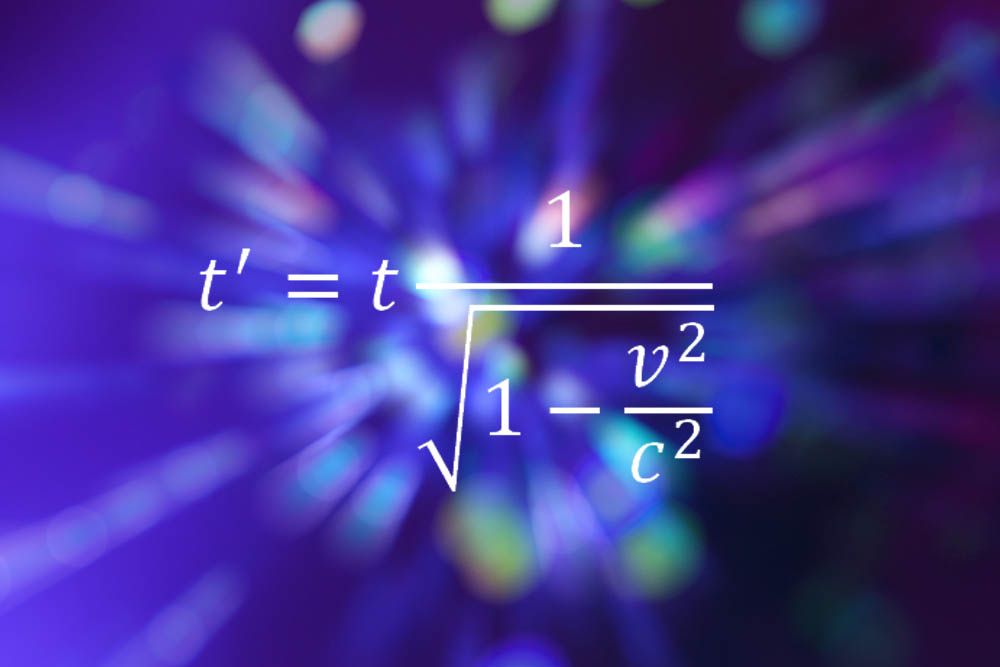
Einstein rende nuovamente l’elenco con le sue formule per la relatività speciale, che viene descritto come il tempo e lo spazio non sono concetti assoluti, ma sono piuttosto relativa, a seconda della velocità dell’osservatore. L’equazione sopra mostra come il tempo si dilata o rallenta, più velocemente una persona si muove in qualsiasi direzione.

“Il punto è che è davvero molto semplice”, ha detto Bill Murray, un fisico delle particelle presso il laboratorio del CERN di Ginevra. “Non c’è nulla che uno studente di livello A non possa fare, nessuna derivata complessa e algebre di traccia. Ma ciò che incarna è un modo completamente nuovo di guardare il mondo, un intero atteggiamento verso la realtà e la nostra relazione con essa. Improvvisamente, il rigido cosmo immutabile viene spazzato via e sostituito con un mondo personale, legato a ciò che osservi. Ci si sposta dall’essere al di fuori dell’universo, guardando in basso, a uno dei componenti al suo interno. Ma i concetti e la matematica possono essere afferrati da chiunque voglia.”

Murray ha detto che preferiva le equazioni della relatività speciale alle formule più complicate della teoria successiva di Einstein. “Non potrei mai seguire la matematica della relatività generale”, ha detto.

Equazione di Eulero

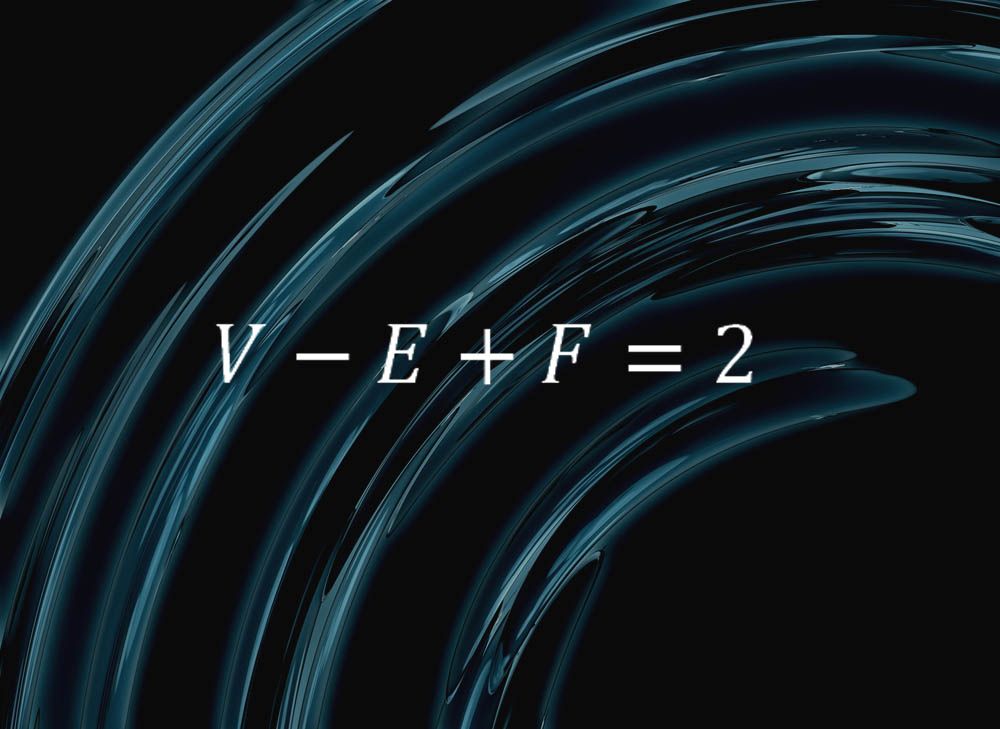
Questa semplice formula incapsula qualcosa di puro nella natura delle sfere:

“Dice che se tagli la superficie di una sfera in facce, bordi e vertici, e lascia che F sia il numero di facce, E il numero di bordi e V il numero di vertici, otterrai sempre V – E + F = 2”, ha detto Colin Adams, matematico del Williams College nel Massachusetts.

“Quindi, ad esempio, prendi un tetraedro, composto da quattro triangoli, sei bordi e quattro vertici”, ha spiegato Adams. “Se soffi forte in un tetraedro con facce flessibili, potresti arrotondarlo in una sfera, quindi in questo senso, una sfera può essere tagliata in quattro facce, sei bordi e quattro vertici. E vediamo che V – E + F = 2. Lo stesso vale per una piramide con cinque facce-quattro triangolari e un quadrato – otto bordi e cinque vertici ” e qualsiasi altra combinazione di facce, bordi e vertici.

“Un fatto molto interessante! La combinatoria dei vertici, dei bordi e delle facce sta catturando qualcosa di molto fondamentale sulla forma di una sfera”, ha detto Adams.

Equazioni di Eulero-Lagrange e teorema di Noether

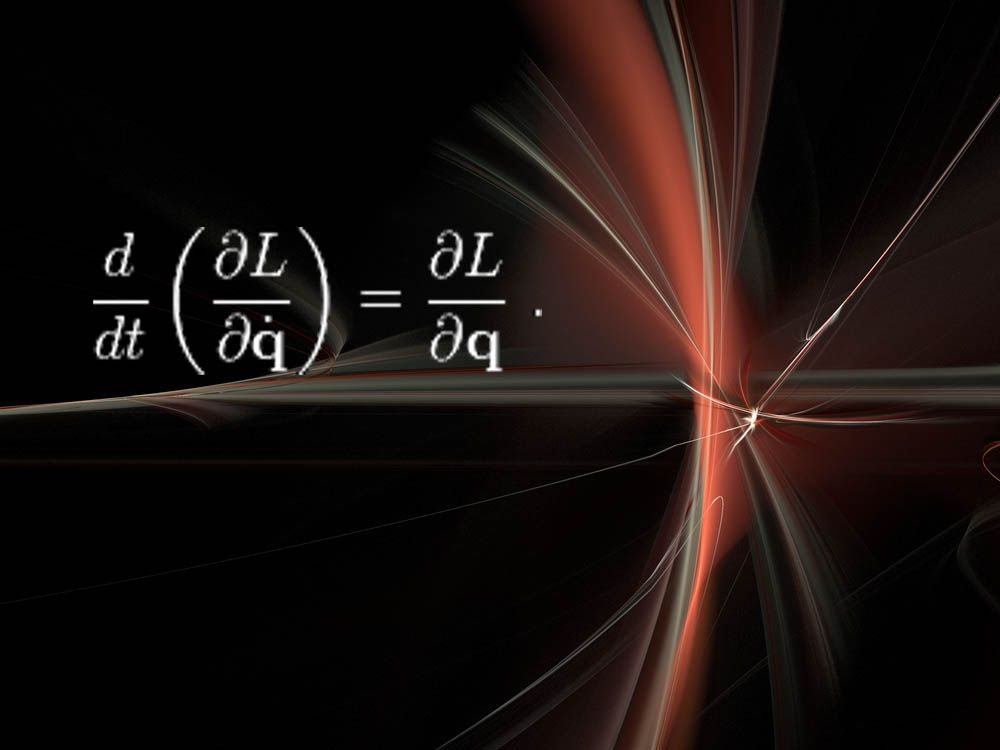
“Questi sono piuttosto astratti, ma incredibilmente potenti”, ha detto Cranmer della NYU. “La cosa bella è che questo modo di pensare alla fisica è sopravvissuto ad alcune importanti rivoluzioni in fisica, come la meccanica quantistica, la relatività, ecc.”

Qui, L sta per Lagrangiana, che è una misura di energia in un sistema fisico, come molle, leve o particelle fondamentali. “Risolvere questa equazione ti dice come il sistema si evolverà nel tempo”, ha detto Cranmer.

Uno spinoff dell’equazione lagrangiana è chiamato teorema di Noether, dopo il matematico tedesco del 20 ° secolo Emmy Noether. “Questo teorema è davvero fondamentale per la fisica e il ruolo della simmetria”, ha detto Cranmer. “Informalmente, il teorema è che se il tuo sistema ha una simmetria, allora c’è una legge di conservazione corrispondente. Ad esempio, l’idea che le leggi fondamentali della fisica siano le stesse oggi come domani (simmetria temporale) implica che l’energia sia conservata. L’idea che le leggi della fisica siano le stesse qui come sono nello spazio esterno implica che lo slancio sia conservato. La simmetria è forse il concetto guida nella fisica fondamentale, principalmente a causa del contributo.”

La Callan-Symanzik equazione

“Callan-Symanzik equazione è vitale principi della prima equazione, dal 1970, essenziale, per descrivere come ingenue aspettative non riuscirà in un mondo quantistico”, ha detto il fisico teorico Matt Strassler della Rutgers University.

L’equazione ha numerose applicazioni, tra cui consentendo ai fisici di stimare la massa e le dimensioni del protone e del neutrone, che costituiscono i nuclei degli atomi.

La fisica di base ci dice che la forza gravitazionale, e la forza elettrica, tra due oggetti è proporzionale all’inverso della distanza tra loro al quadrato. Ad un livello semplice, lo stesso vale per la forza nucleare forte che lega protoni e neutroni insieme per formare i nuclei degli atomi e che lega i quark insieme per formare protoni e neutroni. Tuttavia, minuscole fluttuazioni quantistiche possono alterare leggermente la dipendenza di una forza dalla distanza, il che ha conseguenze drammatiche per la forte forza nucleare.

“Impedisce a questa forza di diminuire a lunghe distanze e la fa intrappolare i quark e combinarli per formare i protoni e i neutroni del nostro mondo”, ha detto Strassler. “Ciò che l’equazione di Callan-Symanzik fa è mettere in relazione questo effetto drammatico e difficile da calcolare, importante quando è approssimativamente la dimensione di un protone, con effetti più sottili ma più facili da calcolare che possono essere misurati quando è molto più piccolo di un protone.”

La superficie minima equazione

“La superficie minima equazione in qualche modo di codificare le belle pellicole di sapone che si forma sul filo dei confini quando si immergeteli in acqua saponata,”ha detto matematico Frank Morgan del Williams College. “Il fatto che l’equazione sia ‘non lineare’, che coinvolge poteri e prodotti di derivati, è il suggerimento matematico codificato per il comportamento sorprendente delle pellicole di sapone. Questo è in contrasto con le equazioni differenziali alle derivate parziali lineari più familiari, come l’equazione del calore, l’equazione delle onde e l’equazione di Schrödinger della fisica quantistica.”