Integrali definiti
Ti piacerebbe leggere prima Introduzione all’integrazione!
Integrazione
|
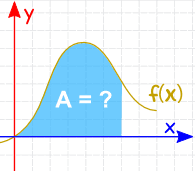
L’integrazione può essere utilizzata per trovare aree, volumi, punti centrali e molte cose utili. Ma è spesso utilizzato per trovare l’area sotto il grafico di una funzione come questa: |
 |
|
|
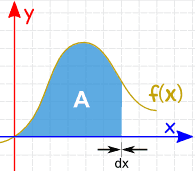
L’area può essere trovato con l’aggiunta di fette di che approccio zero in larghezza: E ci sono delle Regole di Integrazione che ci aiutano a ottenere la risposta. |
 |
la Notazione
Il simbolo per “Integrale” è un elegante “S” (per “Somma”, l’idea della somma di fette):
Dopo l’Integrale Simbolo abbiamo messo la funzione che si desidera trovare l’integrale della (chiamato Integrand).
E poi finire con dx per significare che le fette vanno nella direzione x (e si avvicinano allo zero in larghezza).
Integrale definito
Un Integrale definito ha valori iniziali e finali: in altre parole c’è un intervallo .
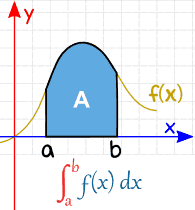
a e b (chiamati limiti, limiti o limiti) sono messi in basso e in alto della “S”, in questo modo:
 |
 |
|
| Definite Integral (from a to b) |
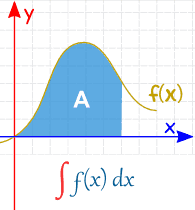
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
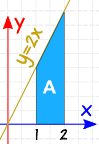
Esempio: Cos’è 2 ∫ 1 2x dx
Ci viene chiesto l’Integrale Definito, da 1 a 2, di 2x dx
Per prima cosa dobbiamo trovare l’Integrale Indefinito.
Usando le Regole di Integrazione troviamo che ∫2x dx = x2 + C
Ora calcoliamo che a 1, e 2:
- A x=1: ∫2x dx = 12 + C
- A x=2: ∫2x dx = 22 + C
Sottrarre:
E “C” viene annullato … quindi, con Integrali Definiti possiamo ignorare C.
Risultato:

Controllare: con una forma semplice, andiamo a provare anche il calcolo dell’area geometrica:
Un = 2+42 × 1 = 3
Sì, ha un’area di 3.
(Evviva!)
Notazione: Siamo in grado di mostrare l’integrale indefinito (senza +C) all’interno delle parentesi quadre, con i limiti a e b, come questo:
Esempio (continua)
Un buon modo per mostrare la tua risposta:
=
proviamo un altro esempio:
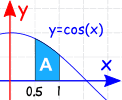
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
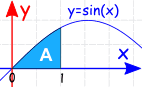
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
L’Integrale Indefinito è: ∫sin(x) dx = −cos(x) + C
Dal momento che stiamo andando da 0, possiamo calcolare l’integrale x=1?
−cos (1) = -0.540…
Cosa? È negativo? Ma sembra positivo nel grafico.
Bene … abbiamo fatto un errore!
Perché abbiamo bisogno di sottrarre l’integrale a x = 0. Non dovremmo supporre che sia zero.
Quindi facciamolo correttamente, sottraendo l’uno dall’altro:
=
Che è meglio!
Ma possiamo avere regioni negative, quando la curva è sotto l’asse:

Esempio:
L’Integrale Definito, da 1 a 3, di cos(x) dx:
si Noti che alcuni di esso è positivo, a volte negativo.
L’integrale definito calcolerà il valore netto.
Facciamo i calcoli:
=
Jump c’è più negativo che positivo con il risultato netto di -0.700….
quindi abbiamo questa cosa importante da ricordare:
Prova a integrare cos(x) con diversi valori iniziali e finali per vedere di persona come funzionano i positivi e i negativi.
Area positiva
Ma a volte vogliamo che tutta l’area sia trattata come positiva (senza che la parte sotto l’asse venga sottratta).
In questo caso dobbiamo calcolare le aree separatamente, come in questo esempio:

Esempio: Qual è l’area totale tra y = cos (x) e l’asse x, da x = 1 a x = 3?
Questo è come l’esempio che abbiamo appena fatto, ma ora ci aspettiamo che tutta l’area sia positiva (immagina di doverla dipingere).
ora dobbiamo fare i pezzi separatamente:
- Uno per l’area sopra l’asse x
- Uno per l’area al di sotto dell’asse x
La curva interseca l’asse x in x = π/2 si ha:
Da 1 a π/2:
= sin(π/2) − sin(1)
Da π/2 3:
= sin(3) − sin(π/2)
Quest’ultimo esce negativo, ma vogliamo che sia positivo, quindi:
Area totale = 0.159… + 0.859… = 1.018…
Questo è molto diverso dalla risposta nell’esempio precedente.
Continuo
Oh sì, la funzione che stiamo integrando deve essere Continua tra a e b: nessun buco, salti o asintoti verticali (dove la funzione si dirige verso l’alto / verso il basso verso l’infinito).
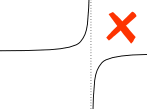
Esempio:
Un asintoto verticale tra a e b influisce sull’integrale definito.
Proprietà
Area sopra-area sotto
L’integrale aggiunge l’area sopra l’asse ma sottrae l’area sotto, per un”valore netto”:
l’Aggiunta di Funzioni
L’integrale di f+g è uguale all’integrale di f plus l’integrale di g:
Invertendo l’intervallo
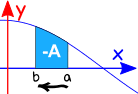
Invertire la direzione dell’intervallo dà il negativo della direzione originale.
![]()

Leave a Reply