Articles

Facile Permutazioni e combinazioni

by admin

Ho sempre confuso “permutazione” e “combinazione” – quale è quale?

Ecco un modo semplice per ricordare: la permutazione sembra complicata, vero? E lo e’. Con le permutazioni, ogni piccolo dettaglio è importante. Alice, Bob e Charlie è diverso da Charlie, Bob e Alice (inserisci i nomi dei tuoi amici qui).

Combinazioni, d’altra parte, sono abbastanza facile andare. I dettagli non contano. Alice, Bob e Charlie è lo stesso di Charlie, Bob e Alice.

Le permutazioni sono per gli elenchi (l’ordine conta) e le combinazioni sono per i gruppi (l’ordine non importa).

Sai, un” lucchetto a combinazione “dovrebbe davvero essere chiamato”blocco di permutazione”. L’ordine si mette i numeri in materia.

Permutazioni e combinazioni facili

Un vero “blocco a combinazione” accetterebbe sia 10-17-23 che 23-17-10 come corretti.

Permutazioni: I dettagli pelosi

Iniziamo con le permutazioni, o tutti i possibili modi di fare qualcosa. Stiamo usando il termine fancy-pants “permutazione”, quindi ci occuperemo di ogni dettaglio, incluso l’ordine di ogni articolo. Diciamo che abbiamo 8 persone:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

In quanti modi possiamo assegnare un premio di 1°, 2 ° e 3 ° posto tra otto concorrenti? (Oro / Argento / bronzo)

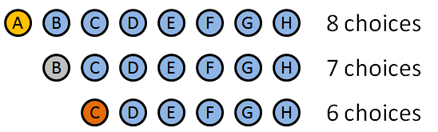
permuation esempio medaglie

Useremo permutazioni poiché l’ordine in cui distribuiamo queste medaglie è importante. Ecco come si rompe:

  • Medaglia d’oro: 8 scelte: A B C D E F G H (Intelligente come ho fatto i nomi corrispondono con le lettere, eh?). Diciamo che A vince l’oro.
  • Medaglia d’argento: 7 scelte: B C D E F G H. Diciamo che B vince l’argento.
  • Medaglia di bronzo: 6 scelte: C D E F G H. Diciamo… C vince il bronzo.

Abbiamo scelto alcune persone per vincere, ma i dettagli non contano: abbiamo avuto 8 scelte all’inizio, poi 7, poi 6. Il numero totale di opzioni era $8 * 7 * 6 = 336$.

Diamo un’occhiata ai dettagli. Abbiamo dovuto ordinare 3 persone su 8. Per fare questo, abbiamo iniziato con tutte le opzioni (8) poi le abbiamo portate via una alla volta (7, poi 6) fino a quando non abbiamo finito le medaglie.

Sappiamo che il fattoriale è:

\ displaystyle{ 8! = 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1}

Sfortunatamente, questo fa troppo! Noi vogliamo solo $8 * 7 * 6$. Come possiamo “fermare” il fattoriale a 5?

Questo è dove le permutazioni si raffreddano: nota come vogliamo sbarazzarci di $5 * 4 * 3 * 2 * 1$. Qual è un altro nome per questo? 5 fattoriale!

Quindi, se facciamo 8!/5! abbiamo ottenuto:

\displaystyle{\frac{8!}{5!} = \ frac{8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1}{5 \cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} = 8 \ cdot 7 \ cdot 6}

E perché abbiamo usato il numero 5? Perché è stato lasciato dopo che abbiamo scelto 3 medaglie da 8. Quindi, un modo migliore per scrivere questo sarebbe:

\displaystyle{\frac{8!}{(8-3)!}}

dove 8!/(8-3)! è solo un modo elegante di dire ” Usa i primi 3 numeri di 8!”. Se abbiamo n elementi totali e vogliamo scegliere k in un certo ordine, otteniamo:

\displaystyle {\frac{n!(n-k)!}}

E questa è la formula di permutazione fantasia: Hai n elementi e vuoi trovare il numero di modi in cui k elementi possono essere ordinati:

\displaystyle{P(n,k) = \frac{n!(n-k)!}}

Combinazioni, Ho!

Le combinazioni sono facili. L’ordine non ha importanza. Si può mescolare e sembra lo stesso. Diciamo che sono un tirchio e non posso permettermi medaglie d’oro, d’argento e di bronzo separate. In realtà, posso permettermi solo lattine vuote.

In quanti modi posso dare 3 lattine a 8 persone?

Bene, in questo caso, l’ordine in cui scegliamo le persone non ha importanza. Se do una lattina ad Alice, Bob e poi Charlie, e ‘ come dare a Charlie, Alice e poi Bob. In entrambi i casi, sono ugualmente delusi.

Questo solleva un punto interessante — abbiamo alcune ridondanze qui. Il suo nome deriva dal nome del personaggio. Per un momento, cerchiamo solo di capire quanti modi possiamo riorganizzare 3 persone.

Bene, abbiamo 3 scelte per la prima persona, 2 per la seconda e solo 1 per l’ultima. Quindi abbiamo $3 * 2 * 1$ modi per riorganizzare 3 persone.

Aspetta un minuto… sembra un po ‘ una permutazione! Mi hai ingannato!

In effetti l’ho fatto. Se hai N persone e vuoi sapere quanti accordi ci sono per tutti loro, è solo N fattoriale o N!

Quindi, se abbiamo 3 lattine da regalare, ce ne sono 3! o 6 varianti per ogni scelta che scegliamo. Se vogliamo capire quante combinazioni abbiamo, creiamo solo tutte le permutazioni e dividiamo per tutte le ridondanze. Nel nostro caso, otteniamo 336 permutazioni (dall’alto), e dividiamo per le 6 ridondanze per ogni permutazione e otteniamo 336/6 = 56.

La formula generale è

\displaystyle{C(n,k) = \frac{P(n,k)}{k!}}

che significa “Trova tutti i modi per scegliere k persone da n e dividi per k! variante”. Scrivendo questo, otteniamo la nostra formula di combinazione, o il numero di modi per combinare k elementi da un insieme di n:

\displaystyle{C(n,k) = \frac{n!(n-k)!k!}}

A volte C(n,k) è scritto come:

\displaystyle{\binom {n}{k}}

che è il coefficiente binomiale.

Alcuni esempi

Ecco alcuni esempi di combinazioni (l’ordine non importa) dalle permutazioni (l’ordine conta).

  • Combinazione: Scegliere un team di 3 persone da un gruppo di 10. C C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    Permutazione: scegliere un presidente, VP e Waterboy da un gruppo di 10. P P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • Combinazione: scegliere 3 dessert da un menu di 10. C(10,3) = 120.

    Permutazione: Elencando i tuoi 3 dessert preferiti, in ordine, da un menu di 10. P(10,3) = 720.

Non memorizzare le formule, capire perché funzionano. Le combinazioni suonano più semplici delle permutazioni e lo sono. Hai meno combinazioni di permutazioni.

Altri post di questa serie

  1. Facili permutazioni e combinazioni
  2. Naviga in una griglia usando combinazioni e permutazioni
  3. Come capire le combinazioni usando la moltiplicazione
  4. Perché moltiplichiamo le combinazioni?