Da Jason McCormick
Professore Associato, Civile & Ingegneria Ambientale, Università del Michigan, Ann Arbor, MI, USA

Momento connessioni di forma rettangolare e quadrata cava sezioni strutturali (HSS) hanno ricevuto minore considerazione rispetto ad HSS-di-HSS connessioni composto caricato assialmente membri (T, Y, croce-e K-connessioni). La maggior parte degli studi statici incentrati su queste connessioni hanno preso in considerazione i sistemi a traliccio Vierendeel. Questi sistemi sono spesso formati da accordi quadrati o rettangolari superiore e inferiore che sono collegati con quadrati o rettangolari web verticale (ramo) membri (Figura 1). Come risultato di questa configurazione, la connessione chord-to-web subisce una significativa flessione insieme a carichi di taglio e assiali e non è considerata una connessione bloccata come avviene comunemente nei tipici sistemi a traliccio. Originariamente concepito nel 1896 da Arthur Vierendeel, non è stato fino HSS sono stati sviluppati che il potenziale per capriate Vierendeel iniziato a essere realizzato (Korol et al. 1977), ma il loro uso richiedeva una comprensione di come trasferire il momento tra le connessioni T HSS-to-HSS.

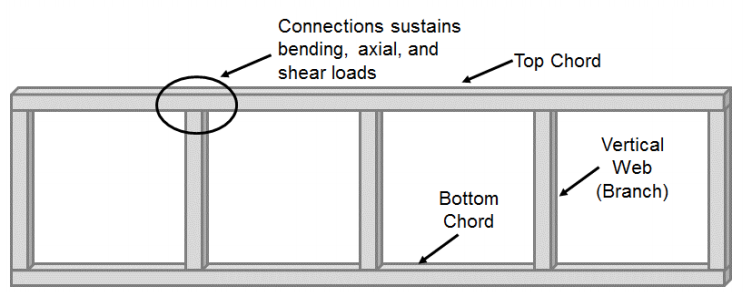
Molti dei primi studi di queste connessioni si sono concentrati sulla capacità della connessione di sviluppare la capacità di momento completo del membro del ramo. Jubb e Redwood (1966) hanno mostrato che quando la sezione di ramo aveva una larghezza uguale alla sezione di corda (β=1) la capacità del momento completo del membro HSS poteva essere raggiunta senza rinforzo. Tuttavia, questo studio non ha considerato la potenziale perdita di capacità di momento dovuta alla presenza di carico assiale. D’altra parte, Korol et al. (1977) ha dimostrato che le connessioni con una larghezza del ramo inferiore rispetto alla corda non potevano sviluppare la capacità del momento completo del ramo senza rinforzare attraverso una serie di 29 diversi test di connessione considerando 5 diverse configurazioni (non rinforzate, piastre di rinforzo della flangia del ramo, rinforzi della flangia della corda, haunch e piramide troncata). In generale, la resistenza e la rigidità delle connessioni di tipo Vierendeel non rinforzate diminuiscono con un aumento del rapporto di snellezza della corda (B/t) e una diminuzione del rapporto larghezza ramo-corda (β). Di conseguenza, le connessioni di tipo truss Vierendeel non differenziate possono essere considerate rigide (cioè subiscono una rotazione relativa minima tra l’accordo e il ramo) solo quando il rapporto di larghezza tra ramo e accordo è 1.0 e il rapporto di snellezza dell’accordo è basso o la connessione è rinforzata (Packer 1993).

Poiché i momenti massimi in questi giunti possono verificarsi a deformazioni eccessivamente grandi, viene adottato un approccio simile a quello utilizzato per giunti HSS quadrati e rettangolari caricati assialmente, dove per una capacità portante finale o un limite di deformazione o rotazione viene utilizzato per caratterizzare il momento di progettazione (Wardenier 1982). AISC 360-10 (capitolo K3) considera tre stati limite per le connessioni HSS T quadrate e rettangolari in flessione statica in piano: plastificazione della parete della corda, cedimento locale della parete laterale e resa locale del ramo a causa della distribuzione irregolare del carico. La plastificazione della parete dell’accordo si verifica a causa della larghezza del membro del ramo inferiore alla larghezza dell’accordo (β ≤ 0,85) che richiede che i carichi di tensione e compressione prodotti dal momento flettente vengano trasferiti attraverso la faccia relativamente flessibile dell’accordo piuttosto che direttamente alle pareti laterali più rigide. L’equazione dello stato limite (Equazione AISC 360-10 K3-6) può essere derivata dalla teoria della linea di snervamento (Figura 2):

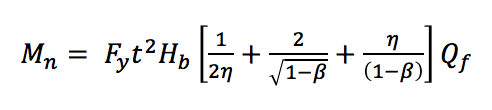
Mn è il momento nominale potenza di connessione, l’Esercizio è specificato il limite di snervamento minimo dell’accordo, Hb è l’altezza complessiva del ramo, h è il carico parametro di lunghezza pari all’altezza della diramazione divisa per la larghezza della corda, assumendo un 90o angolo tra la corda e membro del ramo, come è tipico di Vierendeel capriate)e Qf è un parametro per ridurre la capacità del comune in presenza di compressione assiale dell’accordo.

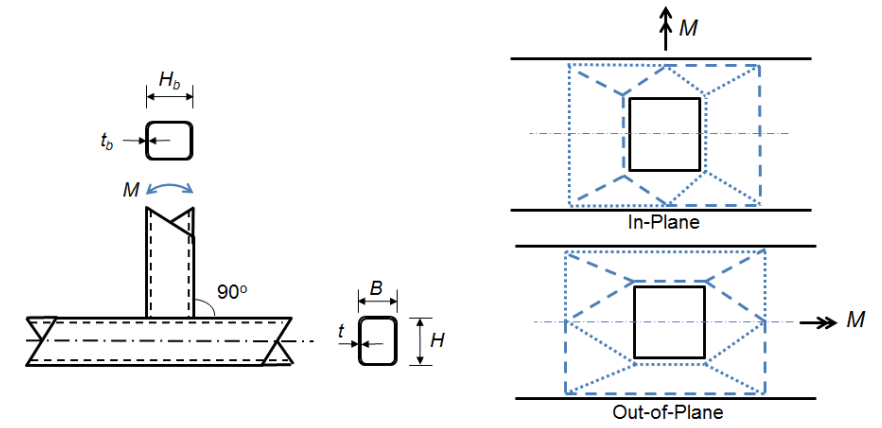
Gli altri due stati limite sono associati con connessioni in cui la larghezza del ramo membro è uguale o quasi uguale alla larghezza dell’accordo (β > 0.85) significa che i carichi di tensione e compressione sviluppati nelle flange del membro del ramo vengono trasferiti quasi direttamente nelle pareti laterali più rigide della corda. Lo stato limite per il rendimento locale del muro laterale (Equazione AISC 360-10 K3-7) di una connessione a T può quindi essere derivato dall’equazione di rendimento locale del web per forze concentrate applicate a una distanza dall’estremità del membro maggiore della sua profondità (Equazione AISC 360-10 J10-2):

Mn = 0.5Fyt(Hb + 5t)2
Equazione di 2

Per i locali di cedere il ramo a causa della distribuzione non omogenea del carico (AISC 360-10 Equazione K3-8) in un raccordo a T, una larghezza efficace approccio è utilizzato per ridurre la capacità del rinforzo membro per ottenere il momento nominale applicato dalla brace:

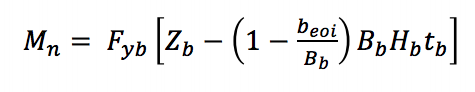
Fyb è il limite minimo di snervamento specificato del ramo, Zb è il modulo di sezione plastica del ramo sull’asse di piegatura, beoi è la larghezza effettiva del ramo, Bb è la larghezza complessiva del ramo e tb è lo spessore della parete di progettazione del ramo.

Poiché esistono prove sperimentali limitate a supporto di modelli di progettazione specifici per le connessioni a traliccio Vierendeel (connessioni a T) in flessione fuori piano, vengono utilizzati stati limite analoghi a quelli per la piegatura in piano (Packer et al. 2010). Un ulteriore stato limite di errore distorsivo della corda si sviluppa dalla coppia applicata alla corda dal membro del ramo come risultato del momento fuori piano. Questa coppia può portare alla distorsione romboidale dell’accordo. Le equazioni del momento nominale per la piegatura fuori piano possono essere trovate nelle equazioni AISC 360-10 K3-9, K3-10, K3-11 e K3-12. Le equazioni per la flessione sia in piano che fuori piano delle connessioni a T sono simili a quelle adottate a livello internazionale (Packer et al. 2010).

Le equazioni di progetto di cui sopra sono state derivate considerando i sistemi a traliccio Vierendeel sotto carichi statici. Uno studio recente (Fadden et al. 2015) ha promosso questo lavoro per considerare il comportamento delle connessioni momento HSS-HSS quadrate e rettangolari sotto grandi carichi ciclici per l’uso in sistemi di frame momento sismico basati su tubi (frame momento intermedio e speciale). Tale sistema cerca di sfruttare le eccellenti proprietà assiali, di piegatura e torsionali, l’elevato rapporto resistenza-peso e la natura architettonicamente piacevole dell’HSS quadrato e rettangolare. L’elevata resistenza torsionale può portare ad una riduzione del rinforzo laterale del fascio mentre l’elevato rapporto resistenza / peso si traduce in una massa sismica inferiore. Tuttavia, tali collegamenti devono potere subire l’incernieramento di plastica stabile dell’elemento del fascio in cui 80% della capacità di plastica dell’elemento del fascio è mantenuto a 0,2 rad. (FMI) o 0.4 rad. (SMF) di inter-story drift (AISC 341-10). Dato che l’attuale progettazione sismica dei sistemi moment frame richiede che la maggior parte del comportamento anelastico si verifichi nel membro del fascio, il membro del fascio deve anche raggiungere la sua piena capacità plastica prima di subire l’instabilità locale. Fadden e McCormick (2014a) hanno considerato sia modelli sperimentali che ad elementi finiti per determinare i requisiti di larghezza-spessore e profondità-spessore limitanti per HSS in flessione poiché quelli specificati nelle attuali disposizioni sismiche AISC (AISC 341-10) sono stati in gran parte sviluppati sulla base di test di membri HSS caricati assialmente ciclici.

Per determinare la configurazione e i requisiti di dettaglio appropriati per soddisfare questa domanda di resistenza e duttilità, sono state testate sperimentalmente quattro diverse configurazioni di connessione: due connessioni non rinforzate saldate direttamente (ineguagliabili e abbinate) e due connessioni rinforzate (piastra passante e piastra a membrana esterna). Tutte le connessioni utilizzavano una colonna HSS 10x10x5 / 8. Le connessioni saldate direttamente utilizzavano saldature CJP prequalificate come specificato in AWS D1.1 (2010). Per la connessione ineguagliata, il raggio era un HSS 12x8x3 / 8 (β = 0.8) suggerendo che la plastificazione della faccia della colonna può essere una preoccupazione. Per il collegamento abbinato, il fascio era un HSS 12x10x3 / 8 (β = 1.0) permettendo che i carichi fossero trasferiti direttamente nella parete laterale. È stato utilizzato il protocollo di caricamento AISC per la prequalificazione delle connessioni momento sismico (AISC 341-10) per caricare le connessioni. Il comportamento delle connessioni era come previsto con la connessione ineguagliata che mostrava deformazioni sulla faccia della colonna, mentre la connessione abbinata era in grado di trasferire il carico sulle pareti laterali della colonna. Tuttavia, entrambe le connessioni non sono riuscite a causa della frattura nel metallo base della colonna alla punta dell’angolo della saldatura (Figura 3). Questo guasto fragile a rotazioni di 0,4 rad. e 0,5 rad., rispettivamente, ha confermato che le connessioni saldate direttamente non forniscono il comportamento appropriato per le applicazioni sismiche.

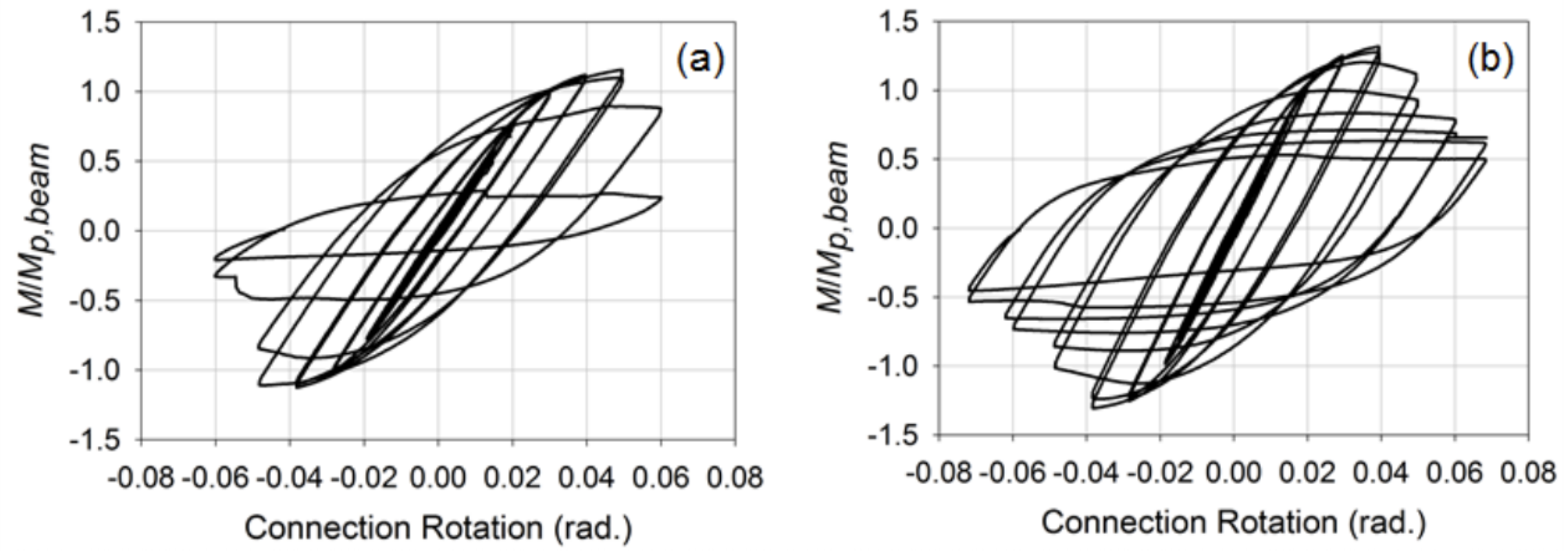
Il rafforzamento delle connessioni sono poi stati sviluppati considerando attraverso la piastra e la membrana esterna piatti che vengono spesso utilizzati in un’ampia flangia della trave-HSS colonna connessioni in modo da fornire un meccanismo migliore per trasferire la tensione e forze di compressione per il fianco della colonna e ridurre le concentrazioni di pressione posizionati sulle saldature. Per queste connessioni, le travi erano membri HSS 12x8x3/8 (β = 0,8). Informazioni relative alla procedura specifica utilizzata per progettare e dettagliare queste connessioni possono essere trovate in Fadden e McCormick (2014b) e Fadden et al. (2015). Posti sotto lo stesso carico delle connessioni non rinforzate, le connessioni hanno mostrato un comportamento più stabile con la cerniera in plastica che si trovava lontano dalla faccia della colonna all’estremità della piastra del diaframma passante o esterno (Figura 4). Entrambe le connessioni sono state anche in grado di raggiungere 0.4 rad. di rotazione prima di subire instabilità locale che ha provocato il degrado della capacità momento. Tuttavia, la frattura ha iniziato all’angolo del fascio HSS a causa del ciclismo a grandi livelli di rotazione di 0,7 rad. Un confronto delle curve di rotazione del momento normalizzate per le connessioni della piastra del diaframma abbinate ed esterne può essere visto in Figura 5. Nel complesso, le connessioni rinforzate hanno mostrato una promessa per l’uso di sistemi di frame sismici HSS-to-HSS, ma è necessario più lavoro per spostare queste connessioni verso un’eventuale prequalificazione.

AISC. (2010). “Disposizioni antisismiche per edifici in acciaio strutturale”. ANSI / AISC 341-10. Istituto americano di costruzione in acciaio, Chicago, IL.

AISC. (2010). “Specifiche per costruzioni edili in acciaio”. ANSI / AISC 360-10. Istituto americano di costruzione in acciaio, Chicago, IL.

AWS. (2010). “Codice di saldatura strutturale”. ANSI / AWS D1.1, società americana della saldatura, Miami, FL.

Fadden, F. e McCormick, J. (2014a). “Finite Element Model of the Cyclic Bending Behavior of Hollow Structural Sections”. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. e McCormick, J. (2014b). “HSS-to-HSS Seismic Moment Connection Performance and Design”. Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D., e McCormick, J. (2015). “Cyclic Testing of Welded HSS-to-HSS Moment Connections for Seismic Applications”. ASCE Journal of Structural Engineering, 141(2), 04014109-1-14.

Jubb, JEM e Redwood, RG (1966). “Progettazione di giunti a sezioni di scatola”” L’Institution of Structural Engineers, Conferenza sull’edilizia industrializzata e l’Ingegnere strutturale, Institute of Structural Engineers, Londra.

Korol, R. M., El-Zanaty, M., e Brady, F. J. (1977). “Connessioni larghezza disuguale di sezioni cave quadrate in capriate Vierendeel”” Canadian Journal of Civil Engineering, 4, 190-201.

Packer, J. A. (1993). “Connessioni momento tra sezioni cave rettangolari”” Journal of Constructional Steel Research, 25, 63-81.

Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G. J. e Kurobane, Y. (2010). Guida alla progettazione 3: Per giunti a sezione cava rettangolare (RHS) con carico prevalentemente statico 2a edizione. CIDECT, Canada.

Wardenier, J. (1982). “Giunti a sezione cava”. Delft University Press, Delft, Paesi Bassi.

Settembre 2016

Scarica il PDF