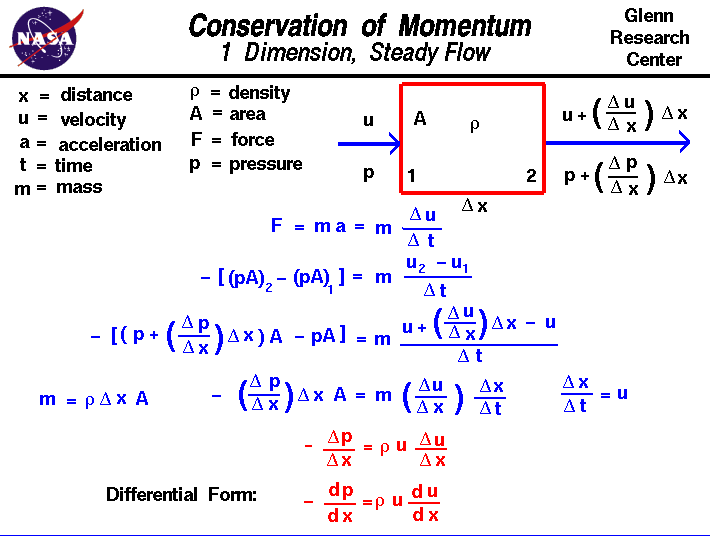
La conservazione della quantità di moto è un concetto fondamentale della fisicainsieme alla conservazione dell’energia e alla conservazione della massa.La quantità di moto è definita come la massa di un oggetto moltiplicata per la velocità dell’oggetto.La conservazione della quantità di moto afferma che, all’interno di un dominio problematico, la quantità di moto rimane costante;la quantità di moto non è né creata né distrutta, ma solo cambiataattraverso l’azione delle forze come descritto dalle leggi del moto di Newton.Trattare con la quantità di moto è più difficile che trattare con la massa e l’energia becausemomentum è avector quantityhaving sia una grandezza e una direzione. La quantità di moto è conservata in tutte e tredirezioni fisiche allo stesso tempo. È ancora più difficile quando si tratta di agasperché le forze in una direzione possono influenzare la quantità di moto in un’altra direzionea causa delle collisioni di molte molecole.In questa diapositiva, presenteremo un problema di flusso molto, molto semplificatodove le proprietà cambiano solo in una direzione.Il problema è ulteriormente semplificato considerando un flusso costante che non cambia nel tempo e limitando le forze solo a quelle associate thepressure.Be consapevoli che i problemi reali di flusso sono moltopiù complessi di questo semplice esempio.

Consideriamo il flusso di un gas attraverso un dominio in cui scorrono le proprietàcambiare solo in una direzione, che chiameremo “x”. Il gas entra nella stazione domainat 1 con una certa velocità u e una certa pressione pand esce alla stazione 2 con un valore diverso di velocità e pressione. Per semplicità, assumeremo che la densità r rimanga costante all’interno del domainand che anche l’area A attraverso la quale scorre il gas rimane costante. La posizione delle stazioni 1 e 2 sono separateda una distanza chiamata del x. (Delta è il piccolo triangolo sulla diapositivae è la lettera greca “d”. I matematici usano spesso questo simbolo per denotareun cambiamento o variazione di una quantità. Il carattere di stampa web non supportale lettere greche, quindi lo chiameremo semplicemente “del”.) Un cambiamento con la distanza è indicato come un gradientto evitare confusione con un cambiamento con il tempo che è chiamato un tasso.Il gradiente di velocità è indicato da del u / del x; il cambiamento di velocità percambio in distanza. Quindi alla stazione 2, la velocità è data dalla velocitàa 1 più il gradiente per la distanza.

Un’espressione simile dà la pressione all’uscita:

La seconda legge del moto di Newton afferma che la forza F è uguale alla variazione della quantità di moto rispetto al tempo. Per un oggetto con massa costante questo si riduce all’accelerazione dei tempi di massa a.An l’accelerazione è un cambiamento di velocità con un cambiamento nel tempo (del u / del t). Quindi:

La forza in questo problemaviene dal gradiente di pressione. Poiché la pressione è una forza per unità di area, la forza netta sul nostro dominio fluido è la pressione per l’area all’uscita meno la pressione per l’area all’ingresso.

Il segno meno all’inizio di questa espressione viene utilizzato perché i gas si spostano da una regione di alta pressione a una regione di bassa pressione; se la pressione aumenta withx, la velocità diminuirà. Sostituendo le nostre espressioni per velocitàe pressione:

Semplifica:

Notare che (del x / del t) è thevelocity e che la massa è la densità r volte il volume (zona tempi del x):

Semplificare:

I del p / del x e del u / del xrepresent la pressione e la velocità sfumature.Se vogliamo ridurre il nostro dominio giù differenziale dimensioni, questi gradienti di diventare differenziali:

Questo è un unidimensionale, costante forma ofEuler Equazione.È interessante notare che la pressione dropof un fluido (il termine a sinistra) è proporzionale sia al valore di thevelocity e il gradiente di velocità.Una soluzione di questa equazione della quantità di moto ci dà la forma delpressione dinamicache appare nell’equazione di Bernoulli.

Attività:
Visite guidate

• Equazioni di base della fluidodinamica:

Navigazione ..

Guida per principianti Home Page