Analisi di regressione lineare in Excel
Il tutorial spiega le basi dell’analisi di regressione e mostra alcuni modi diversi per eseguire la regressione lineare in Excel.
Immagina questo: ti vengono forniti molti dati diversi e ti viene chiesto di prevedere i numeri di vendita del prossimo anno per la tua azienda. Avete scoperto decine, forse anche centinaia, di fattori che possono eventualmente influenzare i numeri. Ma come fai a sapere quali sono veramente importanti? Eseguire l’analisi di regressione in Excel. Ti darà una risposta a questo e molte altre domande: Quali fattori contano e quali possono essere ignorati? Quanto strettamente sono questi fattori correlati tra loro? E quanto si può essere certi circa le previsioni?
- analisi di Regressione in Excel
- regressione Lineare in Excel con Strumenti di Analisi
- Disegnare una regressione lineare grafico
- analisi di Regressione in Excel con formule
l’analisi di Regressione in Excel – nozioni di base
la modellazione statistica, l’analisi di regressione è utilizzato per stimare le relazioni tra due o più variabili:
La variabile dipendente (aka criterion variable) è il fattore principale che stai cercando di capire e prevedere.
Le variabili indipendenti (ovvero variabili esplicative o predittori) sono i fattori che potrebbero influenzare la variabile dipendente.
L’analisi di regressione ti aiuta a capire come cambia la variabile dipendente quando varia una delle variabili indipendenti e consente di determinare matematicamente quale di queste variabili ha davvero un impatto.
Tecnicamente, un modello di analisi di regressione si basa sulla somma dei quadrati, che è un modo matematico per trovare la dispersione dei punti dati. L’obiettivo di un modello è quello di ottenere la somma più piccola possibile di quadrati e disegnare una linea che si avvicina di più ai dati.
In statistica, distinguono tra una regressione lineare semplice e multipla. La regressione lineare semplice modella la relazione tra una variabile dipendente e una variabile indipendente utilizzando una funzione lineare. Se si utilizzano due o più variabili esplicative per prevedere la variabile dipendente, si tratta di regressione lineare multipla. Se la variabile dipendente viene modellata come una funzione non lineare perché le relazioni di dati non seguono una linea retta, utilizzare invece la regressione non lineare. Il focus di questo tutorial sarà su una semplice regressione lineare.
Ad esempio, prendiamo i numeri di vendita per gli ombrelli degli ultimi 24 mesi e scopriamo le precipitazioni medie mensili per lo stesso periodo. Trama di questa informazioni su un grafico, e la linea di regressione, a dimostrare la relazione tra la variabile indipendente (la pioggia) e la variabile dipendente (ombrellone vendita):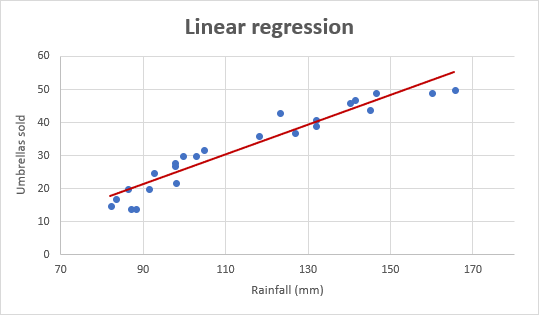
equazione di regressione Lineare
Matematicamente, una regressione lineare è definita dall’equazione:
in Cui:
- x è una variabile indipendente.
- y è una variabile dipendente.
- a è l’intercetta Y, che è il valore medio atteso di y quando tutte le variabili x sono uguali a 0. Su un grafico di regressione, è il punto in cui la linea attraversa l’asse Y.
- b è la pendenza di una linea di regressione, che è la velocità di variazione per y come x cambia.
- ε è il termine di errore casuale, che è la differenza tra il valore effettivo di una variabile dipendente e il suo valore previsto.
L’equazione di regressione lineare ha sempre un termine di errore perché, nella vita reale, i predittori non sono mai perfettamente precisi. Tuttavia, alcuni programmi, incluso Excel, eseguono il calcolo del termine di errore dietro le quinte. Così, in Excel, è possibile fare di regressione lineare utilizzando il metodo dei minimi quadrati e cerchi coefficienti a e b tali che:
Per esempio, l’equazione di regressione lineare assume la seguente forma:
Umbrellas sold = b * rainfall + a
esistono una manciata di modi diversi per trovare a e b. I tre metodi principali per eseguire l’analisi di regressione lineare in Excel sono:
- Strumento di regressione incluso con Analysis ToolPak
- Grafico a dispersione con una linea di tendenza
- Formula di regressione lineare
Di seguito troverai le istruzioni dettagliate sull’utilizzo di ciascun metodo.
Come eseguire la regressione lineare in Excel con Analysis ToolPak
Questo esempio mostra come eseguire la regressione in Excel utilizzando uno strumento speciale incluso nel componente aggiuntivo Analysis ToolPak.
Abilita il componente aggiuntivo Analysis ToolPak
Analysis ToolPak è disponibile in tutte le versioni di Excel dal 2019 al 2003 ma non è abilitato per impostazione predefinita. Quindi, è necessario accenderlo manualmente. Ecco come:
- Nel tuo Excel, fai clic su File> Opzioni.
- Nella finestra di dialogo Opzioni Excel, selezionare Componenti aggiuntivi nella barra laterale sinistra, assicurarsi che i componenti aggiuntivi di Excel siano selezionati nella casella Gestisci e fare clic su Vai.
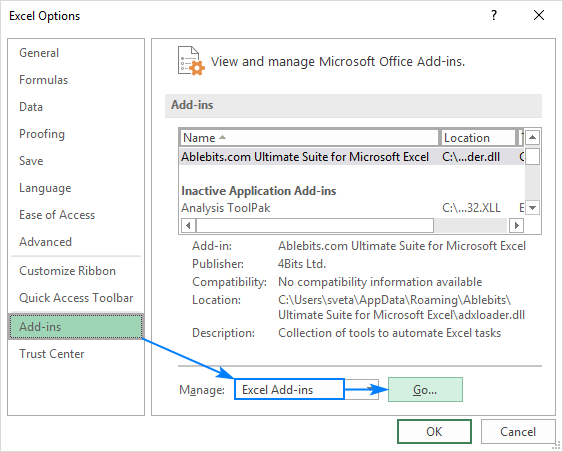
- Nella finestra di dialogo Componenti aggiuntivi, spuntare Analysis Toolpak e fare clic su OK:
Questo aggiungerà gli strumenti di analisi dei dati alla scheda Dati della barra multifunzione di Excel.
Esegui l’analisi di regressione
In questo esempio, faremo una semplice regressione lineare in Excel. Quello che abbiamo è un elenco delle precipitazioni medie mensili degli ultimi 24 mesi nella colonna B, che è la nostra variabile indipendente (predittore), e il numero di ombrelli venduti nella colonna C, che è la variabile dipendente. Naturalmente, ci sono molti altri fattori che possono influenzare le vendite, ma per ora ci concentriamo solo su queste due variabili: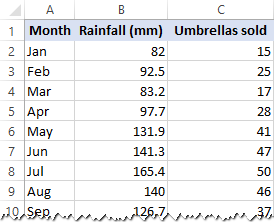
Con Strumenti di Analisi aggiunto abilitati, di effettuare la procedura per eseguire l’analisi di regressione in Excel:
- Nella scheda Dati, nell’Analisi di gruppo, fare clic su Analisi Dati di pulsante.
- Selezionare Regressione e fare clic su OK.
- Nella finestra di dialogo Regressione, configurare le seguenti impostazioni:
- Selezionare l’intervallo Y di input, che è la variabile dipendente. Nel nostro caso, si tratta di vendite di ombrelli (C1:C25).
- Seleziona l’intervallo X di input, cioè la tua variabile indipendente. In questo esempio, è la piovosità media mensile (B1:B25).
Se si sta costruendo un modello di regressione multipla, selezionare due o più colonne adiacenti con diverse variabili indipendenti.
- Seleziona la casella Etichette se ci sono intestazioni nella parte superiore degli intervalli X e Y.
- Scegli l’opzione di output preferita, un nuovo foglio di lavoro nel nostro caso.
- Facoltativamente, selezionare la casella di controllo Residui per ottenere la differenza tra i valori previsti e quelli effettivi.
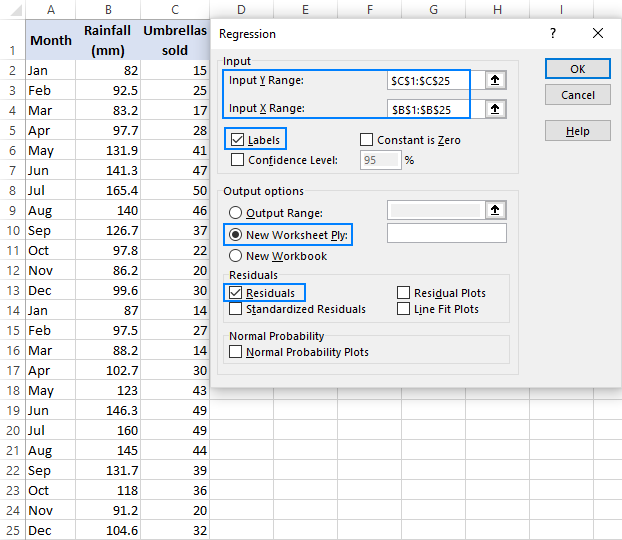
- Fare clic su OK e osservare l’output dell’analisi di regressione creato da Excel.
Interpretare l’output dell’analisi di regressione
Come hai appena visto, eseguire la regressione in Excel è facile perché tutti i calcoli sono preformati automaticamente. L’interpretazione dei risultati è un po ‘ più complicata perché è necessario sapere cosa c’è dietro ogni numero. Di seguito troverai una ripartizione di 4 parti principali dell’output dell’analisi di regressione.
Analisi di regressione output: Riepilogo Output
Questa parte ti dice quanto bene l’equazione di regressione lineare calcolata si adatta ai tuoi dati di origine.
Ecco cosa significa ogni informazione:
Multiple R. È il Coefficiente di correlazione che misura la forza di una relazione lineare tra due variabili. Il coefficiente di correlazione può essere qualsiasi valore compreso tra -1 e 1 e il suo valore assoluto indica la forza della relazione. Più grande è il valore assoluto, più forte è la relazione:
- 1 significa una forte relazione positiva
- -1 significa una forte relazione negativa
- 0 significa nessuna relazione
R Quadrato. È il Coefficiente di determinazione, che viene utilizzato come indicatore della bontà della vestibilità. Mostra quanti punti cadono sulla linea di regressione. Il valore R2 è calcolato dalla somma totale dei quadrati, più precisamente, è la somma delle deviazioni al quadrato dei dati originali dalla media.
Nel nostro esempio, R2 è 0,91 (arrotondato a 2 cifre), che è fatato. Significa che il 91% dei nostri valori si adatta al modello di analisi di regressione. In altre parole, il 91% delle variabili dipendenti (valori y) è spiegato dalle variabili indipendenti (valori x). Generalmente, R al quadrato del 95% o più è considerato una buona misura.
Rettificato R Quadrato. È il quadrato R regolato per il numero di variabili indipendenti nel modello. Si desidera utilizzare questo valore invece di R square per l’analisi di regressione multipla.
Errore standard. È un’altra misura di bontà che mostra la precisione della tua analisi di regressione: più piccolo è il numero, più puoi essere sicuro della tua equazione di regressione. Mentre R2 rappresenta la percentuale della varianza delle variabili dipendenti spiegata dal modello, l’errore standard è una misura assoluta che mostra la distanza media che i punti dati cadono dalla linea di regressione.
Osservazioni. È semplicemente il numero di osservazioni nel tuo modello.
l’analisi di Regressione di uscita: ANOVA
La seconda parte di questa produzione è l’Analisi della Varianza (ANOVA):
in sostanza, si divide la somma dei quadrati in singoli componenti che danno informazioni sui livelli di variabilità all’interno del vostro modello di regressione:
- df è il numero dei gradi di libertà associati con le fonti di varianza.
- SS è la somma dei quadrati. Più piccolo è il SS residuo rispetto al SS totale, migliore è il modello che si adatta ai dati.
- MS è il quadrato medio.
- F è la statistica F, o F-test per l’ipotesi nulla. Viene utilizzato per testare il significato complessivo del modello.
- Significato F è il valore P di F.
La parte ANOVA è raramente utilizzata per una semplice analisi di regressione lineare in Excel, ma dovresti assolutamente dare un’occhiata da vicino all’ultimo componente. Il valore Significance F dà un’idea di quanto siano affidabili (statisticamente significativi) i tuoi risultati. Se il significato F è inferiore a 0,05 (5%), il modello è OK. Se è maggiore di 0,05, probabilmente è meglio scegliere un’altra variabile indipendente.
Analisi di regressione output: coefficienti
Questa sezione fornisce informazioni specifiche sui componenti dell’analisi:
Il componente più utile in questa sezione sono i Coefficienti. Esso consente di costruire una equazione di regressione lineare in Excel:
Per il nostro set di dati, dove y è il numero di ombrelloni venduti e x è la media mensile delle precipitazioni, la nostra formula di regressione lineare va come segue:
Y = Rainfall Coefficient * x + Intercept
Dotato di a e b valori arrotondati a tre cifre decimali, si trasforma in:
Y=0.45*x-19.074
Ad esempio, con la piovosità media mensile pari a 82 mm, le vendite di ombrelli sarebbero circa 17,8:
0.45*82-19.074=17.8
In modo simile, è possibile scoprire quanti ombrelli saranno venduti con qualsiasi altra piovosità mensile (variabile x) specificata.
Analisi di regressione output: residuals
Se si confronta il numero stimato e effettivo di ombrelli venduti corrispondente alla pioggia mensile di 82 mm, si vedrà che questi numeri sono leggermente diversi:
- Stimato: 17.8 (calcolato sopra)
- Effettivo: 15 (riga 2 dei dati di origine)
Perché la differenza? Perché le variabili indipendenti non sono mai predittori perfetti delle variabili dipendenti. E i residui possono aiutarti a capire quanto sono lontani i valori effettivi dai valori previsti:
Come creare un grafico di regressione lineare in Excel
Se è necessario visualizzare rapidamente la relazione tra le due variabili, disegnare un grafico di regressione lineare. È molto facile! Ecco come:
- Seleziona le due colonne con i tuoi dati, incluse le intestazioni.
- Nella scheda Inset, nel gruppo Chat, fai clic sull’icona del grafico a dispersione e seleziona la miniatura a dispersione (la prima):
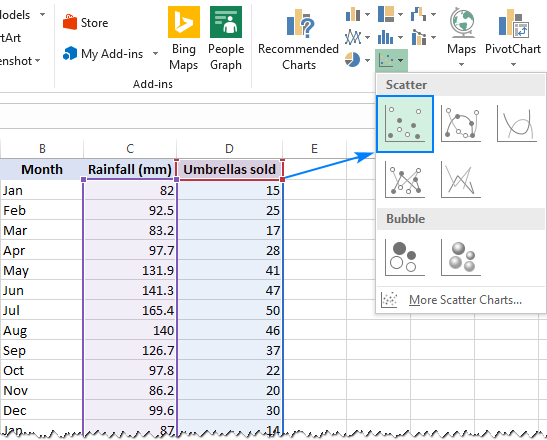
Questo inserirà un grafico a dispersione nel tuo foglio di lavoro, che assomiglierà a questo:
- Ora, dobbiamo disegnare il grafico linea di regressione dei minimi quadrati. Per averlo fatto, fare clic destro su qualsiasi punto e scegliere Aggiungi Trendline… dal menu contestuale.
- Nel riquadro di destra, selezionare la linea di tendenza Lineare forma e, facoltativamente, selezionare Visualizza l’Equazione sul Grafico per ottenere la vostra formula di regressione:
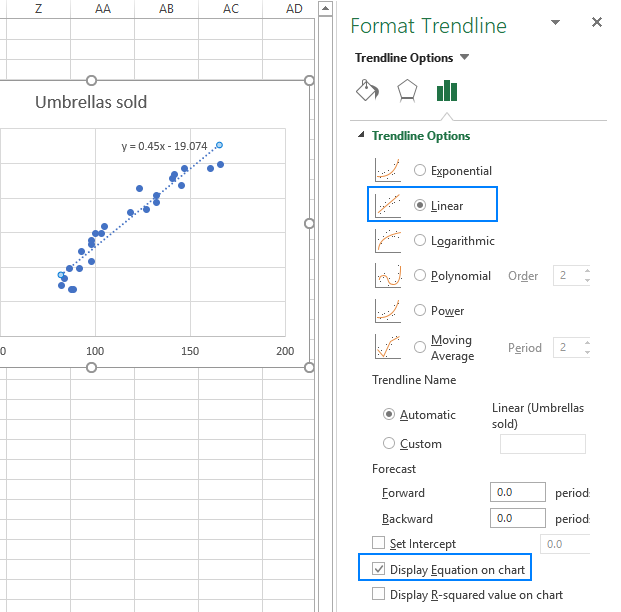
Come si può notare, l’equazione di regressione Excel ha creato per noi, come anche la formula di regressione lineare che abbiamo costruito sulla base dei Coefficienti di uscita.
- Passare alla scheda Linea Fill & e personalizzare la linea a proprio piacimento. Ad esempio, è possibile scegliere un diverso colore della linea e utilizzare una linea continua, invece di una linea tratteggiata (selezionare la linea continua nel Cruscotto tipo di casella):
A questo punto, il tuo grafico già sembra un decente regressione grafico:
Ancora, si consiglia di fare alcuni miglioramenti più:
- Trascinare l’equazione ovunque si vede in forma.
- Aggiungi titoli assi (Pulsante Elementi grafico > Titoli assi).
- Se i tuoi punti dati iniziano nel mezzo dell’asse orizzontale e/o verticale come in questo esempio, potresti voler eliminare lo spazio bianco eccessivo. Il seguente suggerimento spiega come eseguire questa operazione: Ridimensionare gli assi del grafico per ridurre lo spazio bianco.
Ed ecco come appare il nostro grafico di regressione migliorato:
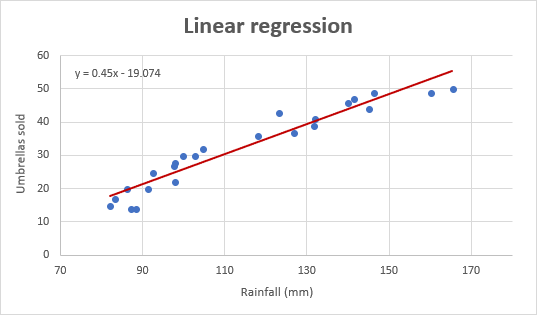Nota importante! Nel grafico di regressione, la variabile indipendente dovrebbe essere sempre sull’asse X e la variabile dipendente sull’asse Y. Se il tuo grafico è tracciato nell’ordine inverso, scambia le colonne nel tuo foglio di lavoro, quindi disegna di nuovo il grafico. Se non è consentito riorganizzare i dati di origine, è possibile cambiare gli assi X e Y direttamente in un grafico.
Come fare la regressione in Excel usando le formule
Microsoft Excel ha alcune funzioni statistiche che possono aiutarti a fare analisi di regressione lineare come LINEST, SLOPE, INTERCPET e CORREL.
La funzione LINEST utilizza il metodo di regressione dei minimi quadrati per calcolare una linea retta che spiega al meglio la relazione tra le variabili e restituisce un array che descrive quella linea. È possibile trovare la spiegazione dettagliata della sintassi della funzione in questo tutorial. Per ora, creiamo solo una formula per il nostro set di dati di esempio:
=LINEST(C2:C25, B2:B25)
Poiché la funzione LINEST restituisce un array di valori, è necessario inserirlo come formula di array. Selezionare due celle adiacenti nella stessa riga, E2:F2 nel nostro caso, digita la formula e premi Ctrl + Maiusc + Invio per completarla.
la formula restituisce Il b coefficiente (E1) e una costante (F1) per il già familiarità equazione di regressione lineare:
y = bx + a
Se si evitare l’uso di formule in forma di matrice in fogli di lavoro, è possibile calcolare a e b individualmente con regolare formule:
Ottenere l’intercetta di Y (a):
=INTERCEPT(C2:C25, B2:B25)
Ottenere la pendenza (b):
=SLOPE(C2:C25, B2:B25)
Inoltre, è possibile trovare il coefficiente di correlazione (R Multiple nell’analisi di regressione sintesi di uscita) che indica di quanto le due variabili sono correlate:
=CORREL(B2:B25,C2:C25)
La seguente schermata mostra tutte queste Excel formule di regressione in azione:
È così che fai la regressione lineare in Excel. Detto questo, si prega di tenere presente che Microsoft Excel non è un programma statistico. Se è necessario eseguire l’analisi di regressione a livello professionale, è possibile utilizzare software mirati come XLSTAT, RegressIt,ecc.
Download disponibili:
Per dare un’occhiata più da vicino alle nostre formule di regressione lineare e ad altre tecniche discusse in questo tutorial, puoi scaricare la nostra analisi di regressione di esempio nella cartella di lavoro di Excel.
- Come utilizzare Solver in Excel con esempi
- Come calcolare l’interesse composto in Excel
- Come calcolare CAGR (compound annual growth rate) in Excel
Leave a Reply