Energia di formazione del legame ionico

I legami ionici si formano quando gli ioni caricati positivamente e negativamente sono tenuti insieme da forze elettrostatiche. Considera una singola coppia di ioni, un catione e un anione. Quanto sarà forte la forza della loro attrazione? Secondo la Legge di Coulomb, l’energia dell’attrazione elettrostatica (\(E\)) tra due particelle cariche è proporzionale alla grandezza delle cariche e inversamente proporzionale alla distanza internucleare tra le particelle (\(r\)):

\

\

dove la carica di ogni ion è rappresentata dal simbolo Q. La costante di proporzionalità k è uguale a 2,31 × 10-28 J·m. Questo valore di k include la carica di un singolo elettrone (1,6022 × 10-19 C) per ogni ion. L’equazione può anche essere scritta usando la carica di ogni ion, espressa in coulombs (C), incorporata nella costante. In questo caso, la costante di proporzionalità, k, è uguale a 8,999 × 109 J * m / C2. Nell’esempio dato, Q1 = + 1(1,6022 × 10-19 C) e Q2 = -1 (1,6022 × 10-19 C). Se Q1 e Q2 hanno segni opposti (come in NaCl, ad esempio, dove Q1 è +1 per Na+ e Q2 è -1 per Cl−), allora E è negativo, il che significa che l’energia viene rilasciata quando gli ioni caricati in modo opposto vengono riuniti da una distanza infinita per formare una coppia di ioni isolati.

L’energia viene sempre rilasciata quando si forma un legame e, di conseguenza, richiede sempre energia per rompere un legame.

Come mostrato dalla curva verde nella metà inferiore della figura \(\PageIndex{1}\), l’energia massima verrebbe rilasciata quando gli ioni sono infinitamente vicini l’uno all’altro, a r = 0. Poiché gli ioni occupano spazio e hanno una struttura con il nucleo positivo circondato da elettroni, tuttavia, non possono essere infinitamente vicini tra loro. A distanze molto brevi, le interazioni repulsive elettrone-elettrone tra elettroni su ioni adiacenti diventano più forti delle interazioni attraenti tra ioni con cariche opposte, come mostrato dalla curva rossa nella metà superiore della figura \(\PageIndex{1}\). L’energia totale del sistema è un equilibrio tra le interazioni attraenti e repulsive. La curva viola in figura\ (\PageIndex{1}\) mostra che l’energia totale del sistema raggiunge un minimo a r0, il punto in cui le repulsioni elettrostatiche e le attrazioni sono esattamente bilanciate. Questa distanza è la stessa della distanza di legame misurata sperimentalmente.

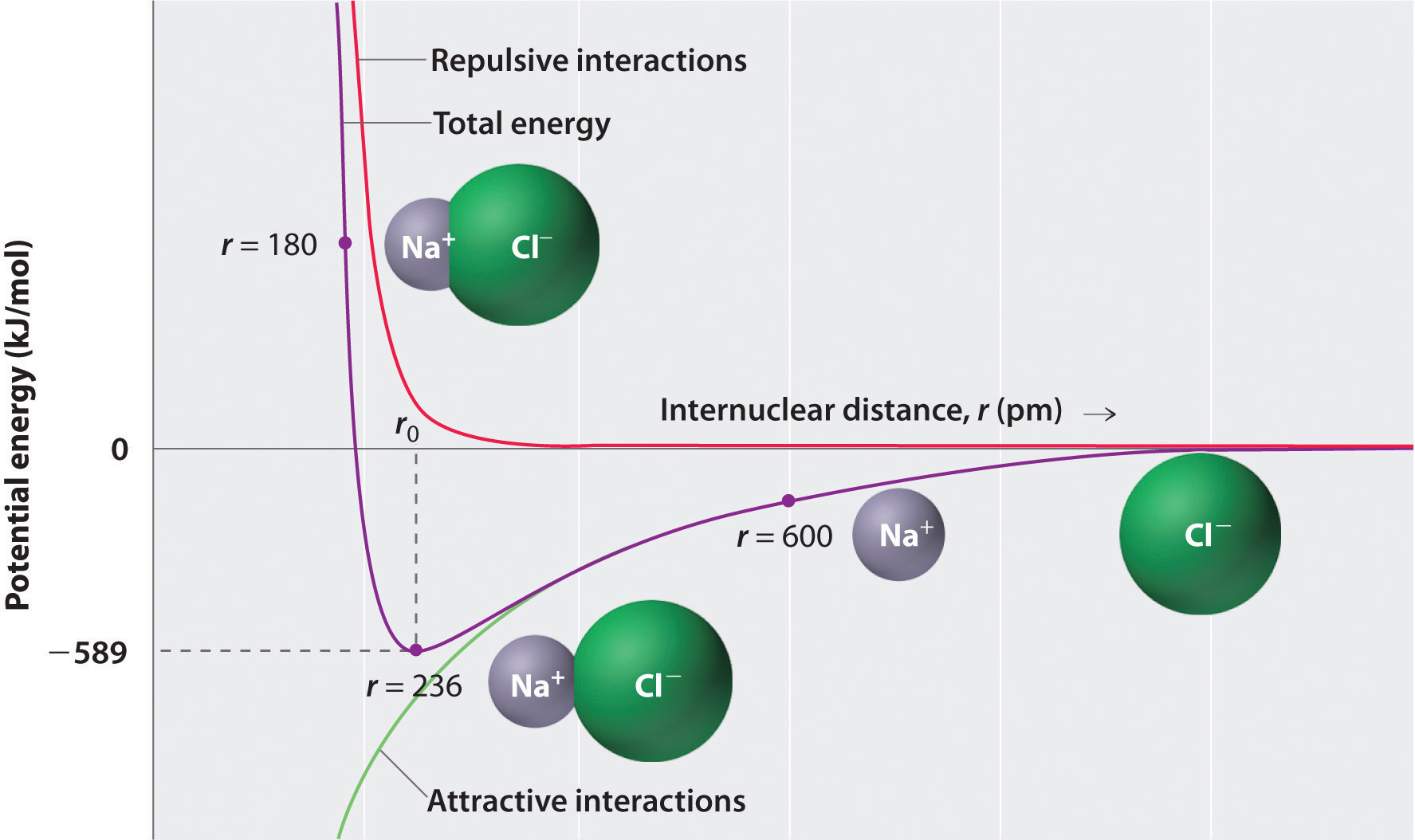
Considera l’energia rilasciata quando uno gas gassoso \(Na^+\) e uno gas gassoso \(Cl^-\) sono riuniti da r = ∞ a r = r0. Dato che l’osservato in fase gas internucleare distanza è di 236 pm, la variazione di energia associata con la formazione di una coppia di ioni da un \(Na^+_{(g)}\) ione e \(Cl^-_{(g)}\) ione è come indicato di seguito:

\ &= (2.31 \times {10^{ – 28}}\rm{J}\cdot \cancel{m} ) \left( \dfrac{( + 1)( – 1)}{236\; \annullare{pm} \times 10^{ – 12} \cancel{m/pm}} \right) \\ &= – 9.79\ volte 10^{ – 19}\; J/ion\; pair \ label{Eq2} \end{align*}\]

Il valore negativo indica che l’energia viene rilasciata. La nostra convenzione è che se un processo chimico fornisce energia al mondo esterno, il cambiamento energetico è negativo. Se richiede energia, il cambiamento energetico è positivo. Per calcolare il cambiamento di energia nella formazione di una mole di coppie NaCl, dobbiamo moltiplicare l’energia per coppia di ioni per il numero di Avogadro:

\

Questa è l’energia rilasciata quando si formano 1 mol di coppie di ioni gassosi, non quando 1 mol di ioni positivi e negativi si condensa per formare un reticolo cristallino. A causa delle interazioni a lungo raggio nella struttura reticolare, questa energia non corrisponde direttamente all’energia reticolare del solido cristallino. Tuttavia, il grande valore negativo indica che riunire ioni positivi e negativi è energeticamente molto favorevole, sia che si formi una coppia di ioni o un reticolo cristallino.

Riassumiamo i punti importanti sul legame ionico:

• A r0, gli ioni sono più stabili (hanno un’energia potenziale inferiore) di quanto non siano a una distanza internucleare infinita. Quando gli ioni caricati in modo opposto vengono riuniti da r = ∞ a r = r0, l’energia del sistema viene abbassata (l’energia viene rilasciata).
• A causa della bassa energia potenziale a r0, l’energia deve essere aggiunta al sistema per separare gli ioni. La quantità di energia necessaria è l’energia di legame.
• L’energia del sistema raggiunge un minimo ad una particolare distanza internucleare (la distanza di legame).