Interkvartilområder & Outliers
kvartiler & Bokser5-Nummeroversigt & Outliers
purplemath
“interkvartilområdet”, forkortet “IKR”, er kun bredden af kassen i kassen og Knurhårplottet. Det vil sige, IK = 3 .kvartal – 1. kvartal. IKR kan bruges som et mål for, hvor spredt værdierne er.
statistik antager, at dine værdier er grupperet omkring en central værdi. Det kan også bruges til at fortælle, hvornår nogle af de andre værdier er “for langt” fra den centrale værdi. Disse” for langt væk “punkter kaldes” outliers”, fordi de” ligger uden for ” det interval, hvor vi forventer dem.
ik er længden af kassen i din boks-and-knurhår plot. En outlier er en værdi, der ligger mere end en og en halv gange længden af kassen fra hver ende af kassen.
indhold fortsætter under
MathHelp.com
det vil sige, hvis et datapunkt er under 1.kvartal – 1,5. Måske stødte du på vejeskalaen, da du foretog den ene måling, eller måske er din laboratoriepartner en idiot, og du skulle aldrig have ladet ham røre ved noget af udstyret. Hvem ved? Men uanset deres årsag er outliers de punkter, der ikke synes at “passe”.
hvorfor en og en halv gange bredden af kassen for outliers? Hvorfor adskiller denne særlige værdi forskellen mellem” acceptable “og” uacceptable ” værdier? Fordi, da John Tukey opfandt kassen og knurhårplottet i 1977 for at vise disse værdier, valgte han 1,5. Dette har fungeret godt, så vi har fortsat med at bruge denne værdi lige siden. Hvis du går videre ind i statistikker, vil du opdage, at denne måling af rimelighed for klokkekurveformede data betyder, at normalt kun måske så meget som omkring en procent af dataene nogensinde vil være outliers.
Du kan bruge Matematikkontrollen nedenfor til at øve dig på at finde Interkvartilområdet, også kaldet “H-spredning” (eller spring kontrollen over og fortsæt med lektionen). Prøv den indtastede øvelse, eller skriv din egen øvelse. Klik derefter på knappen og rul ned til “Find Interkvartilområdet (H-spredning)” for at sammenligne dit svar med matematikens.
accepter venligst “præferencer” cookies for at aktivere denne kontrol.
(Klik på “tryk for at se trin”, der skal tages direkte til Matematikstedet for en betalt opgradering.)
Når du har det godt med at finde ik, kan du gå videre til at finde outliers, hvis nogen.
-
Find eventuelle afvigelser for følgende datasæt:
10.2, 14.1, 14.4. 14.4, 14.4, 14.5, 14.5, 14.6, 14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
for at finde ud af om der er nogen outliers, skal jeg først finde IKR. Der er femten datapunkter, så medianen vil være i ottende position:
(15 + 1) ÷ 2 = 8
derefter 2. kvartal = 14,6.
der er syv datapunkter på hver side af medianen. De to halvdele er:
10.2, 14.1, 14.4. 14, 4, 14, 4, 14, 5, 14, 5
…og:
14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
1. kvartal er den fjerde værdi på listen, idet den er den midterste værdi af den første halvdel af listen; og 3.kvartal er den tolvte værdi, idet den er den midterste værdi af anden halvdel af listen:
14,4
3 = 14,9
derefter gives IKR af:
IKR = 14,9 – 14,4 = 0,5
Outliers vil være et hvilket som helst punkt under 1. kvartal – 1,5 14,4 – 0,75 = 13,65 eller derover 3. kvartal + 1,5.
så er outliers på:
10.2, 15.9 og 16.4
Indholdet fortsætter under
værdierne for 1.kvartal – 1.5.5. hegnene er de” hegn”, der markerer de” rimelige ” værdier fra outlierværdierne. Outliers ligger uden for hegnene.
Hvis din opgave får dig til at overveje ikke kun outliers, men også “ekstreme værdier”, så er værdierne for 1.-1. 5. kvartal IK og 3. kvartal + 1. 5. kvartal ik de “indre” hegn, og værdierne for 1. -3. kvartal IK og 3. kvartal ik er de “ydre” hegn.
outliers (markeret med stjerner eller åbne prikker) er mellem de indre og ydre hegn, og de ekstreme værdier (markeret med det symbol, du ikke brugte til outliers) er uden for de ydre hegn.
forresten kan din bog henvise til værdien af ” 1,5. Derefter vil outliers være de tal, der er mellem et og to trin fra hængslerne, og ekstrem værdi vil være de tal, der er mere end to trin fra hængslerne.
når man ser igen på det foregående eksempel, ville de ydre hegn være på 14,4 – 3 liter 0,5 = 12,9 og 14,9 + 3 liter 0,5 = 16,4. Da 16.4 er lige på det øverste ydre hegn, ville dette kun betragtes som en outlier, ikke en ekstrem værdi. Men 10.2 er helt under det nedre ydre hegn, så 10.2 ville være en ekstrem værdi.
Affiliate
Affiliate
din grafregner kan muligvis ikke angive, om en boks-og-knurhårplot inkluderer outliers. Ovenstående problem omfatter f.eks. punkterne 10.2, 15.9 og 16.4 som afvigende. En indstilling på min grafregner giver den enkle boks-og-knurhårplot, der kun bruger fem-nummeroversigten, så de fjerneste outliers vises som værende endepunkterne for knurhårene:

en anden regnemaskine indstilling giver boksen-og-knurhår plot med outliers specielt markeret (i dette tilfælde, med en simulering af en åben prik), og knurhår går kun så langt som de højeste og laveste værdier, der ikke outliers:

min lommeregner skelner ikke mellem outliers og ekstreme værdier. Din måske ikke, enten. Tjek din brugervejledning nu, før den næste test.
Hvis du bruger din grafregner til at hjælpe med disse plot, skal du sørge for at vide, hvilken indstilling du skal bruge, og hvad resultaterne betyder, eller lommeregneren kan give dig et helt korrekt, men “forkert” svar.
-
Find eventuelle outliers og ekstreme værdier for følgende datasæt, og tegn felt-og-knurhår-plottet. Marker eventuelle outliers med en stjerne og eventuelle ekstreme værdier med en åben prik.
21, 23, 24, 25, 29, 33, 49
annonce
for at finde outliers og ekstreme værdier skal jeg først finde ICR. Da der er syv værdier på listen, er medianen den fjerde værdi, så:
KV2 = 25
den første halvdel af listen er:
21, 23, 24
…så KV1 = 23; den anden halvdel er:
29, 33, 49
…så 3.kvartal = 33. Derefter gives ik ‘ en af:33 – 23 = 10
outliers vil være nogen værdier nedenfor:
23 – 1.5×10 = 23 – 15 = 8
…eller over:
33 + 1.5×10 = 33 + 15 = 48
de ekstreme værdier vil være dem nedenfor:
23 – 3×10 = 23 – 30 = -7
…eller over:
33 + 3×10 = 33 + 30 = 63
så jeg har en outlier på 49, men ingen ekstreme værdier. Jeg vil ikke have en top knurhår på mit plot, fordi 3.kvartal også er den højeste ikke-outlier. Så mit plot ser sådan ud:
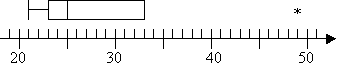
det skal bemærkes, at de metoder, vilkår og regler, der er skitseret ovenfor, er det, jeg har lært, og hvad jeg oftest har set undervist. Dit kursus kan dog have forskellige specifikke regler, eller din lommeregner kan foretage beregninger lidt anderledes. Du skal muligvis være lidt fleksibel med at finde de svar, der er specifikke for din læseplan.
URL: https://www.purplemath.com/modules/boxwhisk3.htm
side 1side 2side 3
Leave a Reply