Fibonacci-sekvens
Fibonacci-sekvensen er rækken af tal:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
det næste tal findes ved at tilføje de to tal før det:
- 2 findes ved at tilføje de to tal før det (1+1),
- 3 findes ved at tilføje de to tal før det (1+2),
- 5 er (2+3),
- og så videre!
eksempel: det næste tal i sekvensen ovenfor er 21+34 = 55
det er så simpelt!
Her er en længere liste:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
kan du finde ud af de næste par tal?
laver en Spiral
når vi laver firkanter med disse bredder, får vi en dejlig spiral:
kan du se, hvordan firkanterne passer pænt sammen?
for eksempel 5 og 8 gør 13, 8 og 13 gør 21 osv.

denne spiral findes i naturen!
Se: Natur, Det gyldne forhold og Fibonacci
reglen
Fibonacci-sekvensen kan skrives som en “regel” (se sekvenser og serier).
for det første er vilkårene nummereret fra 0 og fremefter som denne:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
så term nummer 6 kaldes H6 (hvilket svarer til 8).
|
Eksempel: 8. term er H8 = H7 + H6 |
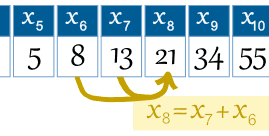 |
så vi kan skrive reglen:
reglen er HN = HN−1 + HN−2
hvor:
- n “
- HN−1 er det foregående udtryk (n−1)
- HN−2 er udtrykket før det (n−2)
eksempel: term 9 beregnes således:
Golden Ratio
og her er en overraskelse. Når vi tager to på hinanden følgende (den ene efter den anden) Fibonacci-tal, er deres forhold meget tæt på det gyldne forhold “prisT”, som er cirka 1.618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
Vi behøver ikke at starte med 2 og 3, her valgte jeg tilfældigt 192 og 16 (og fik sekvensen 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
det tager længere tid at få gode værdier, men det viser, at ikke kun Fibonacci-sekvensen kan gøre dette!
brug af det gyldne forhold til at beregne Fibonacci − tal
og endnu mere overraskende er, at vi kan beregne ethvert Fibonacci−tal ved hjælp af det gyldne forhold:
HN = lartn – (1 – -) n-5
svaret kommer ud som et helt tal, nøjagtigt lig med tilføjelsen af de to foregående udtryk.
eksempel: H6
H6 = (1.618034…)6 − (1−1.618034…) 6 liter 5
da jeg brugte en lommeregner på dette (kun indtastning af det gyldne forhold til 6 decimaler) fik jeg svaret 8.00000033 , en mere præcis beregning ville være tættere på 8.
prøv n=12 Og se hvad du får.
Du kan også beregne et Fibonacci-tal ved at multiplicere det forrige Fibonacci-tal med det gyldne forhold og derefter afrunding (fungerer for tal over 1):
Eksempel: 8 liter = 8 liter 1.618034… = 12.94427… = 13 (afrundet)
nogle interessante ting
Her er Fibonacci-sekvensen igen:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Der er et interessant mønster:
- se på nummeret H3 = 2. Hvert 3. nummer er et multiplum af 2 (2, 8, 34, 144, 610, …)
- se på tallet H4 = 3. Hver 4. nummer er et multiplum af 3 (3, 21, 144,…)
- se på tallet 5 = 5. Hver 5. nummer er et multiplum af 5 (5, 55, 610,…)
og så videre (hvert nth tal er et multiplum af NN).
1 / 89 = 0, 011235955056179775…
Bemærk de første få cifre (0,1,1,2,3,5) er Fibonacci-sekvensen?
På en måde er de alle, undtagen flere cifrede tal (13, 21 osv) overlapper hinanden, som dette:
… osv …
0, 011235955056179775… = 1/89
vilkår under nul
sekvensen fungerer også under nul, som denne:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(bevis for dig selv, at hvert nummer findes ved at tilføje de to tal før det!)
faktisk har sekvensen under nul de samme tal som sekvensen over nul, bortset fra at de følger a +-+- … mønster. Det kan skrives som dette:
h−n = (-1)n+1 H
som siger, at udtrykket” – n “er lig med (-1)n+1 gange udtrykket “n”, og værdien (-1)n+1 gør det rigtige +1, -1, +1, -1, … mønster.
historie
Fibonacci var ikke den første til at vide om sekvensen, den var kendt i Indien hundreder af år før!

om Fibonacci manden
hans rigtige navn var Leonardo Pisano Bogollo, og han boede mellem 1170 og 1250 i Italien.”Fibonacci “var hans kaldenavn, som stort set betyder”søn af Bonacci”.
ud over at være berømt for Fibonacci-sekvensen hjalp han med at sprede Hindu-arabiske tal (som vores nuværende tal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) gennem Europa i stedet for romertal (I, II, III, IV, V osv.). Det har sparet os alle en masse problemer! Tak Leonardo.



Leave a Reply